3.3.7. Пошукові методи оптимізації технічних об’єктів та систем

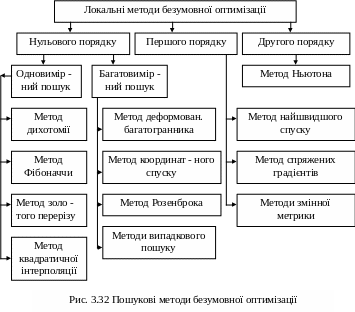
Найбільш часто, особливо для складних систем, застосовують пошукові методи оптимізації. В залежності від типа екстремуму розрізняють методи локальної і глобальної, умовної і безумовної оптимізації. Останні є найбільш чисельними (рис. 3.32). В залежності від порядку похідних цільової функції за керованими параметрами, які використовуються для пошуку екстремуму, методи безумовної оптимізації поділяють на методи нульового, першого і другого порядку.

В методах нульового порядку (прямі методи) похідна не використовується; в методах першого порядку обчислюють як функцію, так і перші часткові похідні (градієнтні методи); в методах другого порядку, окрім функції визначають перші і другі її похідні.

В залежності від кількості керованих параметрів розрізняють методи одновимірного та багатовимірного пошуку.

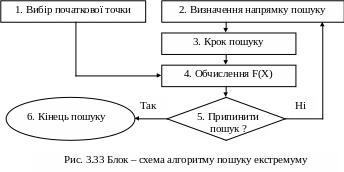
Всі методи оптимізації спрямовані знайти таку послідовність керованих параметрів Х₀, Х₁, Х₂,… і т. д. , при якій F(X₀) > F(X₁) > F(X₂) >……. при пошуку мінімуму F(X) i F(X₀) < F(X₁) < F(X₂) <……. при пошуку максимуму F(X) . В такому випадку забезпечується збіжність і екстремум може бути знайдений. Схема алгоритму пошуку наведена на рис. 3.33.

Початкова точка Х₀ повинна належати області визначення і , за можливості, знаходитися якомога ближче до екстремуму. Сутність конкретного метода оптимізації визначається етапами 2 і 3, де отримують координати чергової точки Х_к+1 на траєкторії пошуку. Після обчислення цільової функції в цій точці F(X_k+1) роблять висновки щодо досягнення екстремуму або щодо необхідності продовження пошуку.

Методи одновимірного пошуку розподіляються на методи послідовного пошуку (методи дихотомії, Фібоначчі, золотого перерізу) і методи з апроксимацією функції (квадратичної і кубічної інтерполяції, метод Піявського і т. д.).

З методів послідовного пошуку метод дихотомії (половинного ділення) є найбільш простим.

Якщо на к – тому кроці виконуються два досліди, то аргументи х_{1, к} і х_{2, к} повинні вибиратися на відстані справа і зліва від середини інтервалу:

; ,

де δ > 0 – константа, яка визначає відстань між двома значеннями аргументу;

а_к і в_к – межі інтервалу на к – тому кроці.

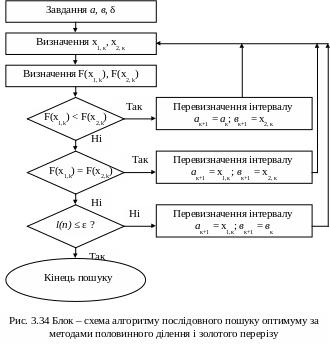
Після визначення F(X_{1, k}) i F(X_{2, k}) знаходять інтервал невизначеності. Для пошуку мінімуму:

• якщо F(X_{1, k}) < F(X_{2, k}), то а_к+1 = а_к ; в_к+1 = х_{2, к};

• якщо F(X_{1, k}) = F(X_{2, k}), то а_к+1 = х_1,к ; в_к+1 = х_{2, к};

• якщо F(X_{1, k}) > F(X_{2, k}), то а_к+1 = х_1,к ; в_к+1 = в_к

Потім знову обчислюють координати х₁ та х₂ і продовжують пошук. Після n експериментів (n – парне число) екстремум буде обмежений інтервалом довжиною:

,

де (в – а) – інтервал на початку пошуку.

В методі золотого перерізу експерименти X_{1, k} i X_{2, k} визначають з урахуванням коефіцієнту пропорційності τ = 0,382:

Х_{1, к} = а_к + 0,382(в_к – а_к); Х_{2, к} = в_к - 0,382(в_к – а_к).

В цих точках визначають цільову функцію F(X), аналізують інтервал невизначеності і продовжують пошук.

На рис. 3.34 наведена блок – схема алгоритмів половинного ділення та золотого переріза.

Послідовність пошуку екстремуму (мінімуму) за найбільш розповсюдженим з методів оптимізації з апроксимацією функції – методом квадратичної інтерполяції є наступною.

Етап 1. Обчислення F(x) в початковій точці х₀.

Етап 2. Призначення кроку h. Якщо F(x₀ +h) < F(x₀), переходять до етапу 3; якщо F(x₀ +h) ≥ F(x₀), приймають h = - h і виконують етап 3.

Етап 3. Обчислення х_к+1 = х_к + h і F(x_k+1).

Етап 4. Якщо F(x_к+1) ≤ F(x_к), то крок h подвоюють і виконують етап 3. Якщо F(x_к+1) > F(x_к), то х_к+1 позначають через х_m, х_к – через х_{m – 1}, зменшують h наполовину і етап 3 виконують в останній раз.

Етап 5. Виключення з отриманих чотирьох значень х_{m + 1}, х_m, х_{m - 1}, х_{m - 2} які знаходяться на однаковій відстані одне від одного, або х_{m + 1}, або х_{m - 2} в залежності від того, яка з цих точок знаходиться на більшій відстані від точки х, в якій функція F(х) має найменше значення.

Припустимо, х_а, х_в, х_с – точки, що залишилися; х_с – центральна з цих точок, а х_а = х_с – h; х_в = х_с + h.

Етап 6. Проведення квадратичної інтерполяції для визначення координати екстремуму:

.

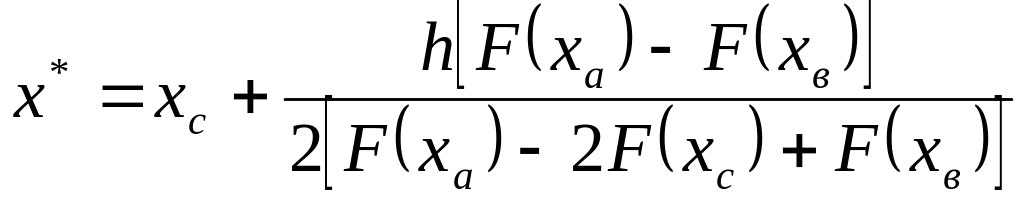Блок – схема алгоритму наведена на рис. 3.35.

Проілюструємо процедуру пошуку оптимуму за розглянутими методами.

Приклад. Знайти оптимальний коефіцієнт витрати повітря х для однозонної печі, який забезпечує мінімальну витрату полива F на її опалення за експериментально отриманою моделлю:

F = 1200 – 1320х + 600х², .

Пошук виконати за методами дихотомії, золотого перерізу, квадратичної інтерполяції і зіставити його результати з даними аналітичного рішення. Початковий діапазон варіювання х обмежений значеннями 0,6 за умови утворення кіптявого факелу і 2,0 за умови забезпечення стабілізації процесу горіння.

Рішення. а) Пошук за методом половинного ділення.

Приймаємо рекомендовані границі інтервалу х на першому кроці а₁ = 0,6; в₁ = 2,0; відстань між двома значеннями х: δ = 0,02.

Дослідні точки на першому кроці і значення цільової функції в них:

; ;

F(x_1,1) = 1200 – 1320x_1,1+ 600x_1,1² = 1200 – 1320*1,29 + 600*1,29² = 95,66 ;

F(x_2,1) = 1200 – 1320x_2,1+ 600x_2,1² = 1200 – 1320*1,31 + 600*1,31² =500,46 .

Оскільки F(x_1,1) < F(x_2,1), то на другому кроці приймаємо:

а₂ = а₁ = 0,6; в₂ = х_2,1 = 1,31; ;

;

F(x_1,2) = 1200 – 1320x_1,2+ 600x_1,2² = 1200 – 1320*0,945 + 600*0,945² = 488,415 ; F(x_2,2) = 1200 – 1320x_2,2+ 600x_2,2² = 1200 – 1320*0,965 + 600*0,965² = 484,935 .

Враховуючи, що F(x_1,2) > F(x_2,2), приймаємо: а₃ = х_1,2 = 0,945; в₃ = в₂ = 1,31 і виконуємо третій крок пошуку.

Дослідні точки при цьому і значення цільової функції в них наступні:

; ; F(x_1,3) = 1200 – 1320x_1,3+ 600x_1,3² = 1200 – 1320*1,1175 + 600*1,1175² = 474,181 ; F(x_2,3) = 1200 – 1320x_2,3+ 600x_2,3² = 1200 – 1320*1,1375 + 600*1,1375² = 474,84 .

Оскільки значення цільової функції F(x_1,3) наближено дорівнює її величині в точці x_2,3, можна прийняти х^* як середнє з кінцевого діапазону:

.

Витрата полива на піч за таким х^* складе:

F = 1200 – 1320x^* + 600(x^*)² = 1200 – 1320*1,1275 + 600*1,1275² = 474,5 .

Це значення є декілька більшим, ніж отримане в точці х_1,3, тому більш доцільно остаточно прийняти х^* = х_1,3 = 1,1175, де значення F становить 474,181 .

б) Пошук за методом золотого перерізу.

Приймемо границі інтервалу х на першому кроці попередніми: а₁ = 0,6; в₁ = 2,0. Координати дослідних точок і значення цільової функції в них на першому кроці:

х_1,1 = а₁ + 0,382(в₁ - а₁) = 0,6 + 0,382(2,0 – 0,6) = 1,1348;

х_2,1 = в₁ - 0,382(в₁ - а₁) = 2,0 - 0,382(2,0 – 0,6) = 1,4652;

F(x_1,1) = 1200 – 1320x_1,1+ 600x_1,1² = 1200 – 1320*1,1348 + 600*1,1348² = 474,7266 ;

F(x_2,1) = 1200 – 1320x_2,1+ 600x_2,1² = 1200 – 1320*1,4652 + 600*1,4652² = 554,0226 .

Оскільки F(x_1,1) < F(x_2,1), то границі інтервалу на другому кроці приймаємо:

а₂ = а₁ = 0,6; в₂ = х_2,1 = 1,4652.

Дослідні точки на другому кроці і значення F в них:

х_1,2 = 0,6 + 0,382(1,4652 – 0,6) = 0,9305;

х_2,2 = 1,4652 - 0,382(1,4652 – 0,6) = 1,1347;

F(x_1,2) = 1200 – 1320x_1,2+ 600x_1,2² = 1200 – 1320*0,9305 + 600*0,9305² = 491,2382 ;

F(x_2,2) = 1200 – 1320x_2,2+ 600x_2,2² = 1200 – 1320*1,1347 + 600*1,1347² = 474,7225 .

З огляду на дотримання нерівності F(x_1,2) > F(x_2,2), приймаємо для третього кроку: а₃ = х_1,2 = 0,9305; в₃ = в₂ = 1,4652, обчислюємо координати дослідних точок і величини цільової функції в них:

х_1,3 = а₃ + 0,382(в₃ – а₃) = 0,9305 + 0,382(1,4652 – 0,9305) = 1,1348;

х_2,3 = в₃ - 0,382(в₃ – а₃) = 1,4652 - 0,382(1,4652 – 0,9306) = 1,2609;

F(x_1,3) = 1200 – 1320x_1,3+ 600x_1,3² = 1200 – 1320*1,1348 + 600*1,1348² = 474,7266 ;

F(x_2,3) = 1200 – 1320x_2,3+ 600x_2,3² = 1200 – 1320*1,2609 + 600*1,2609² = 489,5333 .

Для четвертого кроку приймаємо: а₄ = а₃ = 0,9305; в₄ = х_2,3 = 1,2609, оскільки F(x_1,.3) < F(x_2,3).

х_1,4 = а₄ + 0,382(в₄ – а₄) = 0,9305 + 0,382(1,2609 – 0,9305) = 1,0567;

х_2,4 = в₄ - 0,382(в₄ – а₄) = 1,2609 - 0,382(1,2609 – 0,9306) = 1,1135;

F(x_1,4) = 1200 – 1320x_1,4+ 600x_1,4² = 1200 – 1320*1,0567 + 600*1,0567² = 475,125 ;

F(x_2,4) = 1200 – 1320x_2,4+ 600x_2,4² = 1200 – 1320*1,1135 + 600*1,1135² = 474,11 .

Наближено значення F(x_1,4) і F(x_2,4) дорівнюють одне одному, тому припиняємо пошук і визначаємо х^*.

Якщо прийняти: , то значення цільової функції становить:

F(x^*) = 1200 – 1320x^*+ 600(x^*)² = 1200 – 1320*1,0851 + 600*1,0851² = 474,2 .

З наведених раніш міркувань приймаємо х^* = х_2,4 = 1,1135, де F приймає значення 474,11 .

в) Пошук за методом квадратичної інтерполяції.

Початкову точку приймаємо посередині припустимого інтервалу варіювання:

.

Величину кроку залишимо базовою: h = δ = 0,02.

Значення цільової функції в початковій точці:

F(x₀) = 1200 – 1320x₀+ 600x₀² = 1200 – 1320*1,3 + 600*1,3² = 498 .

Координата наступної точки і значення цільової функції в ній:

х₁ = х₀ + h = 1,3 + 0,02 = 1,32;

F(x₁) = 1200 – 1320x₁+ 600x₁² = 1200 – 1320*1,32 + 600*1,32² = 503,04 .

Оскільки F(x₀) < F(x₁), змінюємо напрям руху на протилежний шляхом нового визначення кроку і координат точки на траєкторії пошуку:

h₁ = - h = - 0,02; х₁ = х₀ - h = 1,3 - 0,02 = 1,28;

F(x₁) = 1200 – 1320*1,28 + 600*1,28² = 493,44 .

Враховуючи, що знайдене F(x₁) = 493,44 < F(x₀) = 498 , приймаємо подвоєний крок у вибраному напрямку, знаходимо координату точки траєкторії і величину цільової функції в ній:

h₂ = 2h₁ = 2(- 0,02) = - 0.04; х₂ = х₁ + h₂ = 1,28 - 0,04 = 1,24;

F(x₂) = 1200 – 1320x₂+ 600x₂² = 1200 – 1320*1,24 + 600*1,24² = 485,76 .

Зважаючи на нерівність F(x₂) < F(x₁), продовжуємо рух у тому ж напрямку:

х₃ = х₂ + h₂ = 1,24 - 0,04 = 1,20;

F(x₃) = 1200 – 1320x₃+ 600x₃² = 1200 – 1320*1,20 + 600*1,20² = 485,76 .

Аналогічно виконуються наступні крокі в напрямку оптимуму:

• F(x₃) < F(x₂);

х₄ = х₃ + h₂ = 1,20 - 0,04 = 1,16;

F(x₄) = 1200 – 1320*1,16 + 600*1,16² = 476,16 ;

- F(x₄) < F(x₃);

х₅ = х₄ + h₂ = 1,16 - 0,04 = 1,12;

F(x₅) = 1200 – 1320*1,12 + 600*1,12² = 474,24 ;

- F(x₅) < F(x₄);

х₆ = х₅ + h₂ = 1,12 - 0,04 = 1,08;

F(x₆) = 1200 – 1320*1,08 + 600*1,08² = 474,24 ;

- F(x₆) = F(x₅);

х₇ = х₆ + h₂ = 1,08 - 0,04 = 1,04;

F(x₇) = 1200 – 1320*1,04 + 600*1,04² = 476,16 .

Оскільки F(x₆) < F(x₇), приймаємо половинний крок і в останній раз обчислюємо координату нової точки і значення цільової функції в ній:

h₃ = 0,5h₂ = 0,5(- 0,04) = - 0,02; х₈ = х₇ + h₃ = 1,04 - 0,02 = 1,02;

F(x₈) = 1200 – 1320*1,02 + 600*1,02² = 477,84 .

Порівняємо останні чотири значення F(x):

F(x₅) = 474,24 ; F(x₆) = 474,24 ; F(x₇) = 476,16 ;

F(x₈) = 477,84 .

Найбільшим з них є F(x₈), тому відкидаємо цю точку. Для розрахунку координати оптимуму приймаємо в якості центральної точки х₆, а крайніх – х₅ та х₇. За формулою квадратичної інтерполяції отримуємо:

;

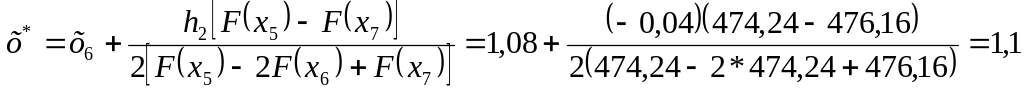F(x^*) = 1200 – 1320x^*+ 600(x^*)² = 1200 – 1320*1,1 + 600*1,1² = 474 .

Для аналітичного рішення застосуємо необхідні та достатні умови існування екстремуму, оскільки ця елементарна функція може бути двічі диференційована:

, звідки знаходимо х^* = 1,1.

> 0, що свідчить про досягнення мінімуму в точці х^*.

Значення цільової функції в цій точці:

F(x^*) = 1200 – 1320*1,1 + 600*1,1² = 474 ,

що відповідає знайденим пошуковими методами значенням.

Великий клас складають методи багатовимірного пошуку оптимуму.

Координатний метод Гауса – Зайделя і його розвиток метод Пауела включає здійснення послідовних одновимірних пошуків, починаючи з деякої початкової точки Х_0,0 (рис. 3.36).

В цій точці початковий напрямок руху S_1,0 ,….., S_n,0 вибирають паралельно координатним осям х₁,…., х_n, причому першим здійснюється рух уздовж n – ної осі n – вимірного простору. Для функції F(x₁, x₂) двох координат на рис. 3.36 спочатку напрямок S_2,0 вибирають уздовж вісі х₂, а потім S_1,0 уздовж х₁ .

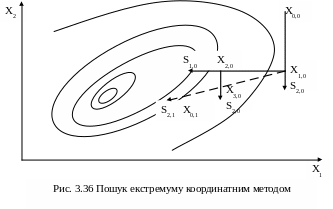
За методом Гауса - Зайделя почергово змінюють кожну вхідну змінну до досягнення часткового оптимуму. Спочатку досягається частковий оптимум у напрямку однієї координатної вісі х_і при фіксованих значеннях інших факторів. Потім стабілізують знайдене значення параметру х_і і починають змінювати інший фактор, по якому знову досягають часткового оптимуму і т. д.

Мінімізація або максимізація F(X_0,0 + hS_n,0) по h у вибраному напрямку виконується за допомогою якогось методу одновимірного оптимального пошуку і знайдений оптимальний крок дозволяє перейти в точку Х_1,0 = Х_0,0 + hS_n,0. Потім уздовж кожного з n напрямків ця процедура повторюється. Визначенням координат точки Х_{n +1, 0} ( для двохвимірного випадку точку Х_3,0) закінчується попередній етап пошуку і починається аналогічний наступний.

На відмінність від методу Гауса – Зайделя, який характеризується великою тривалістю пошуку, в методі Пауела потім виконується одновимірний пошук уздовж напрямку S_2,1 = (Х_3,0 – Х_1,0) за пунктирною лінією. В новій точці Х_0,1 знову приймається напрямок S_n,0 і пошук продовжується за описаною процедурою. Закінчення пошуку після завершення (n – 1) етапів здійснюється в тому випадку, коли зміна за кожною незалежною змінною стає менш, ніж задана точність ε.

Метод деформованого багатогранника Нелдера та Міда є модифікацією симплексного метода. Симплексом називають регулярний багатогранник в n – вимірному евклідовому просторі. Для двох змінних – це рівнобічний трикутник; для трьох змінних – це тетраедр. Тобто в n – вимірному просторі симплекс має (n + 1) вершину. Координати вершин вихідного симплекса можуть визначатися двома способами:

1. За допомогою матриці R розміром n × (n + 1)

,

де r₁ = ;

r₂ = ;

l – відстань між вершинами симплекса.

Для двох факторів (рис. 3.37) маємо: r₁ = 0,966l; r₂ = 0,259l .

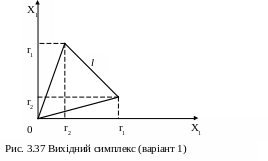
2. За допомогою матриці:

де r_j = ; R_j = ; j = 1, 2, 3,….., n

n – кількість параметрів.

Центр симплекса при цьому розміщений в центрі координат; вершина (n + 1) на вісі Х_n ,а інші вершини розташовані симетрично відносно вісі Х_n . Наприклад, для двох факторів маємо:

r₁ = =0,5; R₁ = ; r₂ = = 0,289;

R₂ = = 0,578.

Побудований за даними табл. 3.1 план вихідного симплекса за цім способом наведений на рис. 3.38.

Таблиця 3.1

Безрозмірні координати вихідного симплекса

№№ дослідів	Х1	Х2
1	- 0,5	- 0,289
2	+ 0,5	- 0,289
3	0	+ 0,578

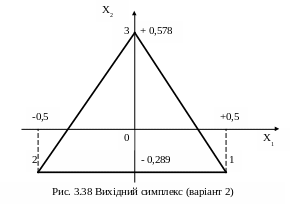
Пошук мінімуму (максимуму) цільової функції виконується наступним чином. Визначають координати вершин симплекса і обчислюють в них значення цільової функції F(Х). Знаходять вершину з найгіршим для даної задачі значенням F(Х). Через цю вершину і центральну точку симплекса проводять пряму, на ній на деякий відстані від центру встановлюють нову вершину, а вершина, де спостерігалося найгірше значення F(Х), відкидається. Таким чином, новий симплекс будується на залишених і одній новій вершині.

На рис. 3.39 показаний процес пошуку оптимуму, коли здійснюється послідовна заміна найгіршої точки 1 в симплексі 1 2 3 на точку 4 з утворенням нового симплекса 2 3 4. Якщо в ньому найгіршою стає точка 2 , то вона замінюється своїм дзеркальним відображенням відносно протилежної грані 3 4 (точка 5) з побудовою нового симплекса 3 4 5. Подальший рух здійснюється шляхом відкидання найгірших точок 3, 5, 4, 6, 8 і послідовної заміни їх на точки 6, 7, 8, 9, 10 з побудовою нових симплексів.

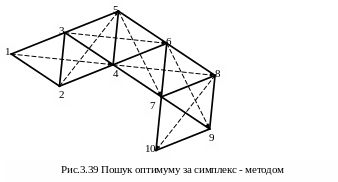
Але при використанні жорсткого симплекса з досягненням області екстремуму спостерігається “ зациклення” процесу пошуку, коли при заміні най гіршої точки в попередньому симплексі на нову величина цільової функції в ній знову стає найгіршою. В таких умовах звичайно доводиться припиняти пошук.

В методі Нелдера і Міда координати вершин базового (початкового) симплексу визначають з матриці R, а на наступних етапах конфігурація симплекса змінюється: над ним можуть виконуватися операції відображення, як і для жорсткого симплексу; розтягу; стиску; редукції (рис. 3.40).

Позначимо Х_jк ( j = 1, 2, …., n +1) j – ту вершину (точку) на к – тому етапі пошуку оптимуму функції F(Х). Припустимо, що вершина Х_к^А характеризується максимальним значенням F(Х), найгіршим для пошуку мінімуму, а вершина Х_к^В – мінімальним, тобто найкращим. Вектор координат центру багатогранника Х_к^С має елементи:

,

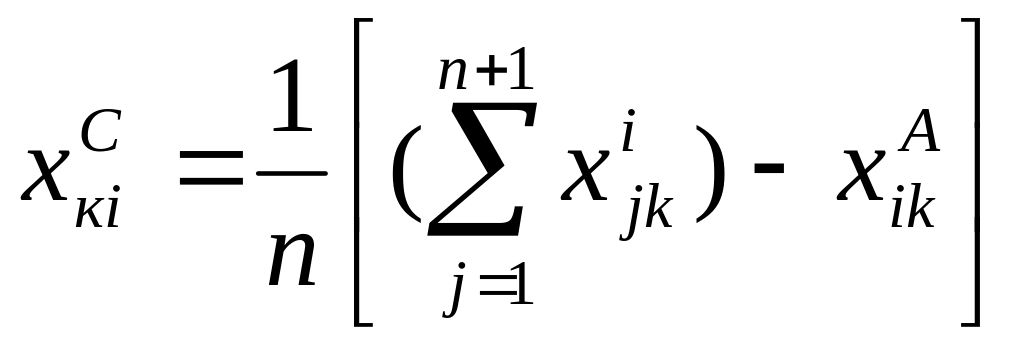де і = 1, 2, …, n – номер координати;

х_ік^А – і – та координата вершини з максимальним значенням F(Х) на к – тому етапі пошуку.

Операція відображення – це проектування Х_к^А через центр зі співвідношення:

Х_{n+2, к} = Х_к^С + α(Х_к^С – Х_к^А),

де α > 0 – коефіцієнт відображення; звичайно α = 1.

Розтяг використовують, якщо відображення виявилося вдалим, тобто, коли для пошуку мінімуму F(X_{n+2, k}) < F(X^B _k) . Координати нової вершини визначають зі співвідношення:

Х_{n+3, к} = Х_к^С + γ(Х_{n+2, k} – Х_к^C),

де γ – коефіцієнт розтягу.

Вектор (Х_{n+2, k} – Х_к^C) тут розтягується, оскільки звичайно приймають γ = 2,8 – 3,0.

Стиск виконується, якщо в результаті відображення F(X_{n+2, k}) стало більшим, ніж решта вершин. Вектор (Х_к^А – Х_к^С) стискають за співвідношенням:

Х_{n+4, к} = Х_к^С + β(Х^А _k – Х_к^C),

де 0 < β < 1 – коефіцієнт стиску, який звичайно вибирають на рівні 0,4 – 0,6.

Редукція – це стиск симплексу в 2 рази. Цю операцію застосовують при F(X_{n+2, k}) > F(X^А _k) і виконують за співвідношенням:

Х_{j, к} = Х_к^B + 0,5(Х _j,k – Х_к^B),

де j = 1, 2, ….., n + 1.

Умовою припинення пошуку є виконання співвідношення:

,

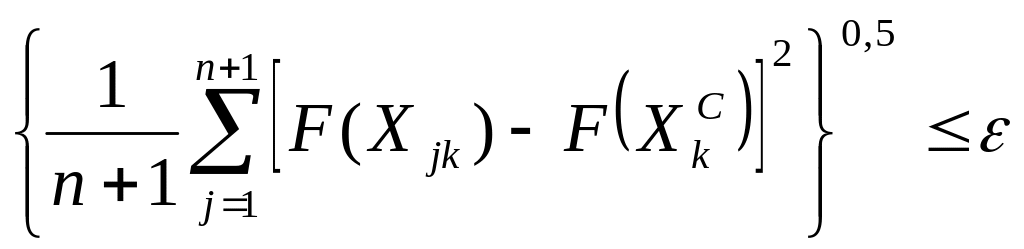де ε > 0 – мале число, яке визначає ε – околицю екстремуму.

Алгоритм методу передбачає наступні етапи.

1. Визначення координат вершин початкового симплексу та значень цільової функції F(Х) в них.

2. Визначення вершини з найбільшим та найменшим значенням F(Х) і координат центру симплекса Х_к^С.

3. Виконання операції відображення: пошук координат Х_{n+2, к} відображеної вершини і значення функції F(X_{n+2, k}) в ній.

4.За умови F(X_{n+2, k}) > F(X^B _k) при пошуку мінімуму переходять до п. 7.

5. Виконання операції розтягу з визначенням координат Х_{n+3, к} і значення F(X_{n+3, k}) .

6. За умови F(X_{n+3, k}) < F(X^B _k) приймають Х_к^А = Х_{n+3, к}; за умови F(X_{n+3, k}) ≥ F(X^B _k) приймають Х_к^А = Х_{n+2, к} і переходять до п. 12.

7. Перевірка умови F(X_{n+2, k}) > F(X_{j, k}) для всіх j ≠ A. При невиконанні цієї нерівності приймають Х_к^А = Х_{n+2, к} і пошук продовжують за п. 12.

8. Якщо F(X_{n+2, k}) ≥ F(X^А _k) , приймають Х_к^А = Х_{n+2, к} ; за умови F(X_{n+2, k}) < F(X^А _k) приймають Х_к^А = Х_к^А .

9. Виконання операції стиску з обчисленням координати Х_{n+4, к} та значення функції F(X_{n+4, k}).

10. За умови F(X_{n+4, k}) ≤ F(X^А _k) приймають Х_к^А = Х_{n+4, к} і переходять до п. 12.

11. Виконання редукції симплекса.

12. За умови пошук припиняють. В разі невиконання цієї умови індекс етапу пошуку К збільшують на одиницю, тобто визначають К як К+1, і пошук мінімуму повторюють з п. 2.

Проілюструємо використання симплекс – методу та метода Гауса – Зайделя для пошуку оптимуму.

Приклад. Визначити оптимальні коефіцієнти витрати повітря z₁ та z₂ на спалювання палива в зонах двозонної печі, які забезпечують мінімальну витрату палива F на піч. Пошук здійснити за допомогою симплекс - метода, метода Гауса – Зайделя і порівняти результати з даними аналітичного рішення.

Цільова функція має вигляд:

F = 3500 – 2400z₁ – 1500z₂ + 600z₁² + 375z₂² + 300z₁z₂ , .

Початкові значення та інтервали варіювання керованих параметрів прийняти z_1,0 = z_2,0 = 1,0; h₁ = h₂ = 0,2.

Рішення. а) Пошук за симплекс – методом.

Координати вершин вихідного симплексу визначаємо за другим варіантом побудови матриці, який був наведений раніш, коли центр симплекса розміщений в точці початку координат. Величини керованих параметрів в натуральному масштабі визначаємо за формулами кодування:

z_j,i = z_j,0 + x_j,ih_j ,

де і = 1, 2, …, n + 1 – номери дослідів.

Використовуємо безрозмірні значення х_1,і та х_2,і з вихідної матриці і отримуємо:

- для досліду і = 1: z_1,1 = z_1,0 + x_1,1h₁ = 1,0 – 0,2*0,5 = 0,9;

z_2,1 = z_2,0 + x_2,1h₂ = 1,0 – 0,2*0,289 = 0,9422;

- для досліду і = 2: z_1,2 = z_1,0 + x_1,2h₁ = 1,0 + 0,2*0,5 = 1,1;

z_2,2 = z_2,0 + x_2,2h₂ = 1,0 – 0,2*0,289 = 0,9422;

- для досліду і = 3: z_1,3 = z_1,0 + x_1,3h₁ = 1,0 + 0,2*0 = 1,0;

z_2,3 = z_2,0 + x_2,3h₂ = 1,0 + 0,2*0,578 = 1,1156.

Значення цільової функції у вихідній серії дослідів:

F₁ = 3500 – 2400z_1,1 – 1500z_2,1 + 600z_1,1² + 375z_2,1² + 300z_1,1z_2,1 = 3500 – 2400*0,9 – 1500*0,9422 + 600*0,9² + 375*0,9422² + 300*0,9*0,9422 = 1020,4 ;

F₂ = 3500 – 2400z_1,2 – 1500z_2,2 + 600z_1,2² + 375z_2,2² + 300z_1,2z_2,2 = 3500 – 2400*1,1 – 1500*0,9422 + 600*1,1² + 375*0,9422² + 300*1,1*0,9422 = 836,9 ;

F₃ = 3500 – 2400z_1,3 – 1500z_2,3 + 600z_1,3² + 375z_2,3² + 300z_1,3z_2,3 = 3500 – 2400*1,0 – 1500*1,1156 + 600*1,0² + 375*1,1156² + 300*1,0*1,1156 = 828 .

За результатами вихідної серії дослідів замінюємо точку 1, в якій максимальна витрата палива, на її дзеркальне відображення відносно центра протилежної грані симплекса 2 - 3. Координати нової точки 4 визначаємо за формулою:

,

де z_j,l та z_j,n+2 – j – та координата найгіршої і нової точки; і ≠ l.

; .

Значення цільової функції в цій точці:

F₄ = 3500 – 2400z_1,4 – 1500z_2,4 + 600z_1,4² + 375z_2,4² + 300z_1,4z_2,4 = 3500 – 2400*1,2 – 1500*1,1156 + 600*1,2² + 375*1,1156² + 300*1,2*1,1156 = 678,9 .

В новому симплексі, який утворений точками 2, 3, 4, найгіршою є точка 2. Тому замінюємо її новою точкою 5 з координатами:

; .

Витрата палива на опалення печі при таких коефіцієнтах витрати повітря становить:

F₅ = 3500 – 2400z_1,5 – 1500z_2,5 + 600z_1,5² + 375z_2,5² + 300z_1,5z_2,5 = 3500 – 2400*1,1 – 1500*1,289 + 600*1,1² + 375*1,289² + 300*1,1*1,289 = 701 .

Аналогічно виконуємо наступні кроки до оптимуму:

• крок 3 (заміна точки 3 на точку 6)

; ;

F₆ = 3500 – 2400*1,3 – 1500*1,289 + 600*1,3² + 375*1,289² + 300*1,3*1,289 = 586,3 ;

- крок 4 (заміна точки 5 на точку 7)

; ;

F₇ = 3500 – 2400*1,4 – 1500*1,1156 + 600*1,4² + 375*1,1156² + 300*1,4*1,1156 = 577,9 ;

• крок 5 (заміна точки 4 на точку 8)

; ;

F₈ = 3500 – 2400*1,5 – 1500*1,289 + 600*1,5² + 375*1,289² + 300*1,5*1,289 = 519,7 ;

• крок 6 (заміна точки 6 на точку 9)

; ;

F₉ = 3500 – 2400*1,6 – 1500*1,1156 + 600*1,6² + 375*1,1156² + 300*1,6*1,1156 = 524,8 ;

• крок 7 (заміна точки 7 на точку 10)

; ;

F₁₀ = 3500 – 2400*1,7 – 1500*1,289 + 600*1,7² + 375*1,289² + 300*1,7*1,289 = 501 ;

• крок 8 (заміна точки 9 на точку 11)

; ;

F₁₁ = 3500 – 2400*1,6 – 1500*1,4624 + 600*1,6² + 375*1,4624² + 300*1,6*1,4624 = 506,4 ;

• крок 9 (заміна точки 8 на точку 12)

; ;

F₁₂ = 3500 – 2400*1,8 – 1500*1,4624 + 600*1,8² + 375*1,4624² + 300*1,8*1,4624 = 522,1 .

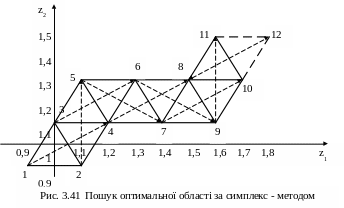
Оскільки після заміни точки 8 нова точка 12 знову стає найгіршою, то можна зробити висновок, що область екстремуму досягнута і обмежена точками 9, 10, 11. Оптимальні значення z₁ та z₂ знаходяться в межах 1,5 ÷ 1,7 і 1,289 ÷ 1,4624 відповідно. В табл. 3.2 зведені результати пошукових рухів, а рис. 3.41 наведена графічна інтерпретація руху до оптимуму за симплекс - методом.

Таблиця 3.2

Результати пошуку оптимальної області за симплекс - методом

№№ дослідів	z1	z2	F,
1	0,9	0,9422	1020,4
2	1,1	0,9422	836,9
3	1,0	1,1156	828,0
4	1,2	1,1156	678,9
5	1,1	1,289	701,0
6	1,3	1,289	586,3
7	1,4	1,1156	577,9
8	1,5	1,289	519,7
9	1,6	1,1156	524,8
10	1,7	1,289	501,0
11	1,6	1,4624	506,4
12	1,8	1,4624	522,1

б) Пошук оптимуму за методом Гауса – Зайделя.

Рух розпочинаємо уздовж вісі z₂ з початкової точки z_2,0 = 1,0 зі сталим кроком h₂ = 0,2 при фіксованому значенні z_1,0 = 1,0. Цільова функція при цьому має вигляд:

F₁ = 3500 – 2400*1 – 1500z₂ + 600*1² + 375z₂² + 300*1*z₂ = 1700 – 1200z₂ + 375z₂² , .

ЇЇ значення в початковій точці:

F₁(z_2,0) = 1700 – 1200z_2,0 + 375z_2,0² = 1700 – 1200*1 + 375*1² = 875 .

Координата z₂ після першого кроку пошуку і значення цільової функції:

z_2,1 = z_2,0 + h₂ = 1,0 + 0,2 = 1,2; F₁(z_2,1) = 1700 – 1200z_2,1 + 375z_2,1² = 1700 – 1200*1,2 + 375*1,2² = 800 .

Оскільки F₁(z_2,0) > F₁(z_2,1), то координата z₂ на другому кроці і величина F₁ становлять:

z_2,2 = z_2,1 + h₂ = 1,2 + 0,2 = 1,4; F₁(z_2,2) = 1700 – 1200z_2,2 + 375z_2,2² = 1700 – 1200*1,4 + 375*1,4² = 755 .

Аналогічно на третьому кроці, оскільки F₁(z_2,1) > F₁(z_2,2), отримуємо:

z_2,3 = z_2,2 + h₂ = 1,4 + 0,2 = 1,6; F₁(z_2,3) = 1700 – 1200z_2,3 + 375z_2,3² = 1700 – 1200*1,6 + 375*1,6² = 740 .

Зважаючи на нерівність F₁(z_2,2) > F₁(z_2,3), робимо наступний крок у тому ж напрямку:

z_2,4 = z_2,3 + h₂ = 1,6 + 0,2 = 1,8; F₁(z_2,4) = 1700 – 1200z_2,4 + 375z_2,4² = 1700 – 1200*1,8 + 375*1,8² = 755 .

Нерівність F₁(z_2,4) > F₁(z_2,3) свідчить про досягнення локального оптимуму за координатою z₂; для оцінки координати оптимуму z₂^* використаємо формулу квадратичної інтерполяції, причому приймемо в якості розрахункових рівновіддалені точки z_2,2, z_2,3, z_2,4 :

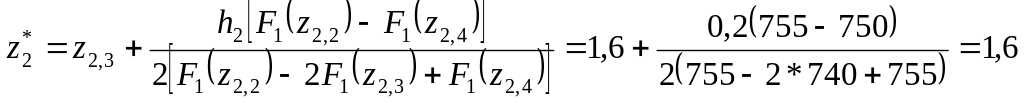
На другому етапі здійснюємо спуск за координатою z₁ при сталому значенні z₂ = z₂^* = 1,6; вид цільової функції при русі за цією координатою буде наступний:

F₂ = 3500 – 2400z₁ – 1500*1,6 + 600z₁² + 375*1,6² + 300z₁*1,6 = 2060 – 1920z₁ + 600z₁² ,

В початковій точці руху в цьому напрямку (z_1,0 = 1,0; z₂^* = 1,6) величина цільової функції складає:

F₂(z_1,0) = 2060 – 1920z_1,0 + 600z_1,0² = 2060 – 1920*1,0 + 600*1,0² = 740 .

Після першого кроку координата z₁ і значення цільової функції становлять:

z_1,1 = z_1,0 + h₁ = 1,0 + 0,2 = 1,2; F₂(z_1,1) = 2060 – 1920*1,2 + 600*1,2² = 620 .

Оскільки F₂(z_1,0) > F₂(z_1,1), зберігаємо вибраний напрямок руху:

z_1,2 = z_1,1 + h₁ = 1,2 + 0,2 = 1,4; F₂(z_1,2) = 2060 – 1920*1,4 + 600*1,4² = 548 .

Аналогічно виконуємо третій крок (F₂(z_1,1) > F₂(z_1,2)):

z_1,3 = z_1,2 + h₁ = 1,4 + 0,2 = 1,6; F₂(z_1,3) = 2060 – 1920*1,6 + 600*1,6² = 524

і четвертий (F₂(z_1,2) > F₂(z_1,3)):

z_1,4 = z_1,3 + h₁ = 1,6 + 0,2 = 1,8; F₂(z_1,4) = 2060 – 1920*1,8 + 600*1,8² = 548 .

З огляду на нерівність F₂(z_1,4) > F₂(z_1,3), проводимо квадратичну інтерполяцію, причому приймаємо граничними розрахункові точки z_1,2 і z_1,4 , які рівновіддалені від центральної точки z_1,3 з мінімальним значенням F₂. Координата локального екстремуму:

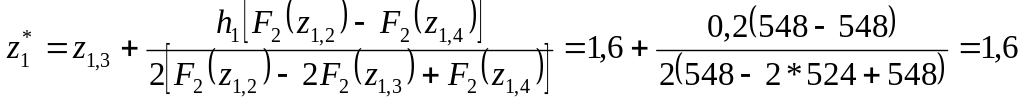
На наступному етапі здійснюємо пошук за координатою z₂ з початкової точки z_2,0 = 1,6 при сталому значенні z₁ = z₁^* =1,6; цільова функція при цьому має вигляд:

F₃ = 3500 – 2400*1,6 – 1500z₂ + 600*1,6² + 375z₂² + 300*1,6*z₂ = 1196 – 1020z₂ + 375z₂² ,

В початковій точці цього руху значення цільової функції складає:

F₃(z_2.0) = 1196 – 1020*1,6 + 375*1,6² = 524 .

На першому кроці координата z₂ і цільова функція F₃ мають наступні значення:

z_2,1 = z_2,0 + h₂ = 1,6 + 0,2 = 1,8; F₃(z_2,1) = 1196 – 1020*1,8 + 375*1,8² = 575 .

Оскільки F₃(z_2,1) > F₃(z_2,0), треба змінити напрямок руху на протилежний, тобто прийняти h₂ = - 0,2:

z_2,1 = z_2,0 + h₂ = 1,6 - 0,2 = 1,4; F₃(z_2,1) = 1196 – 1020*1,4 + 375*1,4² = 503 .

З огляду на нерівність F₃(z_2,0) > F₃(z_2,1), розраховуємо z_2,2 і F₃(z_2,2) :

z_2,2 = z_2,1 + h₂ = 1,4 - 0,2 = 1,2; F₃(z_2,2) = 1196 – 1020*1,2 + 375*1,2² = 512 .

Оскільки точками z_2,0 = 1,6; z_2,1 = 1,4; z_2,2 = 1,2 обмежена область локального екстремуму (F₃(z_2,0) > F₃(z_2,1); F₃(z_2,2) > F₃(z_2,1)), квадратичною інтерполяцією знаходимо оптимальне значення z₂^*:

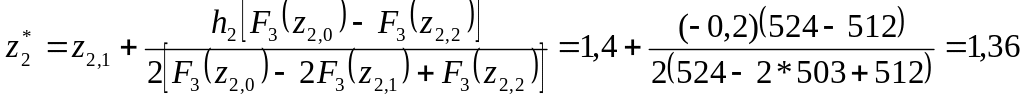
Починаємо спуск за координатою z₁ з початкової точки z₁ = 1,6 при сталому значенні z₂ = z₂^* = 1,36; цільова функція при цьому набуває вигляд:

F₄ = 3500 – 2400z₁ – 1500*1,36 + 600z₁² + 375*1,36² + 300z₁*1,36 = 2153,6 – 1992z₁ + 600z₁² ,

В початковій точці:

z_1,0 = 1,6; F₄(z_1,0) = 2153,6 – 1992*1,6 + 600*1,6² = 502,4 .

На першому кроці пошуку:

z_1,1 = z_1,0 + h₁ = 1,6 + 0,2 =1,8; F₄(z_1,1) =2153,6 – 1992*1,8 + 600*1,8² =512 .

Оскільки F₄(z_1,0) виявилося менш, ніж F₄(z_1,1), змінюємо напрямок пошуку і приймаємо h₁ = - 0,2:

z_1,1^/ = z_1,0 + h₁ = 1,6 - 0,2 = 1,4;

F₄(z_1,1^/ ) = 2153,6 – 1992*1,4 + 600*1,4² = 540,8 .

З огляду на те, що і цьому напрямку не вдалося досягнути зменшення цільової функції відносно її значення в початковій точці, виконуємо інтерполяцію, причому в якості центральної приймаємо початкову точку:

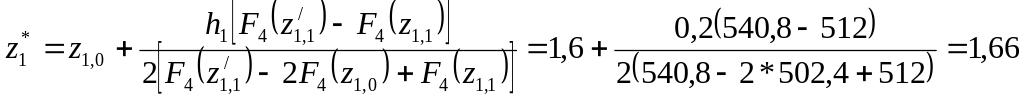
Виконуємо наступний етап пошуку за координатою z₂ з початкової точки z_2,0 = 1,36 при z₁ = z₁^* = 1,66 = idem; цільова функція при цьому буде:

F₅ = 3500 – 2400*1,66 – 1500z₂ + 600*1,66² + 375z₂² + 300*1,66*z₂ = 1169,4 – 1002z₂ + 375z₂² , ,

і її значення в початковій точці:

F₅(z_2,0) = 1169,4 – 1002*1,36 + 375*1,36² = 500,3 .

На першому кроці:

z_2,1 = z_2,0 + h₂ = 1,36 + 0,2 = 1,56;

F₅(z_2,1) = 1169,4 – 1002*1,56 + 375*1,56² = 518,9

Оскільки F₅(z_2,1) > F₅(z_2,0), приймаємо h₂ = - 0,2 і обчислюємо значення:

z_2,1^/ = z_2,0 + h₂ = 1,36 - 0,2 = 1,16;

F₅(z_2,1^/) = 1169,4 – 1002*1,16 + 375*1,16² = 511,7 .

З огляду на нерівність F₅(z_2,1^/) > F₅(z_2,0), переходимо до квадратичної інтерполяції:

Зниження ефективності пошуку екстремуму за координатою z₂ до і за координатою z₁ до , що менш, ніж 5%, свідчить про доцільність його припинення і прийняття координат оптимуму z₁^* = 1,336; z₂^* = 1,66. На рис. 3.42 наведена траєкторія руху до оптимуму за цім методом.

в) Аналітичне визначення оптимуму.

Знайдемо перші часткові похідні цільової функції за керованими параметрами, прирівняємо їх нулю і отримаємо координати точки екстремуму:

;

;

4z₁ + z₂ = 8;

z₁ + 2,5z₂ = 5;

z₁^* = 1,667; z₂^* = 1,333

Другі похідні функції:

; ;

Матриця других похідних, її кутовий мінор і визначник гесиану:

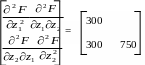
Δ₁ = 1200 > 0; Δ = 120*750 – 300*300 > 0.

Тобто, маємо мінімум функції. Отримані пошуковими методами оптимальні значення z₁ i z₂ з урахуванням вибраної точності відповідають результатам аналітичного рішення.

Звичайно, застосовувати пошукові методи, якщо є можливість вирішити задачу аналітично, особливо в найпростіших випадках, як у наведених вище прикладах, не має сенсу. Ці приклади дані лише для детального роз’яснення процедури пошуку екстремуму з допомогою методів одно – та багатовимірної оптимізації.

Сутність методів випадкового пошуку полягає у випадковому виборі напрямку руху на кожному наступному кроці. В цих методах використовують випадковий вектор, який має однакову можливість приймати різні напрямки. Для його формування використовують випадкові числа.

Простішим з цих методів є метод сліпого пошуку або метод Монте – Карло. В ньому на наступному (К+ 1) – шому кроці пошуку з припустимої області вибирають випадкову точку Х_к+1 , визначають в ній цільову функцію F(X_k+1) і порівнюють її зі значенням, яке отримано на попередньому кроці F(X_k). Якщо при пошуку мінімуму F(X_k+1) < F(X _k), то координати нової точки і нове значення цільової функції запам’ятовується замість Х_к і F(X_k). В разі невиконання цієї нерівності роблять спробу досягнути успіху шляхом зміни напрямку на протилежний або вибором нового випадкового напрямку. Координати нової точки знаходять зі співвідношення:

Х_к+1 = Х_к + hS_k .

Випадковий напрямок руху S_k знаходять за допомогою випадкового вектора S = (s₁, s₂, …, s_n), компонентами якого є випадкові величини, які рівномірно розподілені в інтервалі [- 1; + 1].

Градієнтні методи відносяться до групи методів оптимізації першого порядку. Оптимум шукають в напрямку найбільш швидкого зростання або зниження вихідної змінної об’єкту. Перед виконанням кроку пошуку у напрямку градієнта функції спочатку виконують його розрахунок за відомою моделлю:

,

де - часткові похідні цільової функції за факторами х₁, х₂, …., х_n ;

i, j,…, n – одиночні вектори (орти) в напрямку координатних осів.

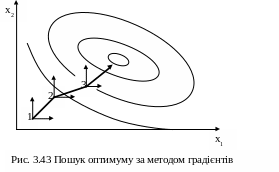
В разі відсутності такої моделі градієнт знаходять за результатами спробних рухів у напрямку координатних осів (рис. 3.43).

Напрямок градієнта відповідає напрямку найшвидшого зростання цільової функції. Стратегія пошуку будується на визначенні координати наступної точки з виразу:

Х_к+1 = Х_к + hS_k ,

де h – величина кроку;

S_k – одиничний вектор напрямку пошуку на К – тому кроці.

Спосіб вибору кроку h і напрямку S_k визначає сутність конкретного методу. При пошуку мінімуму треба рухатися у напрямку, протилежному градієнту F(X). Зі співвідношення:

S_k =

можна отримати формулу для переходу від Х_к до Х_к+1:

Х_к+1 = Х_к - h ,

де ║ F(X_k)║ - норма вектора градієнта на К – тому кроці пошуку.

Тобто за методом градієнтів кожна j – та координата на (К + 1) – шому кроці визначається з формули:

, j = 1, 2, …, n.

Оскільки при виході до “майже стаціонарної” області (до області екстремуму ) величина знижується, то крок пошуку зменшується, що призводить до зростання часу пошуку.

В методі найшвидшого спуску, який є розвитком методу градієнтів, рух з оптимальним кроком розраховують за допомогою одновимірної мінімізації цільової функції по h уздовж напрямку, протилежному градієнту. Алгоритм цього методу полягає в наступному.

1. Визначають всі часткові похідні цільової функції за керованими параметрами у вихідній або проміжних точках.

2. Знаходять одним з методів одновимірного пошуку оптимальний крок уздовж напрямку, протилежно градієнту. Величину h визначають з умови мінімуму функції за h, тобто .

3. Визначають координати нової точки:

Х_к+1 = Х_к - h .

4.Якщо умови припинення пошуку не виконуються, повертаються до п. 1.

Траєкторія пошуку за цім методом показана на рис.3.44.

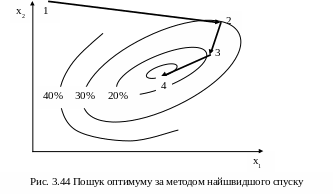
Рух уздовж одного напрямку припиняється, коли лінія напрямку пошуку стає дотичною до якоїсь лінії однакового рівня.

Багато у чому аналогічним до цього методу є метод крутого сходження або метод Бокса – Уілсона. Слід зауважити, що будь – який метод оптимізації дозволяє досягнути оптимуму. Однак ефективність конкретного методу визначається часом, необхідним для його досягнення. Для ілюстрації цього порівняємо ефективність пошуку оптимуму градієнтним методом і методом найшвидшого спуску.

Приклад. В системі здійснюється пошук екстремуму вихідного параметра у шляхом зміни управління u на її вході (рис. 3.45).

Система включає об’єкт управління, який описується рівняннями:

; φ = К₂(х₁² + х₂²)

і виконавчі пристрої, математична модель динаміки яких має вигляд:

; .

Приймемо параметри системи: Т = 20с; К₁ = 1; К₁ = 1; К₂ = 0,8; К₃ = К₄ = 0,01 ; максимально припустиме відхилення від точки екстремуму в кінці пошуку Δу = 0,4кПа; початкові умови: х₁₀ = 2кПа; х₂₀ = 1кПа при τ = 0.

а) пошук за методом градієнтів.

Управління u є пропорційним проекціям градієнту:

; .

Оскільки рух здійснюється в бік зниження градієнту, то диференційні рівняння виконавчих пристроїв приймають вигляд:

; .

Знак “ – “ тут означає, що рух до мінімуму здійснюється у напрямку вектора градієнта. Шляхом інтегрування отримуємо:

; lnx₁ = - 2K₂K₃τ + C₁; х₁ = С ехр( - 2К₂К₃τ).

Сталу інтегрування знаходимо з початкових умов:

х₁ = х₁₀ при τ = 0; х₁₀ = С ехр( - 2К₂К₃*0) = С; х₁ = х₁₀ ехр( - 2К₂К₃τ).

Шляхом аналогічних перетворень отримуємо:

х₂ = х₂₀ ехр( - 2К₂К₄τ).

Тоді диференційне рівняння об’єкту прийме вигляд:

.

Отримане неоднорідне диференційне рівняння вирішуємо методом невизначених множників. Відповідне однорідне рівняння має вигляд:

і його рішення:

,

де А(τ) – невизначений множник.

Знайдемо похідну функції і підставимо знайдені у та в неоднорідне рівняння:

; ;

;

=

Враховуючи, що , отримуємо:

.

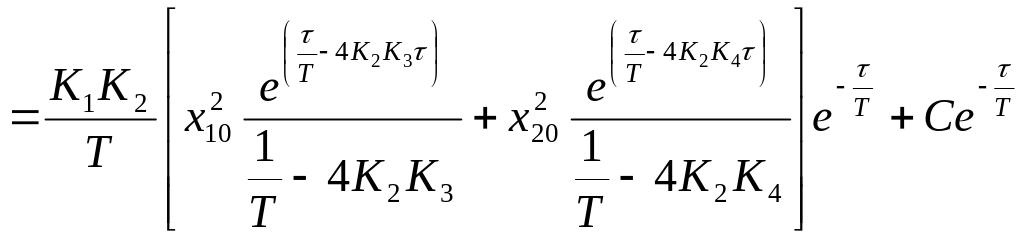
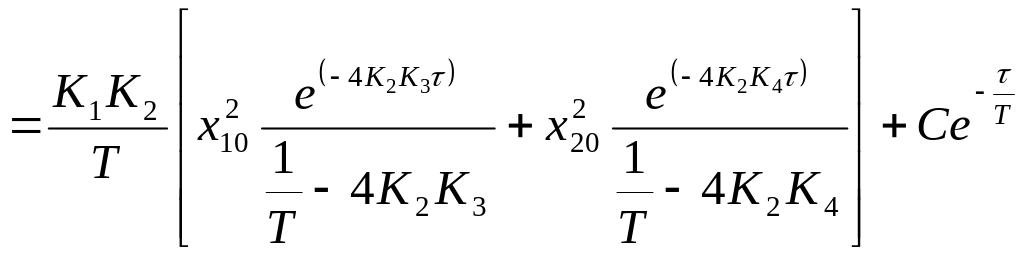Сталу інтегрування С визначаємо з початкових умов:

;

.

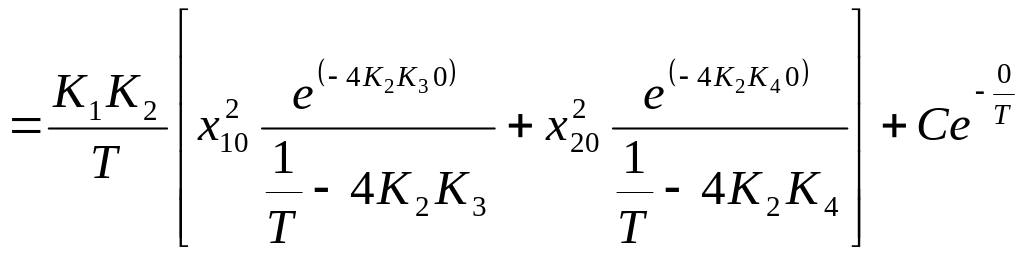В початковому стаціонарному стані при τ = 0 і у₀ = К₁φ =К₁К₂(х₁₀² + х₂₀²), тобто вихідна величина повністю визначається координатами х₁₀ та х₂₀.

Тоді рішення диференційного рівняння прийме вигляд:

.

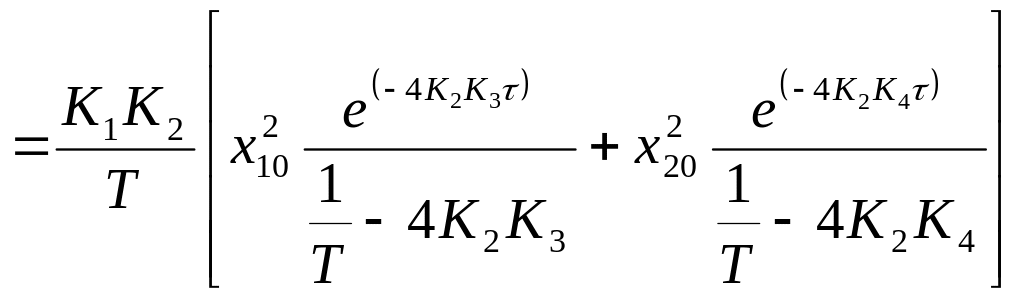
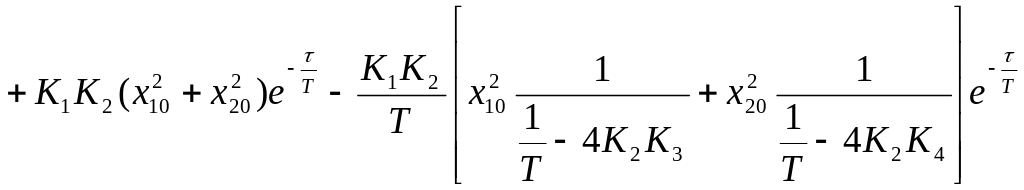Після підстановки числових значень параметрів отримуємо:

у(τ) = 11,111е ^{– 0,032τ} – 7,111е ^{– 0,05τ}.

Підставимо в це рівняння час τ = 80; 90; 100; 101с і знайдемо відповідні значення у(80) = 0,7287; у(90) = 0,5447; у(100) = 0,4050; у(101) = 0,3931. Тобто тривалість пошуку за методом градієнтів складає приблизно 100,5с.

б) пошук за методом найшвидшого спуску.

Рух за координатами х₁ та х₂ здійснюється зі сталою швидкістю, яка дорівнює значенню градієнта в початковій точці, тобто:

; .

Врахуємо також, що управління за координатами здійснюється протилежно градієнту, тобто:

; .

Швидкість відпрацювання виконавчих пристроїв:

; .

З останніх рівнянь знаходимо:

х₁ = - 2К₂К₃х₁₀τ + С₁; х₂ = - 2К₂К₄х₂₀τ + С₂ .

З початкових умов (при τ = 0) знаходимо: С₁ = х₁₀; С₂ = х₂₀ і кінцево маємо:

х₁ = - 2К₂К₃х₁₀τ + х₁₀ ; х₂ = - 2К₂К₄х₂₀τ + х₂₀ .

Підставимо вирази для х₁ та х₂ в рівняння об’єкту:

=

.

Позначимо:

= ; = ; = .

і отримуємо неоднорідне рівняння:

.

Вирішуємо його методом невизначених множників. Рішення однорідного рівняння має вигляд:

; .

Підставимо знайдені вирази для у та в неоднорідне рівняння:

; .

Невизначений множник А(τ) знаходимо інтегруванням А^/(τ):

.

Інтеграли в цій формулі є табличними:

; ; .

Тоді маємо:

;

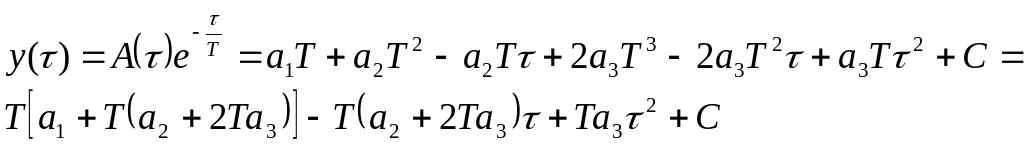
З початкових умов знаходимо сталу інтегрування і рішення рівняння:

;

;

,

або після підстановки числових даних:

а₂ = 0,0064; а₃ = 0,00004096; у(τ) = 4 – 0,160768τ + 0,0008192τ²

При часі пошуку τ = 20; 25; 26с значення вихідного параметра становить відповідно у(20) = 1,11232; у(25) = 0,4928; у(26) = 0,373, тобто тривалість пошуку за методом найшвидшого спуску складає біля 25,7с, що майже в 4 рази менш, ніж при застосуванні методу градієнтів.

Окрім розглянутих, застосовують також метод спряжених напрямків і, як його модифікація, розроблений Р. Флетчером та Ц. М. Рівсом метод спряженого градієнта.

Метод Ньютона відноситься до групи методів другого порядку. В ньому використовуються перші та другі похідні цільової функції; необхідні умови безумовного екстремуму F(X) = 0 розглядаються як система алгебраїчних рівнянь, яка вирішується за методом Ньютона. Достоїнством методу є висока збіжність, яка є вищою, ніж у методів нульового та першого порядку. Але метод потребує складних розрахунків і при великий відстані початкової точки від оптимуму взагалі можна не досягнути його. Тому цей метод доцільно використовувати на заключному етапі пошуку. Для скорочення обчислювальних процедур використовують також модифіковані методи Ньютона, методи змінної метрики.