Вихідні дані до задачі про склад сировини

Характеристика	Матеріал
	Метал	Скло	Пластмаса
Вартість, грн/м2	25	20	40
Маса, кг/м2	10	15	3

Рішення. Позначимо х₁, х₂, х₃ – кількість металу, скла та пластмаси, м². Задача формалізується наступним чином:

min F=25x₁+20x₂+40x₃

при обмеженнях:

10х₁+15х₂+3х₃ 150; (1)

х₁+х₂+х₃=14; (2)

х₁ 0; (3)

4 х₂ 5; (4)

х₃ 0. (5)

З рівняння (2) маємо:

х₁ = 14 - х₂ - х₃.

З нерівності (1) з урахуванням отриманого значення х₁ визначаємо х₃ :

х₁ 15 - 1,5х₂ - 0,3х₃; 14 - х₂ - х₃ 15 - 1,5х₂ - 0,3х₃; х₃ .

З (2) та (3) отримуємо:

х₁ = 14 - х₂ - х₃ 0; х₃ 14 - х₂ .

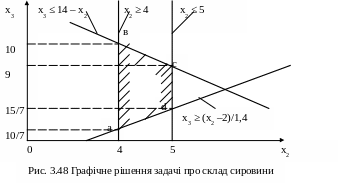
Множина припустимих рішень задачі показана на рис. 3.48.

Координати вершин багатокутника та значення цільової функції в них:

-а: х₂ = 4; х₃ = ; х₁ = 14 –4 - ; F=25* ;

-в: х₂ = 4; х₃ = 14 – 4 = 10; х₁ = 14 – 4 – 10 = 0; F=25*0+20*4+40*10=480;

-c: х₂ = 5; х₃ = 14 – 5 = 9; х₁ = 14 – 5 – 9 = 0; F = 25*0 + 20*5 + 40*9 = 460;

-d: x₂ = 5; х₃ = ; х₁ = 14 – 5 - ;

F = 25 + 20*5 + 40 = 357,14.

Тобто, найкращою є точка а з координатами:

х₁^* = ; х₂^* = 4; х₃^* = .

Третьою класичною задачею лінійного програмування є задача планування виробництва, де розглядається деяке підприємство, яке випускає n типів виробів і витрачає на них m типів ресурсів. Позначимо:

• а_ij – кількість і – того ресурсу для виробництва одиниці j – того виробу; а_ij ≥ 0; і = 1, 2,…,m; j = 1, 2,…, n;

• в_і – запас і – того ресурсу на підприємстві; в_і > 0;

• с_j – ціна одиниці j – того виробу; с_j > 0;

• х_j – об’єм виробництва j – того виробу, що планується.

Припускається, що технологія виробництва є лінійною, тобто витрати ресурсів зростають прямо пропорційно об’єму виробництва. Окрім того, немає обмежень щодо збуту виробів на ринку, тобто будь – який набір виробів даного підприємства користується попитом.

Припустимим є такий набір виробів, при якому сумарні витрати кожного і – того ресурсу не перевищують його запасу:

(1)

Окрім того, існує природно обмеження:

х_j ≥ 0. (2)

Вартість набору виробів становить:

. (3)

Задача формулюється наступним чином: серед всіх наборів виробів, які випускаються та задовольняють обмеженням (1) і (2), треба знайти такий, при якому величина (3) приймає найбільше значення.

Приклад. Підприємство випускає два види продукції А₁ та А₂ і використовує при виробництві кожного з них три види сировини В₁, В₂, В₃. Норми витрати сировини, об’єми її запасів і прибуток від реалізації 1 тони продукції кожного виду наведені в табл. 3.5. Треба скласти план виробництва продукції А₁ і А₂, який забезпечує максимум сумарного прибутку.

Таблиця 3.5

Вихідні дані до задачі планування виробництва

Сировина	Норми витрат, т/т		Об’єм запасів, т
	А1	А2
В1	0,5	0,2	600
В2	0,2	0,6	870
В3	0,3	0,2	430
Прибуток від реалізації 1 т продукції, грн.	320	290

Рішення. Позначимо об’єми виробництва продукції А₁ та А₂ через х₁ та х₂. Тоді задача формалізується наступним чином:

max F = 320х₁ + 290х₂

при обмеженнях:

0,5х₁ + 0,2х₂ ≤ 600;

0,2х₁ + 0,6х₂ ≤ 870;

0,3х₁ + 0,2х₂ ≤ 430;

х₁ ≥ 0; х₂ ≥ 0.

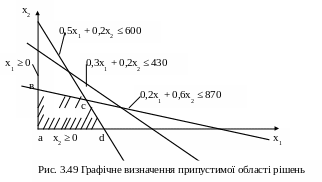
На рис. 3.49 побудована припустима область рішень за допомогою означеної системи обмежень. Координати вершин багатокутника та значення цільової функції в них:

- точка а: х₁ =0; х₂ = 0; F = 0;

- точка в: х₁ =0. Точка в знаходиться на перетині ліній х₁ ≥ 0 та 0,2х₁ + 0,6х₂ ≤ 870, тому координату х₂ визначаємо з рівності:

0,2*0 + 0,6*х₂ = 870; х₂ = 1450; F = 320*0 + 290*1450 = 420500;

- точка с. Координати визначаємо з сумісного рішення рівнянь:

0,5х₁ + 0,2х₂ = 600; 0,2х₁ + 0,6х₂ = 870.

З першого рівняння визначаємо х₁ через х₂:

х₁= 1200 – 0,4х₂ .

Тоді з другого рівняння знаходимо х₂:

0,2(1200 – 0,4х₂) + 0,6х₂ = 870; х₂ = 1211,54.

Значення координати х₁ та цільової функції:

х₁ = 1200 – 0,4*1211,54 = 715,38; F = 320*715,38 + 290*1211,54 = 580270;

- точка d: х₂ = 0. З рівняння 0,5х₁ + 0,2х₂ = 600 отримуємо:

х₁ = 1200 і цільова функція F = 320*1200 + 290*0 = 384000.

Таким чином, рішенням є точка с з координатами:

х₁^* = 715,38; х₂^* = 1211,54.

Для рішення задач умовної оптимізації використовують методи нелінійного програмування з обмеженнями. Задачу умовної оптимізації можна вирішити за допомогою двох підходів:

1) звести цю задачу до задачі безумовної оптимізації, враховуючи ту обставину, що найбільш розвинутими є методи пошуку безумовного екстремуму;

2) застосувати спеціальні методи для задач нелінійного програмування з обмеженнями.

Зведення задачі умовної оптимізації до безумовної виконується з урахуванням прямих та функціональних обмежень. Усунення прямих обмежень здійснюється нормуванням керованих параметрів. Наприклад, при прямому обмеженні а < u_i < в нормування виконують за формулою:

.

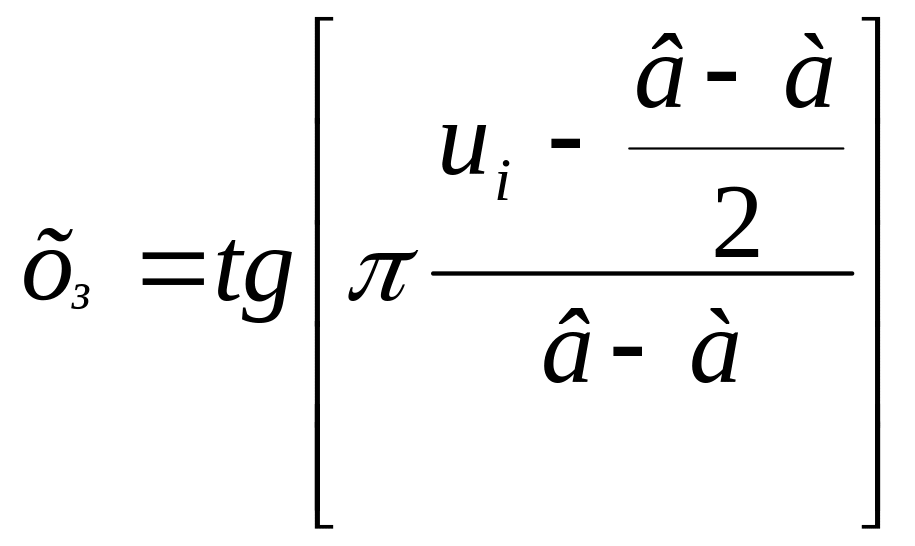Це дозволяє перетворити обмежений параметр u_i в необмежений х_і.

Функціональні обмеження усувають шляхом конструювання узагальненої функції оптимізації з урахуванням типу обмежень. Так, при обмеженні типу ψ(Х) = 0 перехід до безумовної оптимізації здійснюється за методом невизначених множників Лагранжа. Нова цільова функція – функція Лагранжа Ф(Х, Λ) – формується з вихідної цільової функції F(Х) і всіх функціональних обмежень типу рівностей наступним чином:

,

де Λ = (λ₁, λ₂,…., λ_m) – вектор невизначених множників Лагранжа;

ψ_j (X) = 0 – j – те обмеження типу рівності;

m – кількість обмежень.

Для отримання значень n невідомих керованих параметрів х₁, х₂,…, х_n і m множників Лагранжа λ₁, λ₂,…., λ_m вирішують систему алгебраїчних рівнянь, яка відображує необхідні умови екстремуму функції Лагранжа:

при і = 1, 2,…,n;

при j = 1, 2,…., m.

Система вирішується єдиним чином, якщо виконується умова:

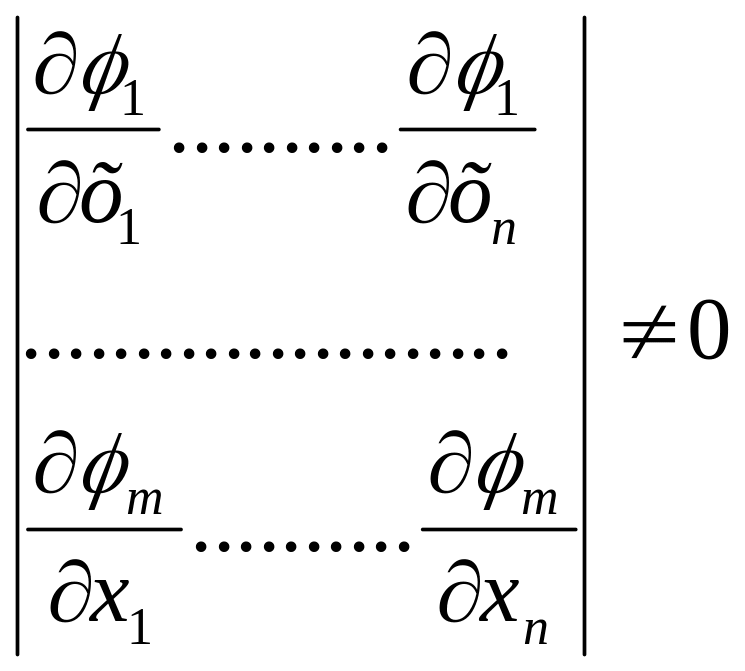
Функція Лагранжа і цільова функція в припустимій області співпадають. Тому, якщо знайдено оптимальне значення функції Лагранжа, то воно буде водночас і умовним оптимумом цільової функції F(X).

Для рішення задач оптимізації з обмеженнями використовують методи штрафних функцій. В їх основі лежить перетворення умовної задачі в одну або послідовність декількох задач без обмежень. Перевагою цих методів є здійснення пошуку більш простими методами безумовної оптимізації. Найбільш розповсюдженими з них є методи внутрішньої та зовнішньої точки.

В

minF(X)

XЄХП

методах внутрішньої точки траєкторію пошуку утримують усередині припустимої області за допомогою так званої бар’єрної функції. Якщо

поставлена задача при обмеженнях φ_j(X) ≥ 0, j = 1, 2,…., m, то в

якості бар’єрної функції можна вибрати, наприклад, функцію:

.

Тоді задача перетворюється в еквівалентну послідовність задач безумовної оптимізації, тобто:

min Ф(X, r_k) = min [F(X) + Θ(X, r_k)]

X Є ХП Х Є ХП

де к – номер задачі.

Значення r_k є позитивним і наближується до 0 при наближенні к до безкінечності.

Сутність методу внутрішньої точки полягає у наступному.

Вибирають вихідну точку всередині припустимої області. При фіксованому r_к виконують мінімізацію функції Ф(Х, r_k) одним з методів безумовної оптимізації. Якщо в процесі пошуку точка траєкторії наближується до границі області, відповідний елемент φ_j(Х) вектору обмежень стає близьким до нуля і бар’єрна функція необмежено зростає. Потім r_k зменшують і повторюють пошук при r₂ < r₁ . Значення параметру r₁ на першому кроці звичайно приймають 1.

В методах зовнішньої точки узагальнююча функція для безумовної оптимізації також будується шляхом об^/єднання вихідної цільової функції і функції штрафу, але у якості функції штрафу вибирають інші вирази, наприклад:

,

де r_k > 0; r_k → ∞ при к → ∞ .

Узагальнююча функція має вигляд:

Ф(Х, r_k) = F(X) + Θ(X, r_k)

Значення функції штрафу залежить від значення r_k . Зі зростанням r_k умовний мінімум F(X) та безумовний мінімум Ф(Х, r_k) зближуються і при r_k → ∞ вони співпадають.

Для рішення задач умовної оптимізації з обмеженнями використовують також метод проекції градієнта та його модифікації – проективні методи або градієнтні методи з великою довжиною кроку.

Для рішення задач з урахуванням ситуаційних змін використовують метод динамічного програмування. Він був розроблений групою американських математиків на чолі з Р. Белманом.

В основу методу покладено принцип оптимальності, який являє собою одну з основних властивостей оптимального детермінованого процесу: слід шукати завжди оптимальне продовження процесу відносно того стану, якого досягнуто в даний момент. Тобто оптимальне управління процесом в будь – який момент часу не залежить від його попередньої історії, а визначається лише заданою ціллю та станом системи в даний момент часу.

Припустимо, що об’єкт описує система диференційних рівнянь:

,

або у векторному вигляді: ,

де і = 1, 2, …, n – координата об’єкта;

n – кількість координат (розмірність системи);

m – кількість управляючих дій на об’єкт;

Х – n – вимірний вектор фазового простору;

U – m – вимірна управляюча функція.

Задачею динамічного програмування є знаходження такого припустимого управління U(τ), 0 ≤ τ ≤ Т, при якому забезпечується мінімізація (або максимізація) цільової функції:

,

де Т – фіксована тривалість руху.

Функцією F може бути кількість отриманої продукції, витрата енергії, ресурсів і т. д.

Принцип оптимальності полягає у наступному.

Починаючи з будь – якого моменту часу τ^/; 0 ≤ τ^/ ≤ Т ділянка оптимальної траєкторії від Х(τ^/) до Х(Т) сама по собі також є оптимальною траєкторією. Інший смисловий аспект принципу оптимальності: якщо в деякий момент часу управління було неоптимальним, то наслідки цього відхилення від оптимального управління вже неможливо виправити в майбутньому.

Для покрокової процедури динамічного програмування:

,

де N – загальна кількість інтервалів (кроків);

u₁(k), u₂(k),…; х₁(к), х₂(к), … - управляючі дії і координати на к – тому кроці.

Оптимальний процес буде відомий тоді, коли будуть знайдені значення управлінь u₁^*, u₂^*,…., u_m^* на всіх к = 1, 2, …, N кроках (циклах), які мінімізують (або максимізують) цю суму (або інтеграл). Слід відзначити, що в методі динамічного програмування функція мінімізується (або максимізується) у зворотному порядку – з кінця до початку процесу.

Приклад. Деяка початкова сума коштів S = х(1) витрачається на придбання обладнання двох типів А та В для організації виробництва. Якщо на обладнання А виділити суму u(1), 0 ≤ u(1) ≤ х(1), то за певний період його експлуатації буде отриманий прибуток g(u(1)). При цьому решта коштів (х(1) – u(1)) витрачається на обладнання В, яке за той же строк роботи дає прибуток h(x(1) – u(1)).

Таким чином, до кінця строку експлуатації загальний прибуток складе:

R₁(x(1), u(1)) = g(u(1) + h(x(1) – u(1)).

Потім амортизоване обладнання реалізують, від продажу обладнання А отримують суму аu(1), 0 < a < 1, а від продажу обладнання В – в(х(1) – u(1)), 0 < в < 1. Загальна сума отриманих коштів:

х(2) = аu(1) + в(х(1) – u(1)).

Їх використовують як початкову суму для другого циклу. Якщо з цієї суми на нове обладнання А виділити u(2) коштів, а на обладнання В – (х(2) – u(2)), 0 ≤ u(2) ≤ х(2), то за той же час експлуатації в другому циклі буде отриманий прибуток g(u(2) + h(x(2) – u(2)) і підсумковий прибуток за два цикли складатиме:

R₂(x(1), u(1), u(2)) = g(u(1) + h(x(1) – u(1)) + g(u(2) + h(x(2) – u(2)) .

В кінці другого циклу обладнання, яке відпрацювало свій строк, знову реалізують, а отриману від його продажу суму х(3) = аu(2) + в(х(2) – u(2)) використовують як початкову для третього циклу і т. д.

Вважаючи функції прибутку g(ν), h(μ) від експлуатації обладнання А і В, а також константи S, a, в заданими і однаковими в кожному циклі, треба знайти таку стратегію розподілу коштів для купівлі обладнання А і В у кожному циклі, щоб забезпечити найбільший прибуток після фіксованого числа n виробничих циклів. Тобто треба так вибрати значення u(1), u(2), …,u(n) в припустимих межах, щоб максимізувати величину:

R_n(x(1), u(1), u(2),….,u(n)) = [g(u(m)) + h(x(m) – u(m))] (1),

де х(1) = S;

х(к + 1) = аu(k) + в(х(к) – u(к), к = 1, 2, …, n;

0 ≤ u(m) ≤ x(m), m = 1, 2,…., n

Для переходу від (к – 1) – того циклу до к – того необхідно знати лише величину х(к) і число (n – к) циклів, які залишилися; ніяка інформація щодо “історії” процесу не має значення, оскільки вона не впливає на майбутнє.

Для рішення задачі використовують прийом зворотного руху від кінця до початку процесу розподілу коштів, що здійснюється у багато етапів. Розглядають лише останній цикл, знаходять значення управління, яке є оптимальним в цьому циклі, як функцію стану процесу на початку останнього циклу. Потім переходять до розгляду двох останніх циклів. Знаходять значення управління, яке є оптимальним на передостанньому циклі, як функцію стану процесу на початку цього циклу. В результаті такого вибору в кінці цього циклу процес набуває стану, який є початковим для останнього циклу. За цім станом, використовуючи вже отримані результати для останнього циклу, визначають оптимальне значення управління на останньому циклі і т. д. В кінцевому рахунку приходять до початку процесу і використовують заданий початковий стан.

В нашому прикладі увесь виробничий процес, який включає n циклів, розглядаємо як такий, що має багато етапів. Припустимо, що пройшло вже (n - 1) послідовних циклів і до початку n – го циклу маємо вихідну суму х(n). При фіксованій величині х(n) в залежності від вибору u(n), 0 ≤ u(n) ≤ x(n) в кінці n – ного циклу отримуємо прибуток g(u(n)) + h(x(n) – u(n)).

Оптимізація в n – ному циклі не залежить від того, як проходили попередні цикли, і полягає в отриманні максимального прибутку:

r_n(x(n)) = max[g(u(n)) + h(x(n) – u(n))]

0 ≤ u(n) ≤ x(n)

при припустимому значенні u^*(n), яке відповідає досягненню цього максимального прибутку. Очевидно, що як величина r_n(x(n)) , так і значення u^*(n) залежать лише від вихідної суми х(n).

Зсунемося на один цикл до початку процесу і розглянемо задачу максимізації сумарного прибутку за два останніх цикли при фіксованій вихідній сумі х(n - 1), тобто задачу пошуку:

r_{n -1}(x(n - 1)) = max[g(u(n - 1)) + h(x(n - 1) – u(n - 1)) + g(u(n)) + h(x(n) – u(n))] ;

0 ≤ u(n - 1) ≤ x(n – 1); 0 ≤ u(n) ≤ x(n).

Оскільки g(u(n - 1)) та h(x(n - 1) – u(n - 1)) не залежать від u(n), то:

r_{n -1}(x(n - 1)) = max[g(u(n - 1)) + h(x(n - 1) – u(n - 1)) + r_n(au(n - 1) + в(x(n - 1) – u(n - 1))] ;

0 ≤ u(n - 1) ≤ x(n – 1).

Тобто, ми визначили r_n (x(n)) і величину х(n) через х(n - 1) та u(n –1). Припустиме значення u^*(n –1), при якому досягається максимальний сумарний прибуток r_{n -1}(x(n - 1)) залежить від величини х(n - 1).

Якщо продовжити зворотній рух до початку процесу, то отримуємо, що сумарний максимальний прибуток за (n - к) останніх циклів дорівнює:

r_{n -к}(x(n - к)) = max[g(u(n - к)) + h(x(n - к) – u(n - к)) + r_{n +1 - к}(au(n - к) + в(x(n - к) – u(n - к))] ;

0 ≤ u(n - к) ≤ x(n – к);

к = 1, 2, …, n – 1

Це рекурентне співвідношення Белмана для даної задачі. Воно зводить оптимізацію в (n - к) останніх циклах до оптимізації в (n – к) – тому циклі. Оскільки з визначення величини r₁(x(1)) і цільової функції випливає рівність:

r₁(x(1)) = maxR_n(x(1), u(1), u(2),…, u(n));

0 ≤ u(m) ≤ x(m); m = 1, 2, …, n ,

то за допомогою рекурентного співвідношення задача пошуку максимуму цільової функції n змінних перетворюється в послідовність n задач знаходження максимуму функції однієї змінної. Тобто, це співвідношення дає зручний для обчислення алгоритм рішення вихідної задачі.

В системному аналізі широко застосовують методи дослідження операцій. Термін “дослідження операцій” виник за назвою підрозділу британської армії, який на початку другої світової війни займався застосуванням обчислювальних методів для обробки результатів радарних спостережень. Саме тому в мові теорії дослідження операцій досить широко використовуються деякі військові терміни: операція, стратегія і т. д.

Операцією називають сукупність дій, скерованих на досягнення певної мети. Операційною стороною називають сукупність осіб, які прагнуть до цієї мети. Крім того, в операційній ситуації можуть бути присутні й інші особи, які впливають на хід операції та мають власні цілі. Їх поряд з іншими чинниками, що впливають на операцію, але не підпорядковуються операційній стороні (наприклад, природні фактори), відносять до неконтрольованих факторів (чинників) операції. Операційна сторона може мати дослідника операції, тобто аналітика, який складає та досліджує математичну модель операції, але не приймає остаточного рішення. Ресурси для досягнення мети називають активними засобами. Неконтрольовані чинники залежно від інформованості про них дослідника поділяються на:

1. фіксовані, тобто чинники, значення яких точно відомі;

2. випадкові, тобто випадкові величини з відомими розподілами;

3. невизначені, тобто детерміновані або випадкові величини, щодо яких відома лише область можливих значень або клас можливих законів розподілу.

Комплекс можливих дій для досягнення мети із застосуванням активних засобів, що може здійснювати операційна сторона, називається стратегією. Головна задача дослідження операцій – це порівняння різних стратегій та вибір найкращої в певному розумінні серед них.

Якщо неконтрольовані чинники є фіксованими, то пошук оптимальної стратегії – це задача теорії звичайної оптимізації. Основне місце серед методів рішення таких задач займають методи математичного програмування. Це викликано тим, що ці задачі є звичайно некласичними екстремальними, до них, за невеликим виключенням, неможливо застосувати класичні методи диференційного числення. Якщо всі функції в опису критерію ефективності і обмежень є лінійними, то це задача лінійного програмування. Якщо розв’язки задач за своїм змістом повинні бути цілими числами, то це задача цілочислового програмування. В разі нелінійних функцій, які описують критерій і простір стратегій, застосовують методи нелінійного програмування. Якщо критерій заданий через функцію, яка описує процес розвитку операцій в часі, то це задача динамічного програмування. Коли критерій та простір стратегій описуються опуклими структурами, то задача належить до опуклого програмування.

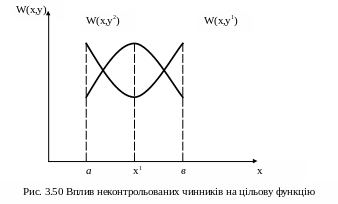
Значно складнішою є справа, коли неконтрольовані чинники є нефіксованими. Тоді може статися, що стратегія х¹, яка є оптимальною при значеннях неконтрольованих чинників у¹, може бути поганою і навіть найгіршою при інших значеннях неконтрольованих чинників (рис. 3.50).

Тому в даному випадку застосовують оцінки ефективності стратегій гарантовані та середні .

Гарантовану оцінку застосовують, коли розраховують на найгіршу поведінку неконтрольованих факторів:

,

якщо критерій W заданий в позитивному інгредієнті, та:

,

якщо він заданий в негативному інгредієнті.

Тут У – опис множини можливих значень, тобто, простору неконтрольованих факторів.

Шляхом максимізації (мінімізації) при всіх х Є Х отримуємо оптимальну гарантовану стратегію х_*¹, яка забезпечує найкращий гарантований результат операції :

;

,

де Х – опис множини можливих стратегій, тобто, простору стратегій.

Середню оцінку ефективності визначають шляхом усереднення значень критерію ефективності W(х, у) при всіх у Є У. Якщо простір У кінцевий або зліченний, то середня оцінка:

,

де а_і – коефіцієнт ваги фактору у_і при усередненні; а_і ≥ 0; ;

І – підмножина, яку пробігають неконтрольовані фактори, з множини натуральних чисел.

Стратегія, яка задовольняє умові або , називається оптимальною у середньому.

При наявності випадкових та невизначених неконтрольованих факторів, що не є фіксованими, вирішуються мінімаксні задачі з гарантованими оцінками ефективності, задачі прикладної теорії імовірностей, теорії випадкових процесів, прикладної статистики. До них традиційно відносять задачі теорії масового обслуговування, теорії черг, теорії управління запасами, теорії надійності, стохастичного управління, статистичного моделювання, теорії статистичних розв’язків, статистичного контролю якості, статистичної теорії прогнозування, теорії планування експерименту тощо.

Одним з розділів теорії дослідження операцій є теорія ігор. Це математична теорія прийняття рішень в умовах конфліктів. Конфлікт полягає в тому, що інтереси сторін не співпадають або сторони переслідують протилежні цілі. Гра або боротьба може вестися проти організованого супротивника (військові операції, спортивні ігри) або проти сил природи (випадкового процесу). Сторона вибирає таку стратегію, яка забезпечує їй найбільший виграш, який і є метою гри. Зазначимо тут, що стратегія – це сукупність правил поведінки кожної сторони на дії іншої.

Зародження теорії ігор як математичної дисципліни пов’язують з листом Б. Паскаля до П. Ферма від 29 червня 1654 р., в якому розглядалися математичні моделі деяких азартних ігор, і яке також вважають початком математичної теорії імовірностей. Основні ідеї сучасної теорії ігор викладені Дж. фон Нейманом 1928р. Ці ідеї були розвинуті ним разом з американським економістом О. Моргенштерном у монографії “Теорія ігор та економічна поведінка” 1943 р. Вважаючи, що ринкова економіка – це насамперед економіка конфліктів, Дж. фон Нейман вбачав саме в математичній теорії конфліктів адекватний апарат для опису та дослідження економічних явищ. Після цього почався інтенсивний розвиток теорії ігор як спеціального розділу математики. Ця теорія є однією з найважливіших складових частин сучасної кібернетики, дослідження операцій та математичної економіки.

В теорії ігор невизначеність пов’язана з діями інших учасників операції, які мають свої цілі, а також з іншими обставинами операції, її природою. Учасники гри можуть утворювати коаліції дій, тобто діяти разом, і коаліції інтересів, тобто мати певні спільні інтереси. В останньому випадку мають місце так звані коаліційні ігри, серед яких найбільш розповсюджені кооперативні ігри, коли має місце одна коаліція дій та декілька коаліцій інтересів. Якщо коаліцію утворити неможливо, то ігри є безкоаліційними. В них гравці послідовно приймають рішення за умов неповної та змінної з часом інформації, наприклад, це гра в шахи, шашки. Подібний клас називають класом позиційних ігор і теоретичним апаратом них є послідовний статистичний аналіз.

Безкоаліційна гра називається грою зі сталою сумою, якщо виконується умова:

для всіх ситуацій s Є S,

де С – деяка стала;

S – сім^/я множин стратегій;

H_i – сім^/я множин виграшу; і Є І

В разі С = 0 гра називається грою з нульовою сумою. Така гра з нульовою

сумою, коли дві сторони мають протилежні інтереси, називається антагоністичною. В такий парній грі вибір стратегії виконується за принципом “обережності”, коли одна сторона отримує найкращий результат при найгірших по відношенню до неї діях іншої сторони. Скінченні антагоністичні ігри ще називають матричними, тому що функція виграшу позначається матрицею:

H = (а_ij); і Є S₁; j Є S₂,

де S₁ та S₂ – сукупність можливих стратегій першого та другого гравця.

Матрицю Н називають платіжною. В ній кожен елемент а_ij є виграшем першого гравця, якщо він обрав стратегію і Є S₁, а другий гравець обрав стратегію j Є S₂. Відповідно величина ( - а_ij) буде виграшем другого гравця за такої ж самої ситуації.

Якщо позначити стратегії номерами S₁ = {1, 2,…, n} та S₂ = {1, 2,…, m}, то числа:

;

вказують на мінімальний можливий виграш першого гравця при виборі стратегії і та на максимально можливий виграш другого гравця при виборі стратегії j відповідно. Величина називається нижньою ціною гри, а стратегія і₀ , така що забезпечує α = α_і0, тобто нижню ціну гри, - максимінною стратегією. Це оптимально гарантована стратегія першого гравця, тому що при будь – якому виборі другого гравця йому буде забезпечений виграш не менший, ніж α.

Величина називається верхньою ціною гри (мінімаксом гри), а стратегія j₀ другого гравця, така що забезпечує β = β_j0 – мінімаксною стратегією. Стратегія j₀ є оптимально гарантована стратегія другого гравця, бо, обираючи її, він програє не більше, ніж β = β_j0 .

В матриці може існувати сідлова точка (і₀, j₀), в який елемент а_і0,j0 водночас є максимальним в своєму стовпчику і мінімальним в своєму рядку. В сідловій точці ціна гри а_і0,j0 = α = β і для обох гравців оптимальним є вибір максимінної або мінімаксної стратегій і₀ та j₀. Відхилення одного з гравців від оптимальної стратегії невигідне для нього, якщо інший гравець діє розумно.

Приклад. Припустимо, що в грі зі стратегіями S₁ = {1, 2, 3}; S₂ = {1, 2, 3, 4} платіжна матриця має вигляд:

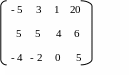
Ця матриця має сідлову точку (2, 3), тому що 4 є водночас мінімумом другого рядка та максимумом третього стовпчика. Тобто, для першого гравця оптимальною є стратегія 2, а для другого – стратегія 3, причому ціна гри дорівнює 4.

Подібні стратегії гравців називають чистими. Якщо платіжна матриця не має сідлової точки, наприклад:

, ,,

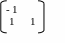
то використовують так звані змішані стратегії. В них кожен з гравців обирає стратегії і Є S₁ = {1, 2,…, n}; j Є S₂ = {1, 2,…, m} згідно з деякими імовірнісними розподілами:

Р = {p₁, p₂,…,p_n}; Q = {q₁, q₂,…, q_m}.

Тобто, перший гравець обирає стратегію і Є S₁ з імовірністю p_і, а другий приймає стратегію j Є S₂ з імовірністю q_j, причому кожен з них діє незалежно один від одного. Для імовірнісних розподілів Р та Q діють звичайні умови:

0 ≤ Р_і ≤ 1; 0 ≤ q_j ≤ 1; .

Математичне сподівання виграшу першого гравця і, відповідно, програшу другого, оскільки вони діють незалежно, визначається виразом:

Е(Р, Q) = .

За теоремою Дж. фон Неймана існують оптимальні змішані стратегії гравців, які забезпечують сідлову точку функції математичного сподівання виграшу, де ціна гри складає ν (максимінна для першого гравця і мінімаксна – для другого).

Задача визначення оптимальних змішаних стратегій гравців може бути зведена до пари двоїстих задач лінійного програмування. В цьому випадку задача першого гравця має вигляд:

f₁ = ν → max;

;

Задача другого гравця:

f₂ = ν → min;

;

.

Інколи для спрощення рішення цих задач переходять до нових змінних:

х_і = ; у_j =

і задача отримує вигляд:

F₁ = ; х_і ≥ 0; і = 1, 2,…, n;

F₂ = ; y_j ≥ 0; j = 1, 2,…, m.

Приклад використання теорії матричних ігор. Підприємець може налагодити виробництво продукції А₁, А₂ або А₃. На збут продукції впливає стан споживчого ринку. Треба встановити, який товар треба випускати, щоб забезпечити максимальний прибуток, якщо відомі ціни а_і за одиницю товару А_і і її середній об’єм збуту в залежності від стану споживчого ринку, тобто при падінні попиту, нормальному попиті та зростанні попиту, причому надійного прогнозу щодо майбутнього попиту немає.

Рішення. За умовами задачі у підприємця є три стратегії: випускати товар А₁, А₂ або А₃. Другим “гравцем” тут є стан споживчого ринку, який також має три стратегії: падіння попиту, стабільний попит, зростання попиту. Якщо виграшем вважати прибуток підприємця, то платіжна матриця його гри має вигляд:

В цій матриці в_іj – попит на і – тий товар при j – тому стані ринку.

Ще один приклад. Два гравці мають стратегії S₁ = (1, 2); S₂ – (1, 2, 3). Платіжна матриця гри не має максимінної точки:

Рішення. Позначимо Р = (х, 1 – х), 0 ≤ х ≤ 1 змішану стратегію першого гравця. Тобто він приймає стратегію і = 1 з імовірністю х, а стратегію і = 2 з імовірністю (1 – х). Якщо другий гравець застосує чисту стратегію j = 1, то очікуваний платіж першого гравця буде:

у₁ = Е(Р, j = 1) = 2x + 7(1 – x) = 7 – 5x.

Якщо другий гравець застосує чисті стратегії j = 2 або j = 3, то платіж першого гравця буде відповідно:

у₂ = Е(Р, j = 2) = 3x + 5(1 – x) = 5 – 2x;

у₃ = Е(Р, j = 3) = 11x + 2(1 – x) = 2 + 9x.

Побудуємо ці прямі на рис. 3.51.

При виборі першим гравцем стратегії Р = (х, 1 – х) він може бути впевненим, що одержить виграш не менше, ніж під нижньою обвідною ломаної лінії авсd. Найвища точка цієї лінії в відповідає значенню х_*, при якому виграш у має максимум. В цій точці у₂ = у₃; 5 – 2х = 2 + 9х, звідки знаходимо: х_* = . Тоді оптимальна стратегія першого гравця Р_* = ( ), а ціна гри:

у_* = 2 + 9х_* = 2 + 9* = .

Теорія диференційних ігор використовується для вивчення управління об’єктами, рух яких описується диференційними рівняннями, в конфліктних ситуаціях, тобто коли цілі об’єктів не співпадають. Це задачі оптимального переслідування одного керованого об’єкта іншим (літака зенітною ракетою, літака літаком) або, навпаки, ухилення від зустрічі об’єктів; задача приведення керованого об’єкта в деякий заданий стан при дії заздалегідь невідомих збурень (задача наведення); задача керування об’єктом при неповній поточній інформації щодо його стану та аналогічні задачі.