Пример выполнения задания 1

Дан ряд распределения случайной величины.

X	-3	-1	2	4	5
P	0,2	0,3	0,2	0,1	0,2

> restart;with(stats):with(describe):with(plots):

Вводим значения случайной величины:

> X:=[-3,-1,2,4,5];n:=count(X);

_{X:=[-3,-1,2,4,5]}

_n:=5

Вводим соответствующие вероятности:

> P:=[0.2,0.3,0.2,0.1,0.2];

_{P:=[0.2,0.3,0.2,0.1,0.2]}

Проверка корректности задания случайной величины:

> sum('P[i]','i'=1..n);

_1.0

Строим многоугольник распределения:

>a:=pointplot([[X[1],P[1]],[X[2],P[2]],[X[3],P[3]],[X[4],P[4]],[X[5],P[5]]]):

>b:=plot([[X[1],P[1]],[X[2],P[2]],[X[3],P[3]],[X[4],P[4]],[X[5],P[5]]]):

> display([a,b]);

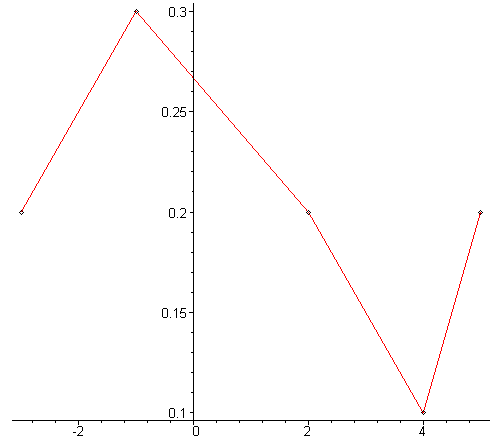
Запишем функцию распределения случайной величины X и построим её график.

> F:=piecewise(x<=X[1],0,x>X[1]and x<=X[2],P[1],x>X[2]and x<=X[3],P[1]+P[2],x>X[3]and x<=X[4],P[1]+P[2]+P[3],x>X[4]and x<=X[5], P[1]+P[2]+P[3]+P[4],x>X[5],P[1]+P[2]+P[3]+P[4]+P[5]);

> plot(F,x=X[1]-5..X[n]+5);

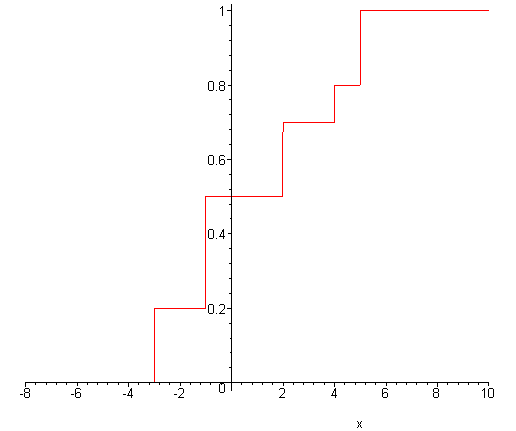
Найдём математическое ожидание случайной величины X:

> MO:=sum('X[i]*P[i]','i'=1..n);

_MO:=0.9

Найдём дисперсию X:

> Dis:=sum('(X[i])^2*P[i]','i'=1..n)-M^2;

_Dis:=8.69

Задание 2. Задана плотность распределения непрерывной случайной величины . Требуется:

а) найти параметр ;

б) найти функцию распределения случайной величины ;

в) построить графики функции и плотности распределения случайной величины ;

г) найти математическое ожидание и дисперсию случайной величины ;

д) найти вероятность того, что случайная величина примет значение в интервале .

Варианты заданий

Вариант 1. , .

Вариант 2. , .

Вариант 3. , .

Вариант 4. , .

Вариант 5. , .

Вариант 6. , .

Вариант 7. , .

Вариант 8. , .

Вариант 9. , .

Вариант 10. ,

Вариант 11. , .

Вариант 12. , .

Вариант 13. , .

Вариант 14. , .

Вариант 15. , .

Вариант 16. , .

Вариант 17. , .

Вариант 18. , .

Вариант 19. , .

Вариант 20. , .

Вариант 21. , .

Вариант 22. , .

Вариант 23. , .

Вариант 24. , .

Вариант 25. , .

Вариант 26. , .

Вариант 27. , .

Вариант 28. , .

Вариант 29. , .

Вариант 30. , .

Пример выполнения задания 2

Задана плотность распределения непрерывной случайной величины .

, .

> restart:

Вводим плотность распределения случайной величины :

> p:=x->piecewise(x>=1 and x<=3,c*(x-1)^2,x<1 and x>3,0);

p:=x→piecewise(1≤x and x≤3,c(x-1)²,x<1 and x>3,0)

а) Найдём параметр из уравнения :

>c:=solve(int(p(x),x=-infinity..infinity)=1,c);

c:=3/8

б) Функцию распределения находим по формуле :

>F:=int(p(x),x);

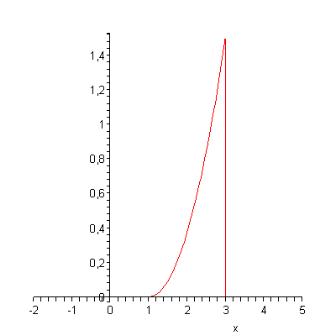
в) Строим графики плотности и функции распределения случайной величины:

>plot(p(x),x=-2..5);

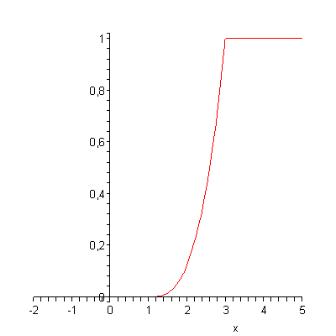
>plot(F,x=-2..5).

г) Найдём математическое ожидание и дисперсию случайной величины по формулам , :

> MO:=int(x*p(x),x=-infinity..infinity);

>DIS:=int(x^2*p(x),x=-infinity..infinity)-MO^2;

д) Найдём вероятность того, что случайная величина примет значение в интервале по формуле .

>P(2<xi and xi<5):=int(p(x),x=2..5);