Вариант №18
I. 
.
II.а. 
.
II.б. 
.
III. Даны
точки:
.
Вычислить:
а. Косинус угла между векторами и .
б. Площадь параллелограмма, построенного на векторах и .
с. Будут ли вектора , , линейно зависимыми.
IV. Плоскость
проходит через точки
и
перпендикулярно плоскости
.
Найти точку пересечения прямой
с плоскостью
.
V. 
.
VI. 
.
VII.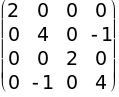 
.
Вариант №19
I.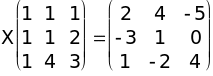 
.
II.а. 
.
II.б. 
.
III. Даны точки:
.
На векторах
построена пирамида. Вычислить:
а. Проекцию вектора на направление вектора .
б. Высоту
пирамиды, опущенную из вершины
.
с. Будут ли вектора и ортогональны.
IV. Прямая
проходит через точку
перпендикулярно прямым
и
.
Найти угол между прямой
и плоскостью
.
V. 
.
VI. 
.
VII.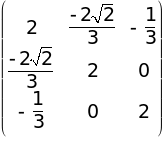 
.
Вариант №20
I.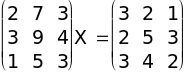 
.
II.а. 
.
II.б. 
.
III. На векторах
построен параллелепипед. Вычислить:
а. Проекцию
вектора
на направление вектора, противоположного
вектору
.
б. Площадь параллелограмма, построенного на веткорах и .
с. Объем параллелепипеда.
IV. Прямая
проходит через точку
перпендикулярно двум прямым
и
.
Найти точку пересечения прямой
с плоскостью
.
V. 
.
VI. 
.
VII.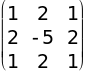 
.
Вариант №21
I. 
.
II.а. 
.
II.б. .
III. Даны точки:
.
На векторах
построена пирамида. Вычислить:
а. Косинус угла между векторами и .
б. Вектор, ортогональный векторам и и образующий с ними левую тройку векторов.
с. Объем пирамиды.
IV. Найти угол
между прямой
и плоскостью
,
проходящей через точки
,
,
.
V. 
.
VI. 
.
VII. 
.
Вариант №22
I. .
II.а. .
II.б. .
III. На векторах построен параллелепипед. Вычислить:
а. Проекцию вектора на направление, противоположное направлению вектора .
б. Высоту параллелепипеда, опущенную на грань .
с. Объем параллелепипеда.
IV. Плоскость проходит через прямую перпендикулярно плоскости . Найти расстояние от точки до плоскости .
V. .
VI. .
VII. .
Вариант №23
I. .
II.а. .
II.б. .
III. Даны точки: . Вычислить:
а. Косинус угла между векторами и .
б. Высоту треугольника , опущенную из вершины .
с. Являются ли вектора , , линейно зависимыми.
IV. Написать уравнение плоскости , проходящей через прямую параллельно прямой .
V. .
VI. .
VII. .
Вариант №24
I. .
II.а. .
II.б. .
III. Даны точки: . На векторах построена пирамида. Вычислить:
а. Проекцию вектора на направление вектора .
б. Будут ли вектора и коллинеарны.
с. Объем пирамиды.
IV. Прямая проходит через точку параллельно двум плоскостям и . Найти проекцию точки на прямую .
V. .
VI. .
VII. .
Вариант №25
I. .
II.а. .
II.б. .
III. На векторах построен параллелепипед. Вычислить:
а. Направляющие косинусы вектора .
б. Высоту параллелепипеда, опущенную на грань, образованную векторами и .
с. Объем параллелепипеда.
IV. Найти проекцию точки на плоскость , проходящую через прямую параллельно прямой .
V. .
VI. .
VII. .