
- •Головная программа
- •2. Управляющие подпрограммы
- •3. Подпрограммы генерирования реализации сп
- •3.2. Автономная подпрограмма istok1
- •4.1. Автономная подпрограмма razm1
- •6. Подпрогратя расчета статистически корреляционных моментов сп
- •6.1. Автономная подпрограмм коrm1
- •6.2. Автономная подпрограмма kormm
- •7.1. Автономная подпрограмма korf1
- •7.2. Автономная подпрограмма korf2
- •7.5. Автономная подпрограмма - функция func1
- •8. Подпрограмма расчета статистических hoрмированных функций спектральной плотности
- •8.1. Автономная подпрограмма formf1
- •8.2. Автономная подпрограмма spid1
- •8.3. Автономная подпрограмма spid2
- •8.4. Автономная подпгограмма spidm
- •8.5. Abtoномная программа spin1
- •9. Подпрогрмма расчета статистических функций плотности вероятности сп
- •9.1. Автономная программа formx1
- •9.2. Автономная программа formxm
- •9.3. Автононяая подпрограмма gist1
- •9.4. Автономная подпрограмма gist2
- •9.5. Автономная программа gistm
- •10. Подпрограммы расчета заданных /теоретических/ статистических характеристик сп
- •10.1. Автономная подпрограмма test1
- •11. Подпрограммы анализа точности
- •11.1. Автономная подпрограмма anal1
- •12. Запуск ппп.
3.2. Автономная подпрограмма istok1
Данная подпрограмма написана на алгоритмическом языке ФОРТРАН-4 и предназначается для проведения операции генерирования дискретизированной реализации стационарного некоррелированного многомерного /векторного/ СП, подчиняющегося заданному закону распределения из числа предусмотренных в подпрограмме.
В подпрограмме содержится обращение к автономным подпрограммам-функциям GAUSS, RELEY, EXPON.
Обращение к подпрограмме имеет вид:
CALL ISTOKM(X, N, M, JPLOV P1, P2, NPP, Z0).
Здесь:
X(N, M)- массив дискретизированной с постоянным шагом по временной координате Т реализации СП Х(Т);
N- число узлов в массиве Х, относящихся к одной составляющей векторного массива СП;
М- число составляющих векторного СП;
JPLOV - признак Jf вида функции плотности вероятности f(X) СП Х(Т); Jf [1,4] /равномерному закону распределения соответствует Jf = 1, нормальному закону распределения - Jf = 2, закону распределения Рэлея - Jf = 3, экспоненциальному закону распределения - Jf = 4/;
PI, P2 - параметры p1 и р2 функции f(Х);
NPP - число Npp предварительных прокруток алгоритма генерирования реализации СП Х(Т) на режиме "холостого хода" /к использованию рекомендуется значение этого параметра, составляющее примерно 10 % от величины параметра N/;
Z0 - начальное значение последовательности псевдослучайных чисел /любое целое положительное нечетное число, не превышающее 67108864/, Z0.
Функции плотности вероятности СП Х(Т) для различных законов распределения из числа рассматриваемых в программе записываются в форме:
при Jf = l
при Jf = 2

при Jf = 3
при Jf = 4
Операция вычисления значении дискретизированного СП Х(Т) в подпрограмме производится по следующим рекуррентным соотношениям, реализующим метод обратной функции распределения:
 ;
;
;
;

 ;
;

 ;
;

Под yi,j здесь понимается 1-ый элемент j-ой последовательности псевдослучайных чисел, распределенных по равномерному закону в интервале (0, 1), под выражением INT(А)- целая часть вещественного числа А, а под выражениями GAUSS(А), RELEY(A) и EXPON(А) - обратные -функции распределения соответственно нормального, рэлеевского и экспоненциального законов распределения, определяющие величину СП Х(Т), для которой функция распределения равна А.
3.3. АВТОНОМНАЯ ПОДПРОГРАММА - ФУНКЦИЯ GAUSS
Данная подпрограмма-функция написана на алгоритмическом языке ФОРТРАН-4 и предназначается для проведения операции вычисления значения СП, подчиняющегося нормальному закону распределения, которое соответствует заданному значению функции распределения этого процесса.
Обращение к подпрограмме-функции имеет вид:
Х = GAUSS(Y, P1, P2).
Здесь:
Х - искомое значение СП;
Y - заданное значение функции распределения СП;
PI, P2 - параметры р1- и p2 функции плотности вероятности СП, подчиняющегося нормальному закону распределения, при записи ее в форме:
Операция вычисления значения нормального СП, соответствующего заданному значению функции распределения этого процесса, проводится в подпрограмме-функции по следующим расчетным соотношениям, аппроксимирующим обратную функцию распределения:

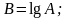


 3.4.
АВТОНОМНАЯ ПОДПРОГРАММА - ФУНКЦЯ RELEY
3.4.
АВТОНОМНАЯ ПОДПРОГРАММА - ФУНКЦЯ RELEY
Данная подпрограмма-функция написана на алгоритмическом языке ФОРТРАН-4 и предназначается для проведения операции вычисления значения СП, подчиняющегося рэлеевскому закону распределения, которое соответствует заданному значению функции распределения этого процесса,
Обращение к подпрограмме-функции имеет вид:
Х = RELEY (Y, PI. P2 ) ,
Здесь:
Х - искомое значение СП;
Y - заданное значение функции распределения СП;
PI, P2 - параметры р1- и p2 функции плотности вероятности СП, подчиняющегося нормальному закону распределения, при записи ее в форме:
Операция вычисления значения нормального СП, соответствующего заданному значению функции распределения этого процесса, проводится в подпрограмме-функции по следующим расчетным соотношениям, аппроксимирующим обратную функцию распределения:

3.5. АВТОНОМНАЯ ПОДПРОГРАММА-ФУНКЦИЯ EXPON
Данная подпрограмма-функция: написана на алгоритмическом языке ФОРТРАЕ-4 и предназначается для проведения операции вычисления значения СП, подчиняющегося экспоненциальному закону распределения, которое соответствует заданному значению функции распределения этого процесса.
Обращение к подпрограмме-функции имеет вид:
Х = EXPON(Y, PI, P2).
Здесь:
Х - искомое значение СП;
Y - заданное значение функции распределения СП;
PI, P2 - параметры р1- и p2 функции плотности вероятности СП, подчиняющегося нормальному закону распределения, при записи ее в форме:
Операция вычисления значении дискретизированного СП Х(Т) в подпрограмме производится по следующим рекуррентным соотношениям, реализующим метод обратной функции распределения:
 3.6.
АВТОНОМНАЯ ПОДПРОГРАММА KANON1
3.6.
АВТОНОМНАЯ ПОДПРОГРАММА KANON1
Данная подпрограмма написана на алгоритмическом языке ФОРТРАН-4 и предназначается для проведения операции генерирования дискретизированной реализации стационарного коррелированного одномерного /скалярного/ СП, подчиняющегося заданному закону распределения и обладающего корреляционной функцией заданного типа.
Обращение к подпрограмме имеет вид:
CALL KANON1 (X, N, Е, D, R0, NR0, А, В, С, F) .
Здесь:
X(N) - на входе в подпрограмму - массив случайных величин Нк, некоррелированных между собой, подчиняющихся заданному закону распределения и характеризующихся нулевым математическим ожиданием и единичной дисперсией, а на выходе из подпрограммы - массив сформированной дискретизированной с постоянным шагом по временной координате Т реализации СП Х(Т), обладающей статистическими характеристиками, близкими к заданным;
N- число узлов в массиве X;
Е, D - заданные значения математического ожидания и дисперсии генерируемого СП;
R0
(NRO)
- массив заданных значений нормированной
корреляционной функции
 генерируемого СП, соответствующих
равноотстоящим друг от друга /с шагом
дискретизации реализации СП/ значениям
ее аргумента
генерируемого СП, соответствующих
равноотстоящим друг от друга /с шагом
дискретизации реализации СП/ значениям
ее аргумента
 ;
;
NR0
- число узлов
 массиве R0;
массиве R0;
A (NRO, NRO) - рабочая матрица;
В, С, F (NRO) - рабочие массивы.
Операция вычисления значений дискретизированного СП Х(Т), соответствующего заданному закону распределения и обладающего корреляционной функцией заданного типа, производится в подпрограмме в рамках метода канонических разложений .
Согласно указанному
методу центрированная случайная функция
 разлагается
в ряд вида:
разлагается
в ряд вида:
 (1)
(1)
где под
 понимаются
случайные величины, некоррелированные
между собой и характеризующиеся нулевым
математическим ожиданием, а под
понимаются
случайные величины, некоррелированные
между собой и характеризующиеся нулевым
математическим ожиданием, а под
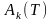 -
детерминированные координатные функции
времени.
-
детерминированные координатные функции
времени.
Простейший алгоритм
реализации, метода канонических
разложений для дискретной реализации
функции
 ,
определенной в равноотстоящих узлах,
формируется следующим образом:
,
определенной в равноотстоящих узлах,
формируется следующим образом:
 (2)
(2)
 (3)
(3)
 (4)
(4)

 (5)
(5)
 (6)
(6)
 (7)
(7)
Здесь:
 -
корреляционная функция СП Х(Т), задающая
/указывающая/ степень взаимосвязи между
сечениями этого процесса с координатами
ТК
и ТМ;
-
корреляционная функция СП Х(Т), задающая
/указывающая/ степень взаимосвязи между
сечениями этого процесса с координатами
ТК
и ТМ;
ВК - дисперсия случайной величины НК.
Использование
данного алгоритма целесообразно только
для случая формирования реализации
случайных функций, характеризующихся
относительно небольшим числом узлов
дискретизации N
и соизмеримостью длины реализации
с интервалом корреляции случайной
функции. Дело в том, что в противном
случае указанный алгоритм оказывается
неоправданно громоздким, так как при
этом приходится запоминать двумерный
массив координатных функций размером
 ,
большая часть которого заполнена
нулями.
,
большая часть которого заполнена
нулями.
В то же самое время при решении задач воспроизведения реализаций случайных функций зачастую приходится иметь дело с реализациями, содержащими большое число узлов /несколько тысяч или даже десятков тысяч/, а интервалы корреляции процесса при этом обычно оказывается на несколько порядков меньше длины реализации.
Если корреляционная функция воспроизводимой случайной функции задана в виде:
 (8)
(8)
а нормированная
корреляционная функция
 задана последовательностью своих в
общем случае ненулевых значений
задана последовательностью своих в
общем случае ненулевых значений
 ,
, ,
т.е.
,
т.е.
 (9)
(9)
где
-
шаг квантования реализации, то, как
следует из анализа соотношений (5) –
(7), для произвольного числа "к"
область ненулевых значений координатной
функции
 ограничена областью определения
ограничена областью определения
 .
Таким образом, координатная функция
.
Таким образом, координатная функция
 в
общем случае отлична от нуля только при
значениях М, принадлежащих интервалу
в
общем случае отлична от нуля только при
значениях М, принадлежащих интервалу
 .
.
Но тогда формула (7) преобразуется к виду:
 (10)
(10)
 (11)
(11)
где под выражением МАХ(А, В) понимается максимум из величин А и В.
Таким образом, для
формирования очередного к-ого значения
центрированной случайной функции
 достаточно иметь информацию о значениях
координатных функций
достаточно иметь информацию о значениях
координатных функций
 в узлах
в узлах
 и
дисперсией, что, в свою очередь, позволяет
построить систему простых рекуррентных
соотношений для расчета
,
и
дисперсией, что, в свою очередь, позволяет
построить систему простых рекуррентных
соотношений для расчета
,
 и
и
 .
.
С этой целью вводятся
в рассмотрение матрица А размерности
и массивы В, С и Р размерности N,
предназначенные для хранения
соответственно необходимых для проведения
расчетов значений координатных функций
,
дисперсии ВК,
случайной функции
и
среднеквадратических соотношений,
равных
 .
.
При к = 1:





При к
 2:
2:







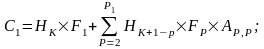



Если
 ,
то
,
то
 .
.
В описанном алгоритме расчета принимается, что реализация случайных величин НК имеет единичную дисперсию. Причем в результате проведения указанных операций значения случайной функции располагаются на месте случайных величин НК. Необходимо только после завершения указанного рекуррентного процесса сделать присвоение вида:
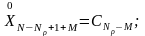
 .4.
ВСПОМАГАТЕЛЬНЫЕ ПОДПРОГРАММЫ
.4.
ВСПОМАГАТЕЛЬНЫЕ ПОДПРОГРАММЫ
Подпрограммы, включенные в данный раздел пакета, предназначаются, для выполнения следующих операций:
масштабирования элементов одномерного массива /подпрограмма RAZM1/;
масштабирования элементов многомерного массива /подпрограмма RAZMM/;
нахождения минимумома функционала методом формального поиска /подпрограмма FORM/.
