
- •Інститут економіки та нових технологій Кафедра прикладної математики та математичного моделювання
- •Передмова
- •І. Основні питання, що вивчаються в розділі „Функції багатьох змінних ”
- •Поняття функції багатьох змінних.
- •1.3. Послідовності точок в .
- •1.4. Означення функції багатьох змінних.
- •9.2. Найбільше та найменше значення функції в замкненій області. Іі. Основні теоретичні відомості. Приклади розв’язання задач
- •1. Поняття функції багатьох змінних
- •1.1. Евклідовий простір ( )
- •1.2. Множини точок в ( ).
- •1.3. Послідовності точок в ( )
- •Теорема 1
- •1.4. Означення функції багатьох змінних
- •Приклад 4
- •Розв’язання
- •Приклад 5
- •Розв’язання
- •3. Границя та неперервність функцій багатьох змінних
- •3.1. Границя функцій багатьох змінних
- •2.2. Неперервність функції багатьох змінних
- •Теорема 3
- •Теорема 4
- •3. Частинні похідні функції багатьох змінних
- •Приклади 10-11
- •Розв’язання
- •Розв’язання
- •Приклад 12
- •Розв’язання
- •4. Диференціал функції та його використання
- •Теорема 5
- •Приклад 13
- •Розв’язання
- •Приклад 14
- •Розв’язання
- •5. Диференціювання неявних функцій
- •6. Похідна за напрямом. Градієнт
- •Якщо використати теорему Лагранжа, то неважко показати, що (24)
- •Приклад 15
- •Розв’язання
- •7. Частинні похідні вищих порядків
- •Приклад 16
- •Розв’язання
- •8. Застосування частинних похідних в економічних задачах
- •9. Екстремум функції багатьох змінних
- •9.1. Локальний екстремум функції багатьох змінних
- •Теорема 6
- •Приклади 17-18
- •Розв’язання
- •Розв’язання
- •Має максимум, якщо або
- •Має мінімум, якщо або
- •Не має екстремуму, якщо
- •9.2. Найбільше та найменше значення функції в замкненій області
- •Приклад 21
- •Розв’язання
- •Ііі. Завдання для контрольної роботи. Завдання 1
- •Варіанти завдань:
- •Завдання 2.
- •Варіанти завдань:
- •Іv. Список використаної та рекомендованої літератури
Теорема 5
Якщо
частинні похідні функції
![]() існують в околі точки
і неперервні в самій точці
,
то функція
,
диференційована в цій точці.
існують в околі точки
і неперервні в самій точці
,
то функція
,
диференційована в цій точці.
Приклад 13
Знайти
диференціал функції:
![]()
Розв’язання
Знайдемо частинні похідні
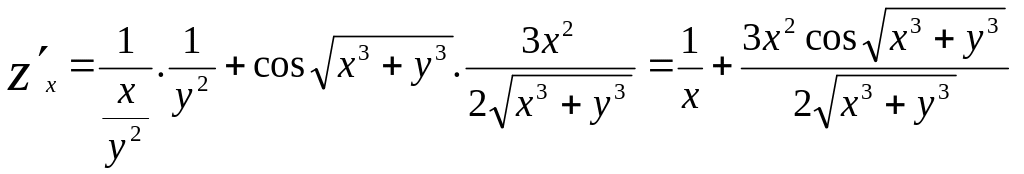 ,
,
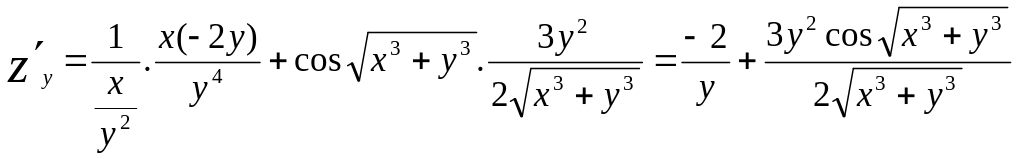
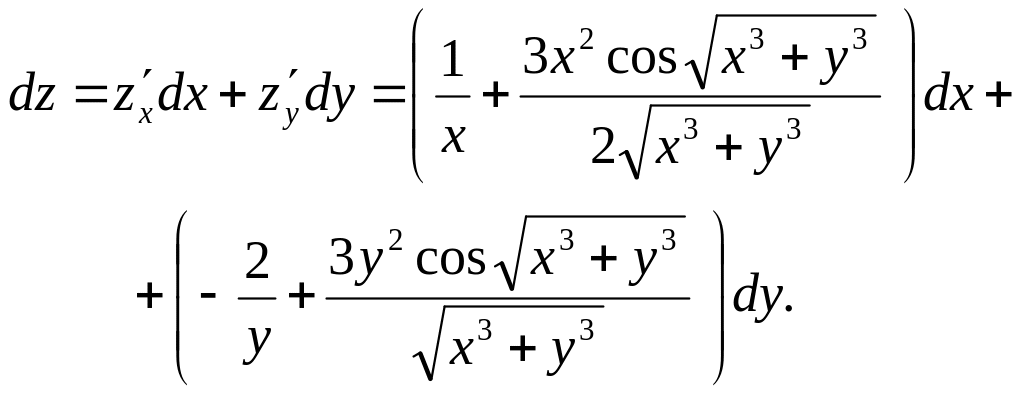
Як і для функції однієї змінної співвідношення (18) дозволяє знаходити наближене значення функції двох змінних. Дійсно оскільки
![]()
тому в силу (14)
![]() .
.
(21)
Формула (21) і дозволяє знаходити наближене значення функції двох змінних.
Зауваження
Формула (21) показує
що заміна повного приросту функції її
повним диференціалом привела до заміни
функції
в
околі точки
![]() лінійною функцією відносно
та
оскільки
лінійною функцією відносно
та
оскільки
![]() Геометрично це означає
що частина поверхні
замінюється відповідною частиною
дотичної площини до поверхні в точці
Геометрично це означає
що частина поверхні
замінюється відповідною частиною
дотичної площини до поверхні в точці
Приклад 14
Знайти наближене значення функції:
![]() в
точці
в
точці
![]() .
.
Розв’язання
Тут
![]() Послідовно обчислимо:
Послідовно обчислимо:
![]()
![]()
За
формулою (21), враховуючи, що
![]() дістанемо:
дістанемо:
![]()
5. Диференціювання неявних функцій
Якщо
рівняння
![]() ,
де
,
де
![]() – диференційована функція змінних x
і y,
визначає y
як функцію від x,
то похідну цієї неявно заданої функції
(за умовою, що
– диференційована функція змінних x
і y,
визначає y
як функцію від x,
то похідну цієї неявно заданої функції
(за умовою, що
![]() )
можна знайти за формулою
)
можна знайти за формулою
![]() .
Похідні вищих порядків знаходяться
послідовним диференціюванням отриманої
формули.
.
Похідні вищих порядків знаходяться
послідовним диференціюванням отриманої
формули.
Аналогічно,
якщо рівняння
![]() ,
де
,
де
![]() – диференційована функція змінних x,
y,
z,
визначає z
як функцію незалежних змінних x
та y
і
– диференційована функція змінних x,
y,
z,
визначає z
як функцію незалежних змінних x
та y
і
![]() ,
то частинні похідні цієї функції можна
знаходити за формулами:
,
то частинні похідні цієї функції можна
знаходити за формулами:
![]()
6. Похідна за напрямом. Градієнт
Нехай
функція
визначена в деякому околі точки
![]() ,
a
,
a
![]() – напрямок, що задається одиничним
вектором
– напрямок, що задається одиничним
вектором
![]() ,
де
,
де
![]()
![]() - кути, які утворює вектор
- кути, які утворює вектор
![]() з осями координат.
з осями координат.
Якщо
точка
перейде по напряму
в точку
![]() ,
то функція
одержить приріст у напрямі
,
тобто
,
то функція
одержить приріст у напрямі
,
тобто
![]() .
(22)
.
(22)
Оскільки
![]() то очевидно (див. Рис.3), що
то очевидно (див. Рис.3), що
![]() ,
,
![]() .
.

Рис.3.
Тому приріст функції у даному напрямі перепишемо у вигляді:
![]() .
.
Означення
22.
Похідною
![]() за напрямом
функції двох змінних
називається границя відношення приросту
функції в цьому напрямі до величини
переміщення
за напрямом
функції двох змінних
називається границя відношення приросту
функції в цьому напрямі до величини
переміщення
![]() при прямуванні її до нуля, тобто
при прямуванні її до нуля, тобто
![]() .
(23)
.
(23)
Похідна – характеризує швидкість зміни функції в напрямі .
Зрозуміло,
що частинні похідні
![]() та
та
![]() є похідні за напрямами паралельними
осям Ox
та Оy
відповідно.
є похідні за напрямами паралельними
осям Ox
та Оy
відповідно.
Якщо використати теорему Лагранжа, то неважко показати, що (24)
Означення
23.
Градієнтом
![]() функції
називається
вектор
з координатами
функції
називається
вектор
з координатами
![]() .
.
Враховуючи,
що
![]() ,
,
![]() праву частину (24) можемо записати у
вигляді
скалярного добутку:
праву частину (24) можемо записати у
вигляді
скалярного добутку:
![]() .
(25)
.
(25)
Звідси
випливає, що похідна за напрямом є
скалярний добуток градієнта
![]() і одиничного вектора, який задає напрям
і одиничного вектора, який задає напрям
![]() .
.
Скалярний
добуток двох векторів (25) максимальний,
якщо вони мають однаковий напрям. Тому
градієнт
функції
в даній точці характеризує напрям
максимальної швидкості зміни функції
в цій точці.
Градієнт записують через його координати
![]() ,
а
його довжина
,
а
його довжина
![]() дає
величину максимальної швидкості зміни
функції в точці
.
дає
величину максимальної швидкості зміни
функції в точці
.
