7.4.3. Вычисление объёма тела

Вычисление объема тела по известным площадям его поперечных

сечений

Пусть имеется тело объема V. Площадь любого поперечного сечения тела S, известна как непрерывная функция S = S(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки х_i разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [x_i-1, x_i] функция S(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно M_i и m_i.

Рис. 7.18

Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны M_ix_i и m_ix_i здесь x_i = x_i+1 - x_i.

Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно и .

При стремлении к нулю шага разбиения , эти суммы имеют общий предел:

.

Таким образом, объем тела может быть найден по формуле:

. (7.13)

Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию S(x), что весьма проблематично для тел сложной формы.

Объём тела вращения

Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения (рис. 7.19).

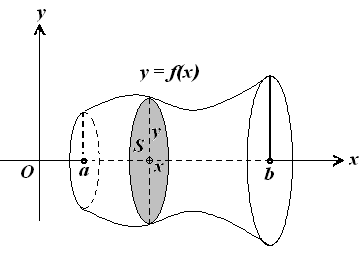
Рис. 7.19.

Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох ( ), есть круг с радиусом y = f(x). Следовательно, площадь поперечного сечения S(x) = π y².

Применяя формулу (7.13) объёма тела по площади поперечных сечений, получаем

. (7.14)

Пример. Определить объём тела, образованного вращением фигуры, ограниченной линиями y = x² , x = 1, x = 2 (рис. 7.20).

Рис. 7.20.

Решение. По формуле (7.14) находим

= .

7.4.4. Механические приложения определённого интеграла\

Центр тяжести плоской фигуры

Согласно закону всемирного тяготения все тела притягиваются к Земле с силой, пропорциональной массе тела ( m - масса тела и g = 9,81 м/с² ), эта сила называется весом тела (силой тяжести).

При рассмотрении равновесия и движения тел сложной формы важно знать положение центра тяжести этого тела.

Рассмотрим определение положения центра тяжести материальной пластины АВВ₁А₁ в виде криволинейной трапеции, ограниченной сверху кривой АВ, которая задана явным уравнением у = у(х), и линиями х = а, х = b ( a < b) и у = 0 (Рис. 7.21).

Рис. 7.21

Предположим, что поверхностная плотность материала пластины постоянна, т.е. фигура однородна. Можно для определенности считать, что удельный вес материала пластины равен 1 ( γ = ρ g = 1, ρ – плотность материала), тогда масса пластины или её любой части измеряется соответствующей площадью.

Для определения положения центра тяжести проведём разбиение рассматриваемой пластины на вертикальные полосы с основаниями i = 1,2,…,n ( ). Центр тяжести каждой полосы определяется координатами

, ,

где и - координаты точки кривой ( = y ( ) ).

Центром тяжести рассматриваемой однородной пластины АВВ₁А₁ , также как любого другого тела, обладает тем свойством, что его положение не зависит от поворота данной пластины на любой угол по отношению к вертикали. Как показано в курсе теоретической механики координаты центра тяжести тела определяется формулами

, , (7.15)

когда количество разбиений стремится к бесконечности, а длина элементов разбиения . В формулах (7.15) - площадь i – ой полосы разбиения

( , ).

Переходя к пределу в формулах (7.15), когда и , соответствующие суммы являются интегральными, поэтому координаты центра тяжести криволинейной трапеции определяется формулами

, , (7.16)

где y = y(x) – уравнение кривой АВ.

Замечания. 1. Если плоская фигура имеет ось или центр симметрии, то центр тяжести такой фигуры находится на оси или в центре симметрии.

2. Если тело состоит из частей, центры тяжести которых известны, то центр тяжести составной фигуры определяется по формулам

, ,

здесь k – количество составных частей; S_i и х_i, у_i – соответственно площадь и координаты центра тяжести i-ой части. Если же плоская фигура имеет отверстия, то центр тяжести этой фигуры определяется по этим же формулам, однако площади, соответствующие отверстиям должны быть отрицательными.

Пример. Определить координаты центра тяжести четверти круга (х, у > 0) . Изобразим данную плоскую фигуру

Площадь четверти круга .

Определяем интегралы числителей формул (7.16) (эти интегралы называются статическими моментами)

,

.

Таким образом, координаты центра тяжести четверти круга равны

, .

Задачи для самостоятельного решения.

Найти координаты центра тяжести фигуры, ограниченной линиями:

1) , x = 0, y = 0 . 2) x = 0, x = , y = 0, y = cos x.

3) y = 2 x – x² , y = 0 . 4) y = , y = sin x.

Работа и мощность силы

Для характеристики действия, оказываемого на тело при некотором его перемещении, вводится понятие о работе силы. Рассмотрим прямолинейное движение тела M вдоль оси Ох под действием переменной силы F(x) из положения х₀ в положение х₁ (рис. 7.22). Примером переменной силы, зависящей от перемещения х , является сила упругости пружины

, (7.17)

где с – жёсткость пружины, х – деформация этой пружины. Другими примерами таких сил являются сила всемирного тяготения, сила Кулона взаимодействия между зарядами, эти зависят от расстояния между телами (зарядами).

Рис. 7.22.

Введём сначала понятие об элементарной работе силы F на бесконечно малом перемещении

.

Работа силы на любом конечном перемещении как интегральная сумма соответствующих элементарных работ равна

. (7.18)

Единицей измерения работы в системе СИ является джоуль (1 дж = 1 н м).

Мощность. Мощностью называется величина, определяющая работу, совераемую силой в единицу времени. Если работа совершается равномерно, то мощность

, (7.19)

где t – время, в течение которого произведена работа. В общем случае

, (7.20)

где v – скорость движения тела.

Единицей измерения мощности в системе СИ является ватт (1 вт = 1 дж/сек).

Работу, произведенную машиной, измеряют произведением её мощности на время работы. Отсюда возникла употребительная в технике единица измерения работы киловатт-час.

Примеры. 1) Вычислить работу, которую необходимо затратить, чтобы поднять тело массы m с поверхности Земли на высоту h (радиус Земли R = 6400км). С помощью полученного результата определить вторую космическую скорость (скорость, при которой вертикально поднимающееся тело может подняться на любую высоту).

Решение. На ракету, имеющую массу m, по закону всемирного тяготения действует сила , где G – гравитационная постоянная; M – масса Земли; m – масса ракеты; x – расстояние ракеты до центра Земли, = 9,81 м/с² - ускорение свободного падения.

Искомая работа силы тяготения при выводе ракеты с поверхности Земли на высоту h равна

или, учитывая значение ускорения свободного падения, имеем

В то же время работа равна изменению кинетической энергии ракеты

, учитывая, что стартовая кинетическая энергия равна нулю, а V – скорость ракеты на высоте h над поверхностью Земли. Таким обра-зом, скорость ракеты V на высоте h определяется из уравнения

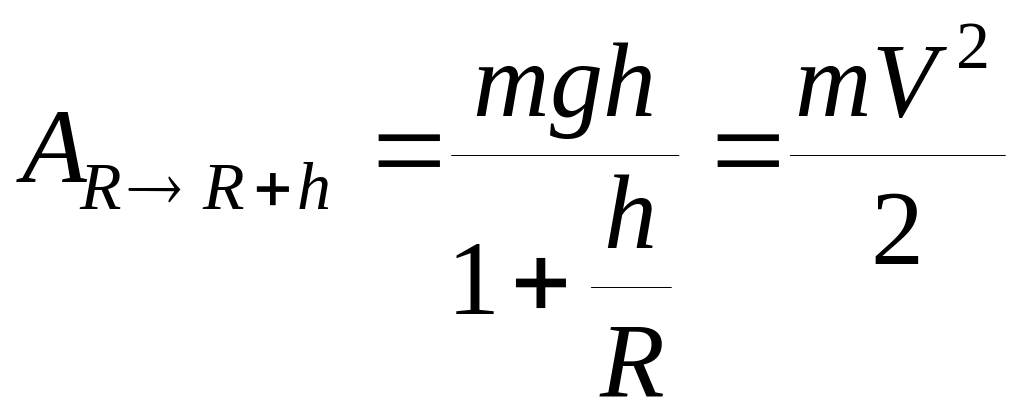, откуда .

Чтобы рассчитать вторую космическую скорость, которую надо сообщить ракете у поверхности Земли для преодоления земного притяжения, нужно перейти пределу h → ∞ в последнем выражении

(м/с).

2) Вычислить работу, которую надо затратить, чтобы растянуть пружину, находящуюся в положении равновесия, на 10 см. Известно, что при растяжении пружины на 1 см сила натяжения равна 5 н.

Решение. Упругая сила, с которой действует пружина на тело, подчиняется закону Гука, согласно которому F =с x, где с – жёсткость пружины, а х – удлинение пружины. Из условия задачи находим жёсткость пружины с. Так как при растяжении пружины на 0,01 м сила упругого натяжения равна 5 н, то 5н = с ∙0,1 м. Следовательно, с = 500 н /м и сила упругости пружины равна F(x) = 500 x , н

Искомая работа силы упругости при растяжении пружины на 10 см = 0,1 м вычисляется по формуле: