7.4.2. Определение длины дуги плоской кривой

Прямоугольные координаты

Пусть в прямоугольных координатах задана плоская кривая АВ, уравнение которой , где . Если и непрерывны, то такие кривые называются гладкими. Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число сторон ломаной неограниченно возрастает, а длина набольшей из сторон ломаной стремится к нулю.

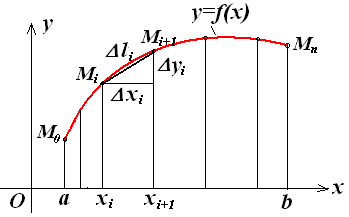
Рис. 7.16.

Длина ломаной линии, которая соответствует дуге M₀M_n , может быть найдена как сумма , где - длина стороны ломаной на участке (рис. 7.16). Тогда длина дуги M₀M_n равна .

Из геометрических соображений: 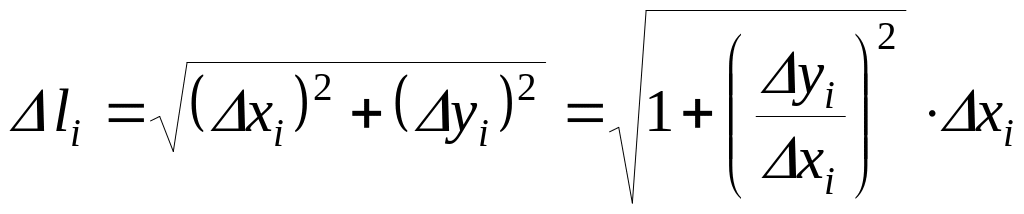, но в то же время .

Тогда . Т.е. длина дуги M₀M_n при изменении х от а до b равна

. (7.9)

Пример. Вычислить длину дуги кубической параболы , находящейся между точками и .

Так как , то . Поэтому искомая длина дуги согласно формуле (7.9) определяется следующим образом

= .

Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции, из формулы (7.9) получаем

=

= ,

где х = x(t), a = x(α) и у = у(t), b=y(β). Таким образом, если уравнение кривой задано в параметрической форме, то длина кривой находится по формуле

. (7.10)

Пример. Найти длину первой арки циклоиды

Находим производные и . По формуле (7.10) длина арки циклоиды

=

=

= .

Если задана пространственная кривая, и х = x(t), у = y(t) и z = z(t), то

. (7.11)

Полярные координаты

Пусть кривая задана в полярных координатах , , причем функция и непрерывны на отрезке [α, β]. Воспользуемся формулами связи между полярными и декартовыми координатами , , тогда считая угол φ параметром, можно задать уравнение кривой в параметрической форме

и длину кривой находим по формуле (7.10), выполнив соответствующие преобразования

Поэтому =

= .

В результате длина кривой определяется формулой

. (7.12)

Пример. Найти длину кардиоиды . Кардиоида, изображённая на рисунке

Рис. 7.17

может быть получена как траектория точки окружности С₁, катящейся без скольжения по окружности С того же радиуса а. Когда φ пробегает промежуток (-π, +π), кардиоида описывается полностью. Длина её согласно (7.12) равна

Таким образом, длина кардиоиды равна восьмикратному диаметру производящего круга.