
- •7. Определённый интеграл
- •7.1.Понятие определённого интеграла
- •7.2. Вычисления определённого интеграла
- •7.3. Вычисление определённого интеграла с помощью пакета Maxima
- •7.4. Применение определённого интеграла
- •7.4.1. Вычисление площадей плоских фигур
- •7.4.2. Определение длины дуги плоской кривой
- •7.4.3. Вычисление объёма тела
- •7.5. Несобственные интегралы
- •7.6. Вычисление несобственных интегралов в среде Maxima
7. Определённый интеграл
7.1.Понятие определённого интеграла
Пусть на отрезке [a, b] задана непрерывная функция y = f(x). Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками.
x0 < x1 < x2 < … < xn
Тогда x1 – x0 = x1, x2 – x1 = x2, … ,xn – xn-1 = xn – длины частных отрезков.
На
каждом из полученных частных отрезков
[xi-1,
xi],
i
= 1, 2,…, n
выберем произвольную точку
![]() и найдем значение функции в этой точке,
т.е. f(сi
) (см.
рис. 7.1).
и найдем значение функции в этой точке,
т.е. f(сi
) (см.
рис. 7.1).
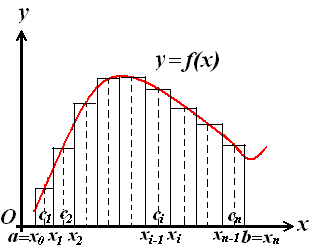
Рис. 7.1.
Составим выражение Sn , которое называется интегральной суммой для функции y = f(x) на отрезке [a, b].
Sn
= f(c1)x1
+ f(c2)x2
+ … + f(cn)xn
=
![]() .
.
Обозначим
λ
длину наибольшего частичного отрезка:
![]() (i
= 1, 2,…, n).
Найдём предел интегральной суммы, когда
(i
= 1, 2,…, n).
Найдём предел интегральной суммы, когда
![]() так, что
так, что
![]() .
.
Если
при любых разбиениях отрезка [a,
b]
на частичные таких, что maxxi
0 и произвольном
выборе точек сi
интегральная сумма
![]() стремится к пределу I
, то это число
называется определенным
интегралом
от функции y=f(x)
на отрезке [a,
b]
и обозначается
стремится к пределу I
, то это число
называется определенным
интегралом
от функции y=f(x)
на отрезке [a,
b]
и обозначается
![]()
Таким
образом,
![]() =
=
![]() .
(7.1)
.
(7.1)
Числа
а
и b
называются соответственно нижним
и верхним пределами
интегрирования, х
– переменной
интегрирования,
[a,
b]
– отрезком
интегрирования,
f(x)-
подынтегральной функцией,
![]() -
подынтегральным выражением.
-
подынтегральным выражением.
Функция у
= f(x),
для которой на отрезке [a,
b]
существует определённый интеграл
![]() называется интегрируемой
на этом отрезке.
называется интегрируемой
на этом отрезке.
Из рисунка 7.1. видно, что сумма произведений Sn = равна площади ступенчатой фигуры и приближённо равна площади S криволинейной трапеции:
S ≈ Sn = .
С уменьшением всех величин xi криволинейной трапеции ступенчатой фигурой увеличивается. Поэтому за точное значение площади криволинейной трапеции принимается предел S , к которому стремится площадь ступенчатой фигуры Sn , когда n неограниченно возрастает так, что :
![]() =
,
то есть S
=
.
=
,
то есть S
=
.
Таков геометрический смысл определённого интеграла.
Теорема (Коши). Если функция у = f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Существуют и иные теоремы математического анализа, определяющие классы функций, интегрируемых на отрезке [a, b]. В частности таковыми являются:
непрерывные на отрезке [a, b] функции;
ограниченные на отрезке [a, b] функции, имеющие конечное число точек разрыва;
монотонные на отрезке [a, b] функции.
Основные свойства определённого интеграла
Рассмотрим основные свойства определённого интеграла, считая подынтегральную функцию интегрируемой на отрезке [a, b]
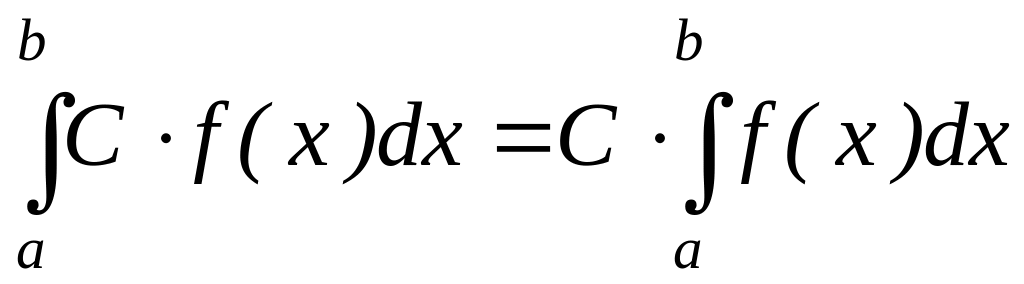 (С
– const)
, т.е. постоянный
множитель С можно выносить за знак
определённого интеграла.
(С
– const)
, т.е. постоянный
множитель С можно выносить за знак
определённого интеграла.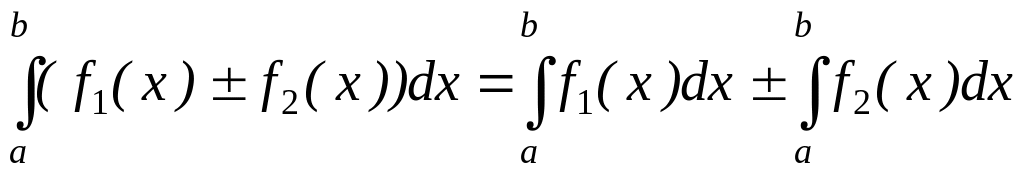 ,
т.е. интеграл
от суммы (разности) равен сумме (разности)
интегралов.
,
т.е. интеграл
от суммы (разности) равен сумме (разности)
интегралов.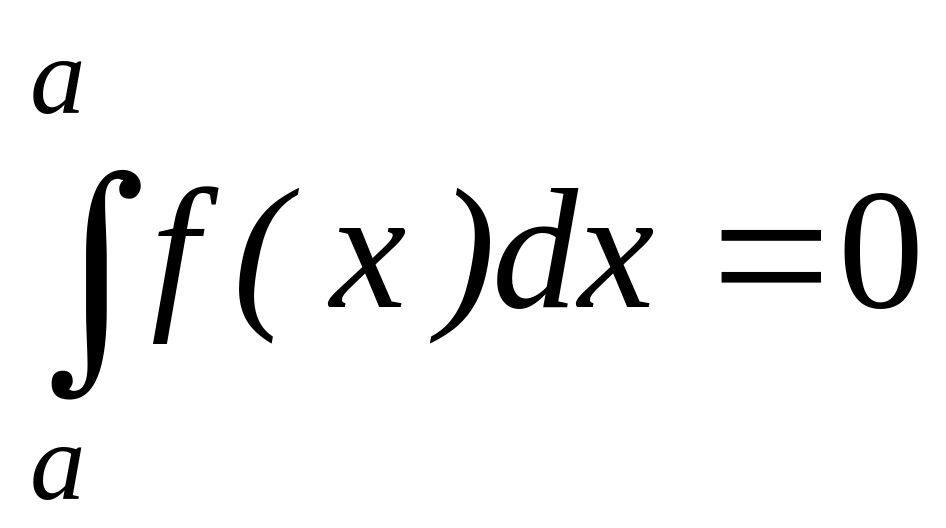 .
.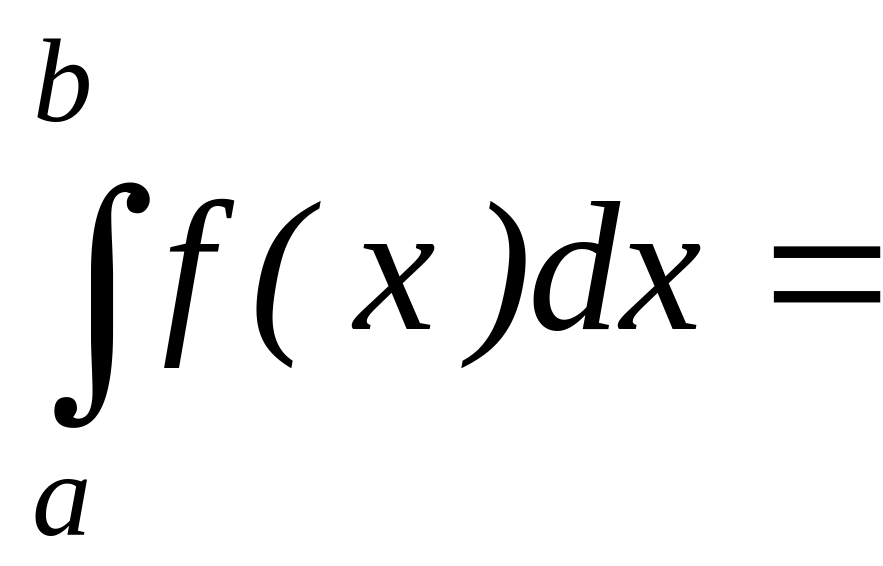
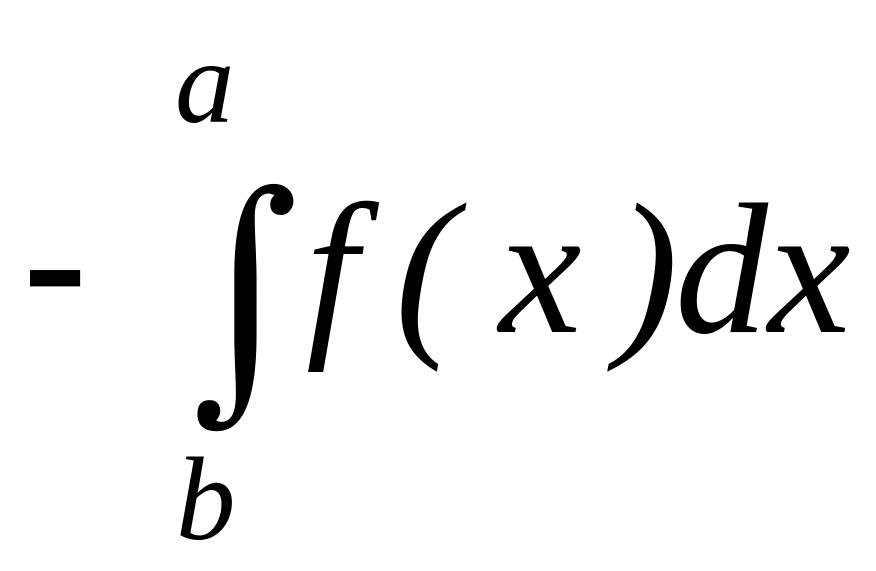 .
.
5) Для произвольных чисел a, b, c справедливо равенство:
![]() ,
т.е. интеграл
по всему отрезку равен
,
т.е. интеграл
по всему отрезку равен
сумме интегралов по частям этого отрезка.
Если функция f(x) сохраняет знак на отрезке [a, b], где a < b, то интеграл
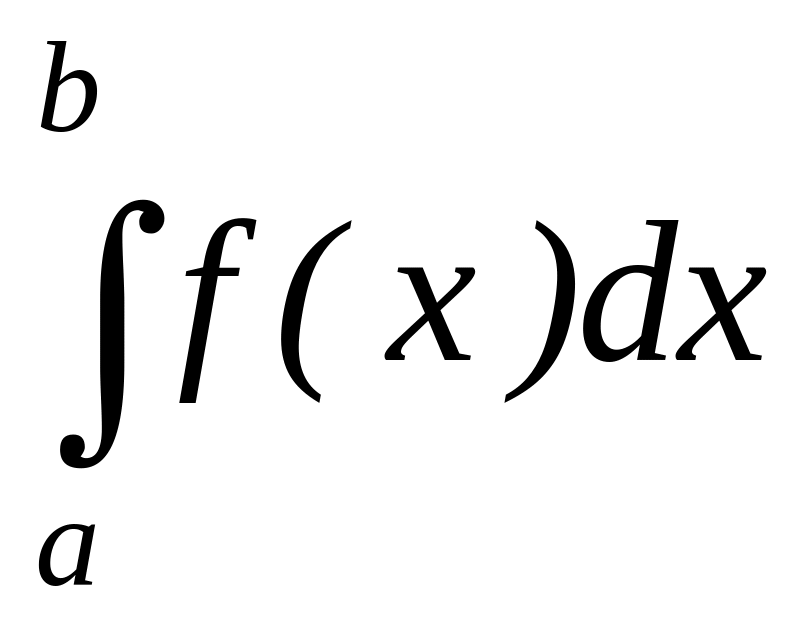 имеет тот же знак, что и функция. Так
если
имеет тот же знак, что и функция. Так
если
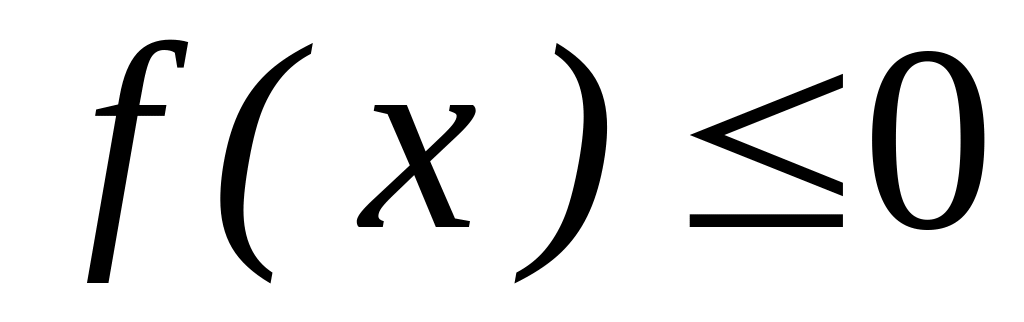 на отрезке
[a,
b]
, то
на отрезке
[a,
b]
, то
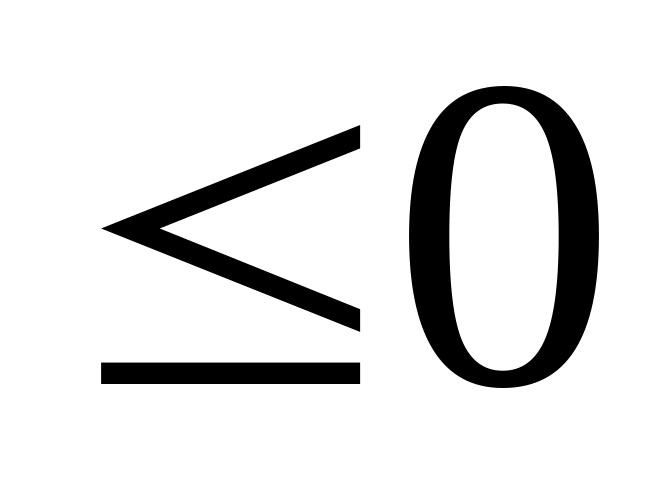 .
.Если f(x) (x) на отрезке [a, b] (a < b), то
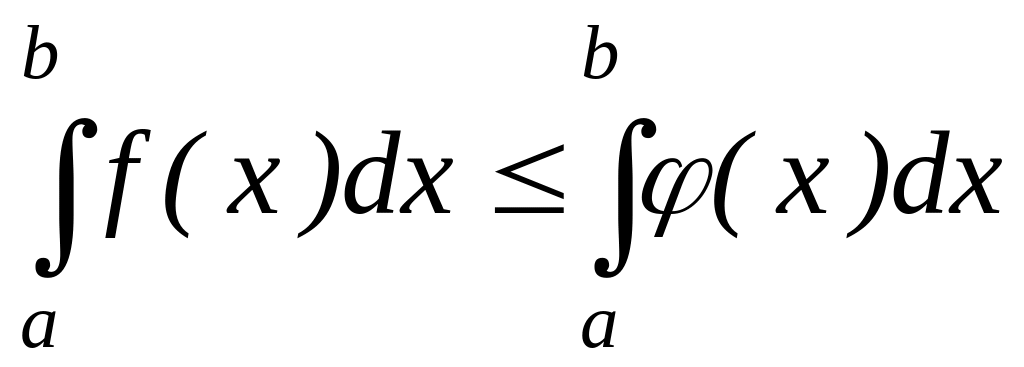 ,
т.е. неравенство
между непрерывными функциями на отрезке
[a,
b]
(a
< b)
можно
интегрировать.
,
т.е. неравенство
между непрерывными функциями на отрезке
[a,
b]
(a
< b)
можно
интегрировать.Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b] (a < b), то:
![]()
Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка
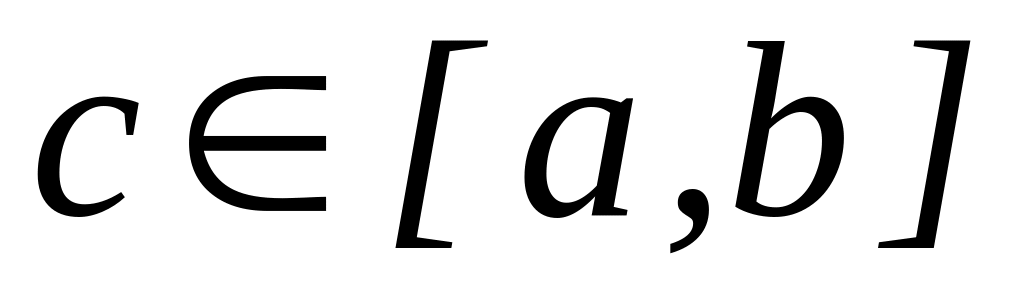 такая, что
такая, что
![]() .
.
Доказательство: В соответствии со свойством 8:
или
![]() .
Обозначим
.
Обозначим
![]() .
.
т.к.
функция f(x)
непрерывна на отрезке [a,
b],
то она принимает на этом отрезке все
значения от m
до М.
Другими словами, существует такое число
с
[a,
b],
что
= f(с),
т.е.
![]() или
.
Теорема доказана.
или
.
Теорема доказана.
10) Производная определённого интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом
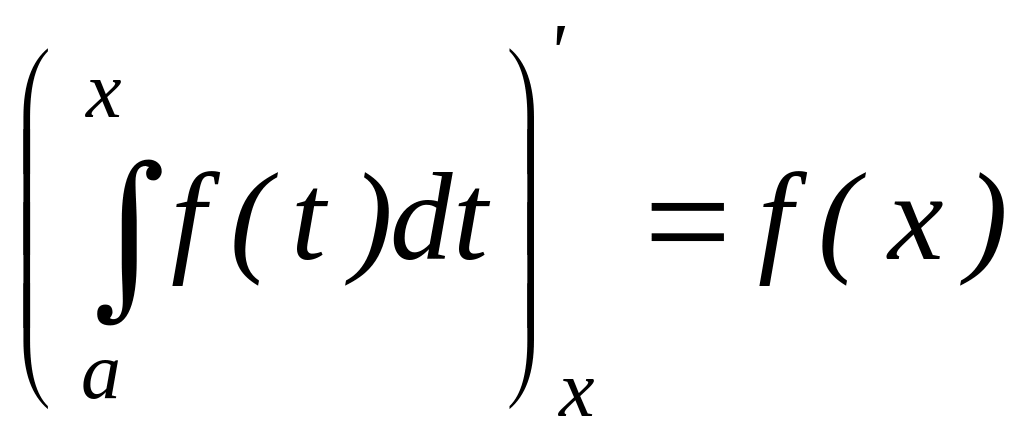
Доказательство:
пусть функция у
= f(x)
интегрируема на отрезке [a,
b].
Вводится обозначение
![]() , здесь
, здесь
![]() .
Рассмотрим три точки отрезка [a,
b]:
а , х, х + Δх
(
.
Рассмотрим три точки отрезка [a,
b]:
а , х, х + Δх
(![]() )
и определим разность
)
и определим разность
![]() .
По свойству 5 определённых интегралов
первый интеграл правой части можно
представить в виде
.
По свойству 5 определённых интегралов
первый интеграл правой части можно
представить в виде
суммы
![]() .
В результате
.
В результате
![]() .
.
По
теореме о среднем (свойство 9)
![]() ,
,
![]() .
.
Далее
вычислим производную функции
![]()
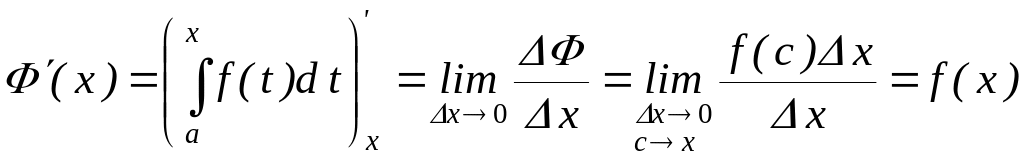 .
.
