1.2.3. Формула полной вероятности и формула Байеса

На практике часто возникают ситуации, когда требуется определить вероятность события В, которое может произойти с одним из несовместных событий A_i, образующих полную группу событий (A_i называются гипотезами). Для вычисления такой вероятности применяется формула полной вероятности:

Здесь Р(В/A_i) – условные вероятности события В.

Доказательство. Представим событие B в виде суммы несовместных событий: . Тогда .

Задача 1. В двух районах области, первый из которых в два раза по численности больше второго, доля пенсионеров составляет, соответственно, 0,3 и 0,21. Это условные вероятности того, что случайно взятый житель из первого, соответственно, второго района, является пенсионером. Надо определить, какую долю будут составлять пенсионеры в районе после их объединения.

Обозначим A₁ – событие, состоящее в том, что случайно взятый житель из объединенного района ранее жил в первом районе. Аналогично – А₂. Очевидно, что Р(А₁)=2/3, Р(А₂)=1/3. Тогда доля пенсионеров в объединенном районе определится по формуле полной вероятности: Р(В)=

Условие данной задачи, как и многих других, можно легко перевести на язык урновой схемы, если под районами понимать урны, а под пенсионерами, например, – белые шары.

Формула Байеса: ,

где – априорные вероятности гипотез A_i (i=1,2,…n), – апостериорные вероятности (они условные) гипотез A_k , т. е. уточненные после получения информации о том, что событие B произошло. Очевидно, что =1. Формула Байеса следует из равенства (левая и правая части равны Р(А_kВ)):

, если заменить .

Задача 2. Пусть один из жителей объединенного района (см. предыдущую задачу) попал в реанимацию. Известно лишь, что он – пенсионер. Какова вероятность того, что он – житель первого из объединенных районов?

Эта вероятность определяется по формуле Байеса:

.

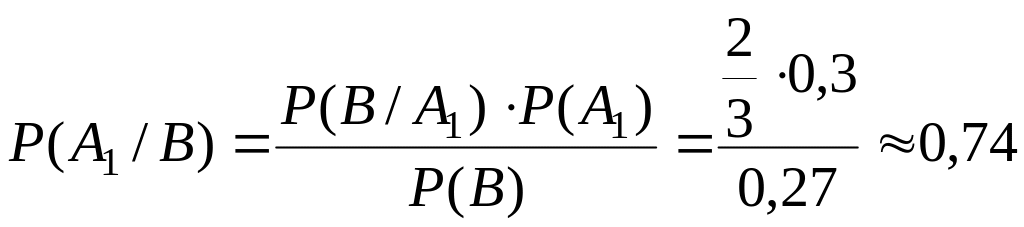Применение формулы Байеса может дать большой эффект и в тех случаях, когда нельзя обойтись без использования экспертной информации. Надо лишь грамотно организовать получение экспертных оценок и иметь экспертов, имеющих вероятностное мышление. Эксперты обычно пытаются оценивать сразу апостериорные вероятности. Но в этом случае для получения достаточно точных оценок требуются широко эрудированные эксперты, что является обычно большой редкостью. Гораздо чаще встречаются эрудированные узкие специалисты. Одни из них способны достаточно точно оценить априорные вероятности, другие – условные. Формула Байеса позволяет объединить всю эту информацию и в результате получить гораздо более точные оценки апостериорных вероятностей.

Задача 3. При расследовании дела об ограблении с убийством было установлено, что это мог сделать один из трех рецидивистов. По оценке экспертов (с участием участкового милиционера) вероятности того, что на ограбление пошел i-ый рецидивист (i=1,2,3), соответственно, равны: Р(А₁)=1/2, Р(А₂)=1/4, Р(А₃)=1/4. По оценке других экспертов (психологов с участием работников колоний, в которых отбывали наказание рецидивисты) вероятности того, что i-ый рецидивист мог совершить убийство, если он пошел на ограбление, равны: Р(В/A₁)=2/5, Р(В/A₂)=1/6, Р(В/A₃)=1/5. Определить вероятности того, что преступление совершил i-й рецидивист.

Последнее предложение можно перефразировать следующим образом. Надо определить вероятности того, что i-ый рецидивист пошел на ограбление, если было совершено убийство. Это апостериорные вероятности гипотез А_i. Они должны определяться по формуле Байеса. В частности, при i=1 имеем: