§ 5. Соответствие активов и пассивов.

В общем базисном контексте, соответствие активов и пассивов компании требуют, чтобы активы были выбраны таким образом, чтобы сделать их равно ответственными за влияние которое воздействует на них. В широком смысле, соответствие включает соответствие в терминах наличности и степени связи с инфляцией. Мы будем рассматривать активы и пассивы в денежных терминах.

Пассивы базиса – это суммы по контракту, которые ценные бумаги выплачены в будущем. Пусть - пассив в момент t (т.е. деньги, кот. Ц.б. вы­плачены в это время). Пусть - деньги которые должна получить компания в момент t за свои деловые операции, включая любые инвестиционные по­ступления на это время. Определим чистые пассивы – расходы в момент t: (1)

Чистые пассивы дела – это суммы { }. В обозначения 4.1:

Рассмотрим дискретный случай.

Пример10.5.1. Life-офис выпустил 20-летние погашаемые акции 10 лет назад с застра­хованной суммой $10000 и ежегодными премиями $288.02. Вычислить чистые пассивы { }.

Решение. =288.02 t = 1,2,…,9 (измеряем время в годах от настоящего)

=10000 t=10

Следовательно:

Поступления в момент t на инвестиции компании, либо капитальные, либо процентные, либо и те и другие называются asset-proceeds и обозначаются . Предполагаем в начале, что и что активы-поступления такие, что

(2)

В этом случае говорят, что ………….(matched). Если чистый поток наличности иногда положительный иногда отрицательный, абсолютное соответствие невозможно. Текущая стоимость чистых пассивов:

(3)

активов:

(4)

Предполагая далее, что будет постоянной , то

(5)

Этого будет достаточно, чтобы встретить чистые пассивы в будущем. На практике это предположение нереалистично. Степень защиты от изменения в процентных ставках можно получить используя принцип иммунизации.

§ 6. Теория иммунизации Redingona.

Рассмотрим финансовый институт, для определённости life-office, который имеет чистые пассивы-расходы и активы-доходы в t-м году. Текущая интенсивность и (1)

В дальнейшем активы-доходы могут изменяться и удовлетворяющие следующим дополнительным условиям

(2)

(3)

Если (1)-(3) выполняется, то , когда и имеет точку экстремума здесь. Т.о. существует окрестность т.ч., если δ лежит внутри, но неравно , то .

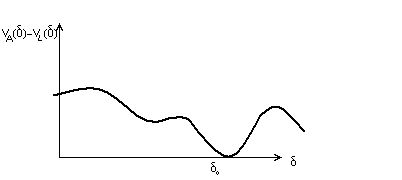
Инвестор, инвестиции которого удовлетворяют (1)-(3), сделал иммунизацию против малых изменений в процентной ставке. Обсудим, как условия (1)-(3) могут быть интерпретированы на практике. Т.к. , то уравнения (1) и (2) эквивалентны.

по интенсивности (5) по интенсивности (6)

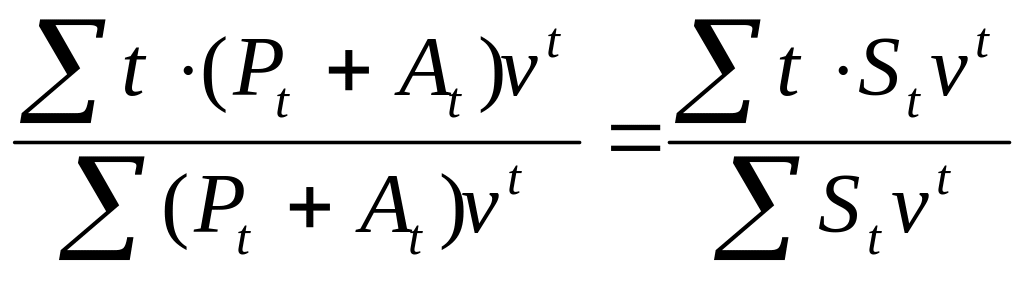по интенсивности (7)