
§ 4. Volatility ценных бумаг с фиксированным процентом.
Рассмотрим единственную номинальную
сумму акции с фиксированным процентом,
который приносит процент D
ежегодно и погашается через n
лет по цене R. Пусть
![]() и текущая цена акции равна текущей
стоимости, от интенсивности
за год будущих процентных и капитальных
выплат. Предположим, что у инвестора,
который купил акцию, все будущие чистые
потоки наличности положительны. Тогда:
и текущая цена акции равна текущей
стоимости, от интенсивности
за год будущих процентных и капитальных
выплат. Предположим, что у инвестора,
который купил акцию, все будущие чистые
потоки наличности положительны. Тогда:
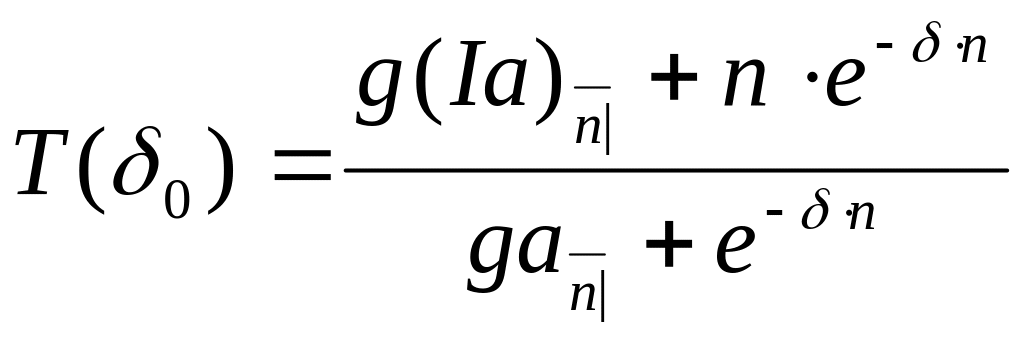 (1)
(1)
В частном случае, когда g
=
![]() ,
где
,
где
![]() связан с
связан с
![]() :
:
![]() по ставке
(2)
по ставке
(2)
Если в (1)
![]() ,
то:
,
то:
![]() по ставке
(3)
по ставке
(3)
Заметим, что zero-coupon bond: g = 0,
![]() (4)
(4)
Предположим, что процент выплачиваться непрерывно. Из (2.4) следует:
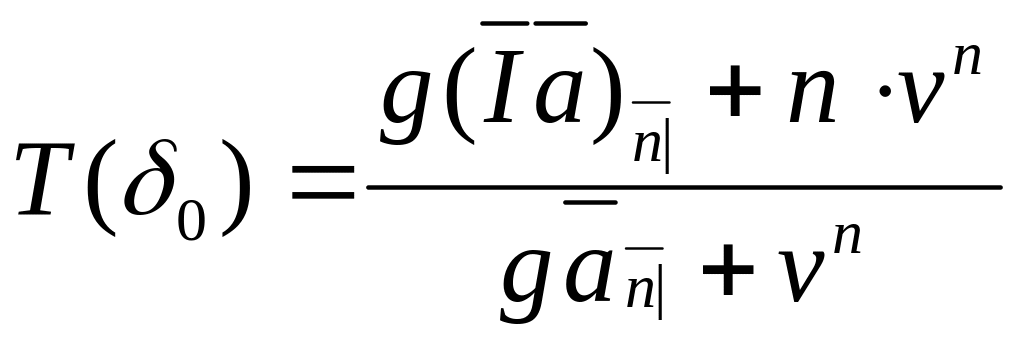 с интенсивностью
(5)
с интенсивностью
(5)
Сначала покажем, что для фиксированного n, volatility убывает с ростом g:
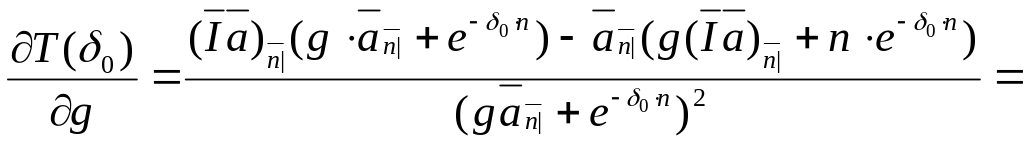
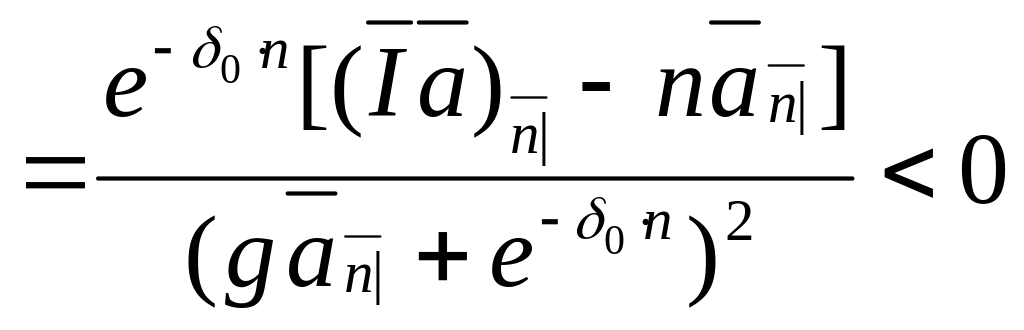
т.к.
![]()
Из (5) следует:
![]() (6)
(6)
![]() (7)
(7)
Можно показать:
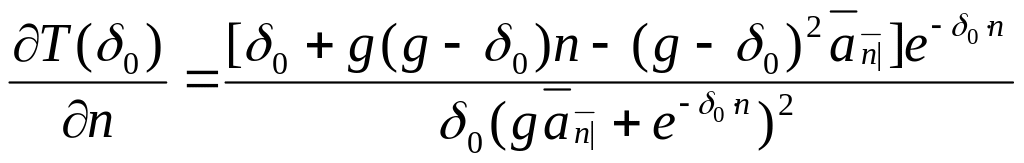
и следовательно знак
![]() тот же, что и у :
тот же, что и у :
![]() т.к.
т.к.
![]() - неотрицательно возрастающая
неограниченная функция от n,
имеем следующие результаты:
- неотрицательно возрастающая
неограниченная функция от n,
имеем следующие результаты:
Если g
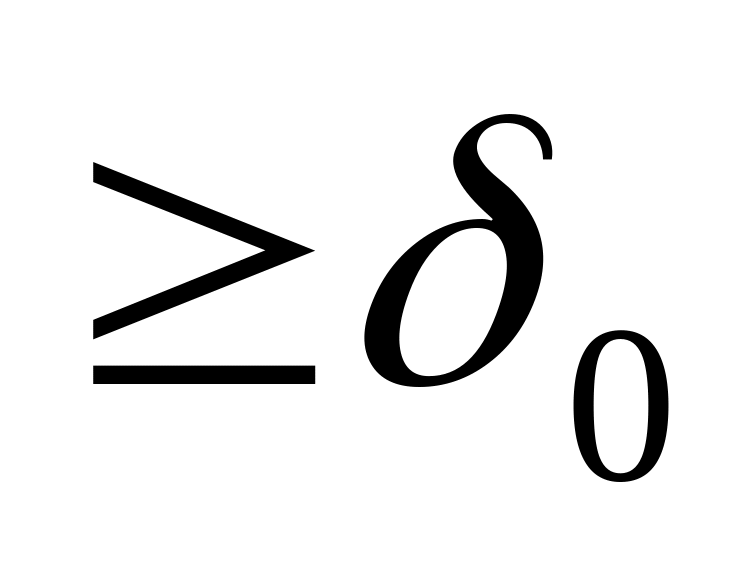 ,
то
,
то
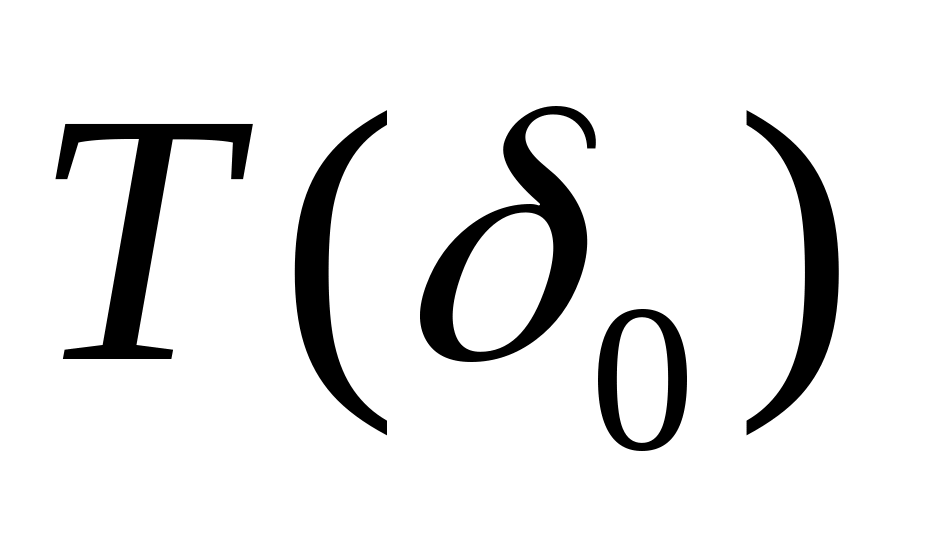 возрастает от 0, когда n=0,
до ограниченной величины //
возрастает от 0, когда n=0,
до ограниченной величины //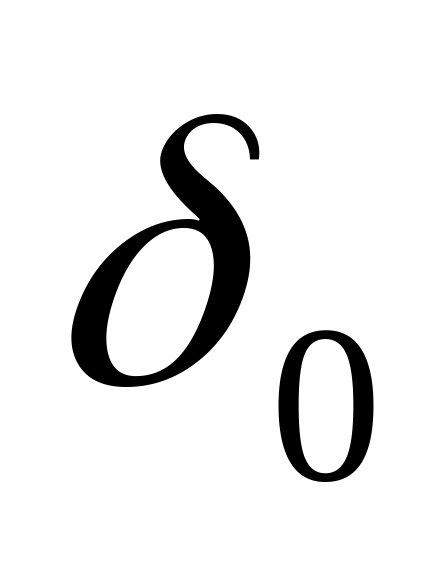 при
.
при
.Если g
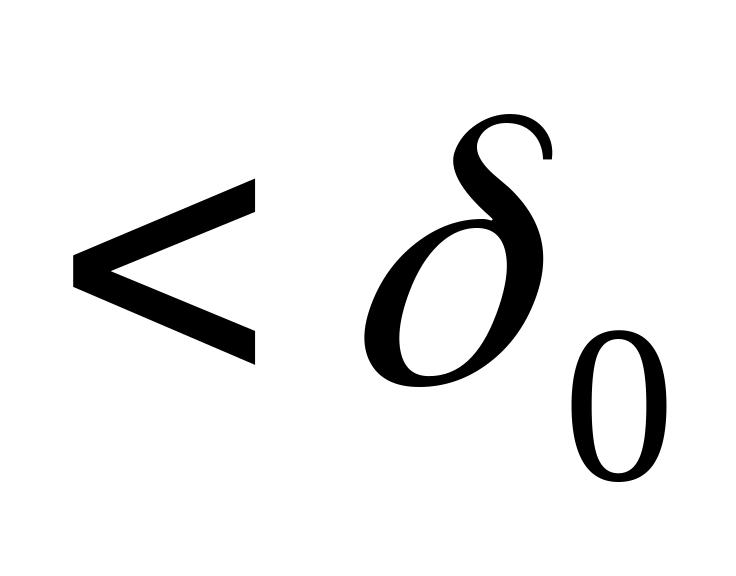 ,
то
возрастает от 0 при n=0, до
такого n, что
,
то
возрастает от 0 при n=0, до
такого n, что
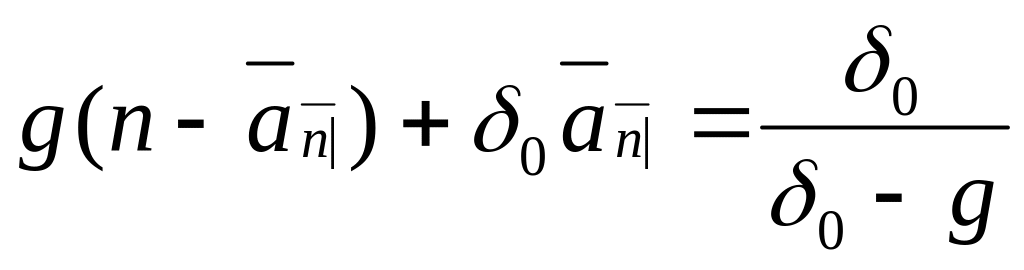 (9).
(9).
После которого уменьшается до //![]() при
(уравнение (9) может быть решено численно)
при
(уравнение (9) может быть решено численно)
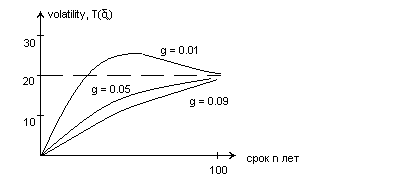
Т.о. возможно, при данной интенсивности
,
что volatility опред. долгосрочных
низкопроц. погашаемых акций превосходит
вечную ренту. Это такие акции для которых
![]() ,
т.е.
,
т.е.
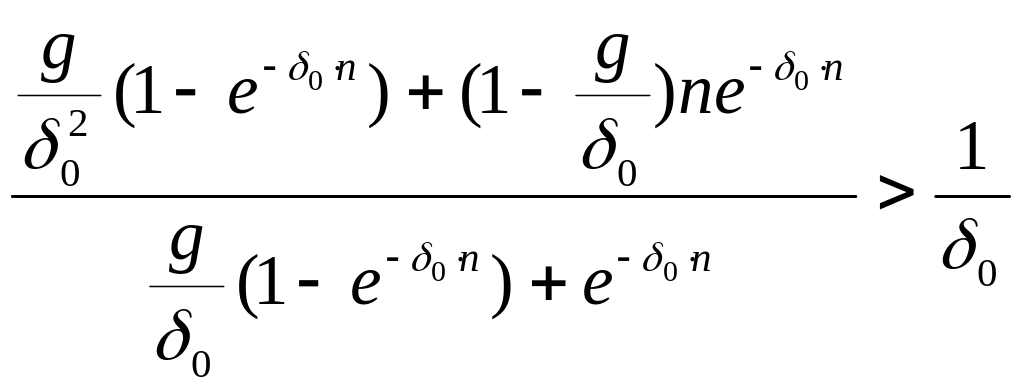
Неравенство выполняется тогда и только тогда
![]() (10)
(10)
n>![]() ;
g<
;
g<![]()
Т.о. если даны g и
и 0<g<![]() погашаемая акция с пропорциональной
ставкой g за единицу долгового обязательства
будет иметь больший volatility
, чем вечная рента . Тогда и только тогда
срок погашения превосходит
погашаемая акция с пропорциональной
ставкой g за единицу долгового обязательства
будет иметь больший volatility
, чем вечная рента . Тогда и только тогда
срок погашения превосходит
![]() Если даны
и n, погашаемая акция со
сроком n будет иметь
больший volatility, чем вечная
рента тогда и только тогда когда
процентная ставка за единицу долгового
обязательства меньше чем
-
Если даны
и n, погашаемая акция со
сроком n будет иметь
больший volatility, чем вечная
рента тогда и только тогда когда
процентная ставка за единицу долгового
обязательства меньше чем
-![]() .
.
Предельная величина при
равна
![]() .
.
Пример10.4.1. Спекулянт покупает большое количество ценных бумаг с фиксированной процентной ставкой, когда он ожидал, что процентные ставки упадут, с целью их продажи в короткий срок для получения прибыли. Сейчас он выбирает между двумя акциями с фиксированным процентом:
Ценная бумага 1. Приносит 5% ежегодно в конце года и погашается по номиналу через 5 лет.
Ценная бумага 2. Приносит 11%ежегодно в конце года и погашается по номиналу через 6 лет.
Эти акции всегда имеют один и тот же валовой доход за год 10%. Какую акцию он должен купить, чтобы получить большую капитальную прибыль на малое падение процентных ставок? (без налогов)
Решение. Величина volatility для каждой ценной бумаги : (по формуле (1))
ЦБ1:
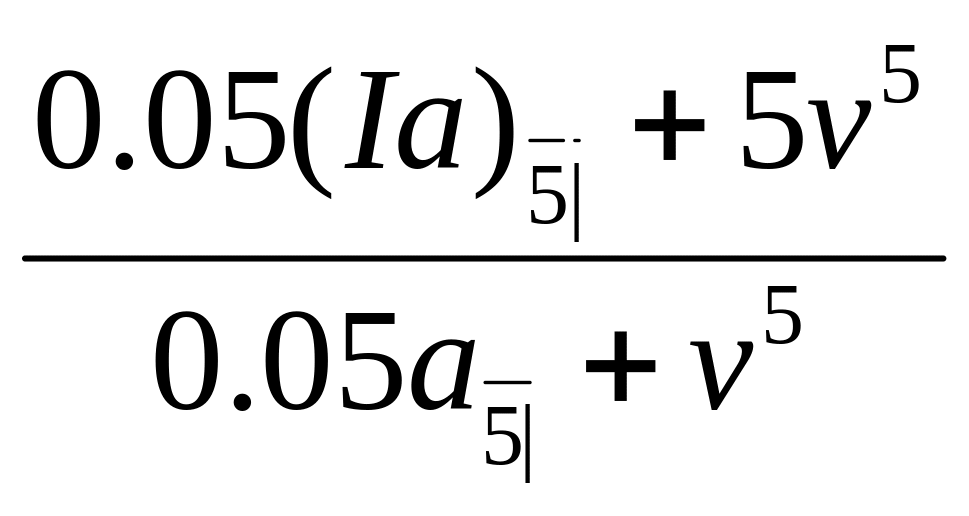 at 10% = 4.488
at 10% = 4.488
ЦБ2:
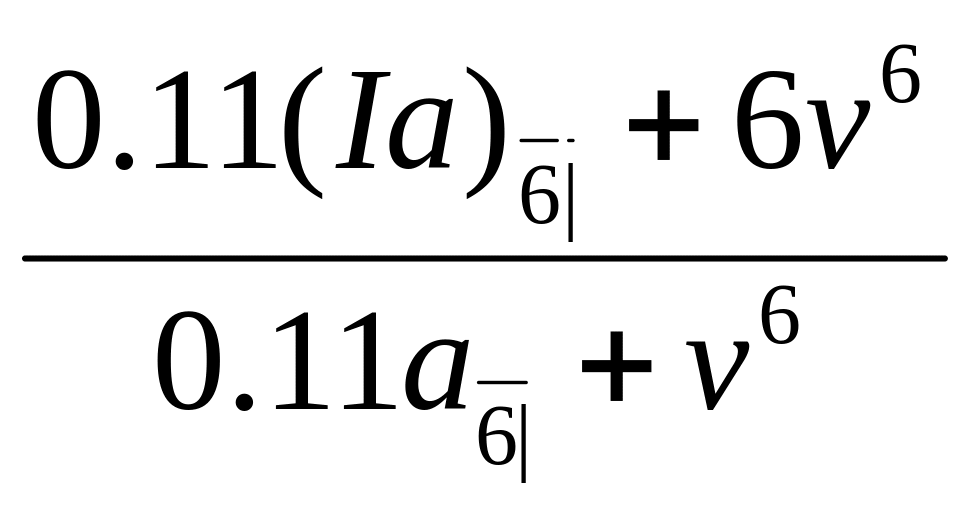 at 10% = 4.725
at 10% = 4.725
Следовательно спекулянт выберет ЦБ2.
Пример10.4.2. Когда δ = 0.08 цены за единичный номинал 2-ух ценных бумаг с фиксированными процентами A и B равны и известно, что когда
0.05
![]() 0.8.
0.8.
volatility A
![]() volatility B.
volatility B.
Доказать, что если интенсивность изменяется непрерывно от 0.008 за год до 0.05, тогда новая цена акции А будет меньше новой цены акции В.
Решение.
Пусть
![]() и
и
![]() - цены единичного номинала А и В.
- цены единичного номинала А и В.
Имеем:
![]()
Из уравнения (3.4):
![]() ,
,
![]()
Отсюда, если мы положим
![]() ,
,
то
![]() (0.08) = 0,
(0.08) = 0,
![]() ,
.
Следовательно, по теореме о среднем
значении
,
.
Следовательно, по теореме о среднем
значении
![]() и
и
![]() т.е.
т.е.
![]()
