3.3. Розрахунок і побудова графіків приросту кінетичної енергії

За умовами завдання визначені: маси, кг: куліси m₃; шатуна m₄; повзуна m₅=m₄; моменти інерції, кг: кривошипа I_o1; куліси ; шатуна . Їх значення надані у табл. 2.

Повна кінетична енергія представляє суму кінетичних енергій:

Т_I – ланок із сталим зведеним моментом інерції I_I і

Т_II – інших ланок зі змінним зведеним моментом інерції I_II.

Відповідної цієї енергії змінний момент інерції .

Кінетична енергія Т_II розраховується за формулі:

, Дж.

Весь цей розрахунок проводиться у формі таблиці 7. Для побудови графіка кінетичної енергії Т_II() у таблиці визначені значення ординат , де _Т=_А відповідає масштабу робіт (див. табл. 6).

Таблиця 7. Результати розрахунків і побудов діаграм кінетичних енергій

Приріст кінетичної енергії Т= Т-Тпоч_.=А_р.-А_о.. Тому, вимірявши відстань між графіками А_дв() і Ас(), побудуємо діаграму Т() у масштабі _Т = _А. Для першої групи ланок з I_I= const перепад кінетичних енергій Т_I^/=Т-Т_II.

Вирахування ординат графіків Т() і Т_II(), побудованих у єдиному масштабі _Т1, дозволяє одержати графік Т_I^/(). Найбільший приріст кінетичної енергії цієї групи ланок на графіку відповідає відрізку CD, мм. Перепад енергій Т_1max=(CD)_Т, Дж. Наведений момент інерції , за допомогою якого забезпечується необхідна нерівномірність обертання , буде дорівнює: .

4. Визначення моменту інерції маховика та його геометричних розмірів

Приведений момент інерції першої групи ланок , де – загадне передаточне відношення передачі від двигуна до важільного механізму; – момент інерції маховика, який установлюється на валу кривошипа важільного механізму, –момент інерції ротора асинхронного двигуна. Таким чином, , кгм²

Задамося відносними розмірами: . Вважаючи масу маховика розподіленою по ободу, можна вивести залежність для розрахунку середнього діаметра обода , де  – щільність матеріалу маховика. прийнявши як матеріал маховика чавун з щільністю =7100кг/м³, розрахуємо: м.

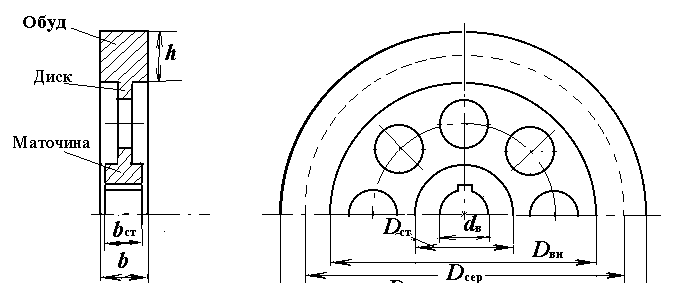
Рис. 8. Ескіз махового колеса

Розміри обуда: В=bD_сер; H=hD_сер; D_нар=D_сер+Н; D_унутр= D_сер – Н. Інші розміри: діаметр вала приймається рівним мм; діаметр маточини приймається =2d_в ; ширина маточини приймається рівній ширині обода =В; товщина полотнини диска В_п  0,25В; середній діаметр отворів D_отв= 0,5(D_внутр + d_ст), мм.

Маса обуда , кг. Масу всього маховика приймаємо: m_мах  1,15m_об., кг.

Результати розрахунків маховика внесемо до табл.8.

Таблиця 8. Розрахунки махового колеса та прискорення кривошипа

4. Розрахунок кутового прискорення кривошипа

Кутове прискорення для заданого положення розраховується за формулою: ,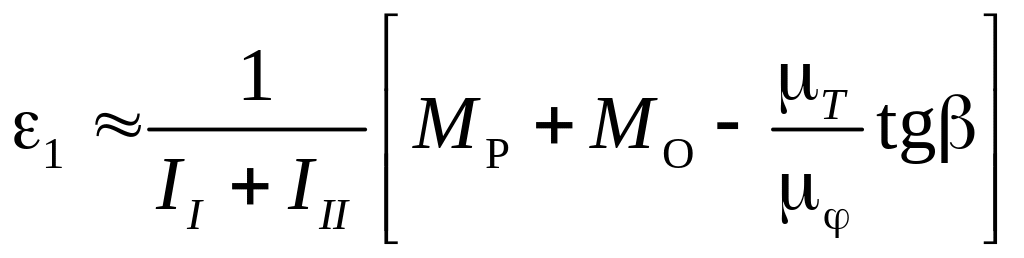

де  – кут нахилу дотичної до графіка залежності Т_II(). Для заданих положень усі розрахунки виконані у табличному вигляді (див. табл. 8).

4. Кiнетостатичне дослідження важільного механізму

4.1. Визначення зовнішніх і інерційних навантажень на ланки механізму.

Розрахунок виконується для заданого положення. Зовнішнє навантаження є силою опору, яка визначається згідно завдання (див. рис. 2). До ланок прикладені сили ваги, що визначаються за відомою залежністю , Н, м/с².

Інерційні навантаження розраховуються відповідно до принципу Даламбера: .

Знак (-) у цих формулах означає, що ці вектора протилежні відповідним прискоренням. Після підстановок і розрахунків одержуємо значення модулів навантажень, яки наведені у табл. 9.