2. Кінематичне дослідження важільного механізму

   1. Розрахунок і побудова планів механізму

Для вибору масштабу побудови планів необхідно визначити максимальні габарити кулісного механізму зубодовбального верстата (рис. 1). З цією метою можна скористатися наступними залежностями:

• по вертикалі Y_max ≤ l_CK·sin 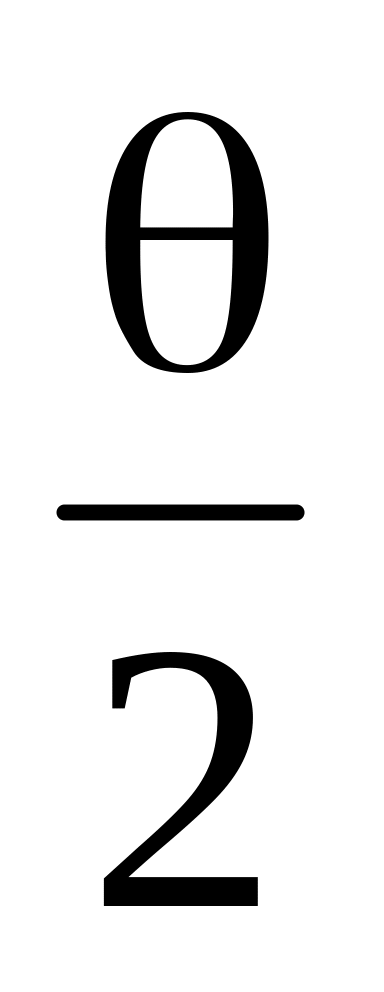+l_CD, м;

• по горизонталі X_max= l_CK + с, м.

Для зображення кінематичної схеми приймаємо масштабний коефіцієнт _l, м/мм. У прийнятому масштабі відповідні відрізки l_i ланок будуть мати розміри , обумовлені формулою . Результати розрахунків надані у табл.1.

Плани механізму й відповідні плани швидкостей будуються для 12 обов'язкових положень кривошипа й 2-х додаткових положень, що відповідають початку й закінченню процесу різання. Результати розрахунків і побудов представлені у табл. 3.

2. Розрахунок і побудова планів швидкостей

Кінематичний розрахунок методом планів починається з розрахунку вхідної ланки, закон руху якого заданий. Кінематичне дослідження виконується за допущенням про сталість кутової швидкості кривошипа, , де , с^-1.

Цей розрахунок можна виконувати в наступній послідовності.

Центр шарніра А належить вхідній ланці – кривошипу 1, каменю 2 і кулісі 3 тому для кожної із цих ланок точка має відповідний номерний індекс: і . Точки розташовані на осі шарніра, що з'єднує кривошип і камінь, друг щодо друга не зміщаються, тому для цих точок всі кінематичні характеристики збігаються в будь-який момент часу. Для цих точок значення швидкості розраховується по формулі , м/с. Вектор швидкості спрямований убік обертання кривошипа (проти годинникової стрілки) перпендикулярно до прямій ОА, тобто . Таким чином, швидкість повністю визначена за величиною й напрямком.

Точка перебуває на кулісі 3, з'єднаної з каменем 2 поступальною парою. Для визначення швидкості точки складається векторне рівняння по теоремі про складний рух точки, . У цьому рівнянні вектор підкреслять подвійною рисою, тому що обидва параметри, його визначальні, були знайдені в попередньому пункті. Швидкість точки розташована на кулісі, яка повертається навколо нерухливого центра В, тому , величина її невідома, у рівнянні вектор підкреслюється одинарною рисою. Теж можна сказати про вектор швидкості ковзання каменю уздовж куліси, тобто . Це векторне рівняння вирішується графічно, оскільки в ньому невідомі тільки модулі векторів і .

Для побудови плану швидкостей необхідно вибрати масштабний коефіцієнт . Його величина підбирається відповідно до вже відомого значення лінійної швидкості такою, щоб величина відрізка перебувала в діапазоні розмірів мм. Побудова плану швидкостей проводиться за векторним рівнянням й починається з вибору місця полюса плану, точки . Від цієї точки в напрямку вектора вычерчивается відрізок , тобто . Через точку , що збігається із точкою , проводиться лінія, паралельна осі куліси АВ. З полюса проводиться лінія, перпендикулярна до осі куліси. Перетинання цих прямих визначає точку , що є одночасно кінцем вектора і початком вектора відносної швидкості . Для побудови вектора швидкості точки варто скористатися теоремою подоби, відповідно до якої складена пропорція: . Величина відрізка , що входить у цю пропорцію, заміриться на плані механізму. Із пропорції розраховується величина відрізка й відкладається на продовженні вектора у протилежному від полюса напрямку. За теоремою уподобання , , м/с.

Після побудови плану швидкостей заміряться відрізки, що зображують лінійні швидкості й розраховуються дійсні значення цих швидкостей: , м/с; , м/с; , м/с.

Кутова швидкість куліси3 розраховується за формулою , з^-1. У цій формулі , м. Напрямок кутової швидкості куліси можна визначити, якщо помістити в точку А плану механізму вектор і спостерігати за ним із точки В.

Швидкість точки D перебуває по теоремі про плоскопаралельний рух твердого тіла (шатуна) . Тут вектор визначений за величиною й напрямком ( ), а швидкості: , . За результатами побудови цієї частини плану швидкостей розраховуються лінійні швидкості точок: ; ; . Точка S₄ ділить відрізок cd навпіл. Кутова швидкість шатуна 4: . Результати розрахунків і побудов заносяться в табл. 3.