Скольжение профилей. Коэффициенты удельных скольжений

В следствиях из основной теоремы зацепления установлено, что в процессе зацепления происходит проскальзывание контактирующих профилей из-за того, что проекции скоростей точек контакта профилей на общую касательную к профилям в точке контакта не одинаковы. Скольжение профилей – явление нежелательное, поскольку оно вызывает:

1) потери мощности на трение;

2) износ рабочих контактирующих поверхностей.

В связи с этим оценка скольжения профилей является также одной из основных качественных показателей зацепления.

Рассмотрим процесс скольжения двух профилей произвольной формы. Пусть эти два профиля в настоящий момент времени контактируют в точке А (рис. 3).

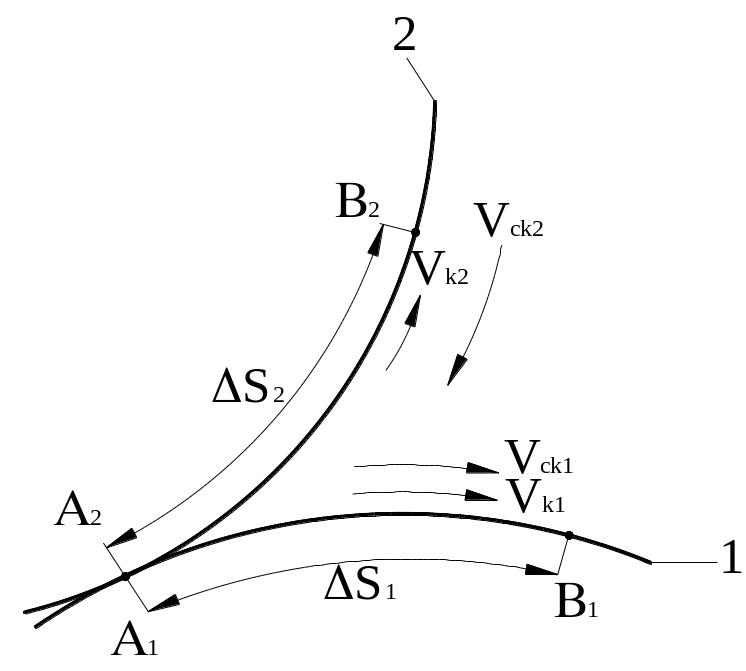
Рисунок 3 – Скольжение профилей. Коэффициенты удельных скольжений

Через некоторое время t точка контакта переместится по первому профилю на расстояние S₁, а по второму – S₂ (A₁B₁=S₁, A₂B₂=S₂).

Если пути, пройденные точкой контакта по обоим профилям одинаковы S₁ = S₂, то скольжение профилей отсутствует. В этом случае профили перекатываются друг по другу без скольжения.

Если пути, пройденные точкой контакта за одно и то же время t не одинаковы S₁  S₂, то существует скольжение профилей друг по другу.

Предположим, что перемещение точки контакта по первому профилю больше чем по второму S₁ > S₂.

Тогда S₁–S₂ есть величина проскальзывания точки контакта по первому профилю, a S₂–S₁ – величина проскальзывания точки контакта по второму профилю. Величина скольжения по первому профилю (S₁–S₂) – положительная, а по второму (S₂–S₁) – отрицательная величина. По модулю величины проскальзывания по первому и второму профилю одинаковые:

S₁–S₂=S₂–S₁.

Обозначим скорость перемещения точки контакта по первому профилю V_k1, по второму – V_k2, а скорости скольжения соответственно V_сk1 и V_сk2. Скорости перемещения совпадают с направлением перемещения точки контакта.

Скорости скольжения V_сk1 и V_сk2 будут совпадать с направлением скольжения профилей.

Поскольку S₁–S₂ – величина положительная, то направление скорости скольжения V_ck1 совпадает с направлением перемещения точки контакта V_k1.

Величина проскальзывания точки контакта по второму профилю S₂–S₁ отрицательна, поэтому и направление скорости скольжения V_ck2 не совпадает со скоростью перемещения точки контакта V_k2.

Определим скорость скольжения точки контакта по первому профилю. Средняя скорость скольжения по первому профилю есть путь скольжения точки контакта по первому профилю, деленный на время скольжения – время перемещения точки контакта:

.

Мгновенное значение скорости скольжения точки контакта по первому профилю определим как предел, к которому стремится средняя скорость при времени скольжения стремящемуся к нулю:

В полученном выражении: – есть скорость перемещения точки контакта по первому профилю, – скорость перемещения точки контакта по второму профилю.

Таким образом скорость скольжения точки контакта по первому профилю равна разности скоростей перемещения точки контакта по первому и второму профилям:

V_ck1= V_k1–V_k2 .

Аналогично получим скорость скольжения точки контакта по второму профилю:

V_ck2= V_k2–V_k1 .

В нашем случае скорость скольжения V_ck1 по первому профилю величина положительная – совпадает с направлением перемещения точки контакта, V_ck2 –отрицательная величина – направлена в сторону противоположную перемещению точки контакта.