О множествах

Понятие (слово) «множество» до второй половины XIX века не имел узко математическое применение, а применялось лишь в общем смысле (множество рабочих на фабрике, множество банков в стране, множество книг в библиотеке и т.п.). Благодаря прежде всего трудам немецкого математика Георг Кантора (1845-1918) (а также Р. Дедекинда, К. Вейерштрасса, Джорджа Буля и др.) термин «множество» приобрел и узко математический смысл.

«Множество» один из основных математических структур, ключевое понятие в теории множеств и логики, математической логики и дискретной математики. Это понятие имеет определения с разных точек зрения, но одинаковые по смыслу. Например, следующие определения:

- Множеством называют всякую совокупность каких-либо предметов (символов, понятий), объединенных каким-то общим признаком.

- Множество – это совокупность вполне определенных и различимых (между собой) объектов любой природы, представляемых как единое целое.

Эти предметы (символы, объекты) называются элементами множества. Например, множество натуральных чисел N, множество всех психологов города, множество студентов данного университета и т.п.

Если все элементы некого множества В принадлежат также множеству А, то можно говорить, что множество В является подмножеством множества А и это символически пишу в виде: 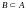. Пустое множество (не содержащее ни одного элемента) обозначают символом . Формально пустое множество можно считать подмножеством любого множества. Множество может быть замкнутым и незамкнутым, полным и пустым, упорядоченным и неупорядоченным, счётным и несчётным, конечным и бесконечным. Множество считается заданным, если известны его элементы.

Множество можно задавать двояко: либо перечислением его элементов (которые записываются в фигурных скобках), либо задают специальное правило, по которому можно четко определить относится рассматриваемый элемент к множеству (соблюдено правило) или нет.

Примеры записи множеств первым способом:

А = {а, б, в} – множество трех начальных букв;

С = {0, 1, 2, 3, …, 9} – множество цифр десятичной системы счисления;

Примеры записи множеств вторым способом:

Х = {х| 1< x < 10} – множество значений х из интервала (1, 10);

Y = {y| P(y)} – означает, что Y множество всех таких элементов y, для которых высказывание (выражение) P(y) истинно.

О том, что «элемент х принадлежит множеству Х» математически пишут так: 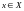, где символ « » называют квантором принадлежности. Если элемент х не принадлежит множеству Х, то пишут 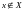. Пусть задано числовое множество X = {x| x<1 и x>3}. Это множество не содержит никаких элементов, так как одновременно и меньше единицы и больше трех невозможно. Множество, не содержащее никаких элементов, называют пустым и обозначают 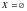. Множество Х = {0} непустое, так как содержит один элемент «0».

Элементы множества могут быть записаны в любом порядке, например, {1, 2, 3} или {3, 1, 2} – одно и то же множество.

Определения:

2. Два множества А и В равны, если состоят из одних и тех же элементов. Пишут А = В.

3. Если между элементами А и В можно установить взаимно однозначное соответствие по любому закону, то эти множества называются эквивалентными, или равномощными: .

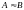Установление взаимно однозначного соответствия между элементами множеств пригодно для сравнения и бесконечных множеств (имеющих бесконечное количество элементов). Например, множество N (всех натуральных чисел) эквивалентно множеству всех четных чисел, так как каждому числу n соответствует одно и только одно четное число 2n, и наоборот, каждому четному числу 2n соответствует его половина n, являющаяся натуральным числом. Т.е. есть взаимно однозначное соответствие.

4. Счетным называется всякое множество, элементы которого можно пронумеровать (т.е. поставить во взаимно однозначное соответствие со всеми числами натурального ряда).

Иначе говоря, множество А называется счетным, если оно эквивалентно множеству натуральных чисел N.

5. Бесконечные множества называются множествами равной мощности, если эквивалентны меду собой.

Для конечных множеств мощностью называется число их элементов.

Все эквивалентные бесконечные множества имеют одинаковую мощность, это то общее, что их объединяет. О множествах, эквивалентных множеству всех действительных чисел, принадлежащих отрезку [0,1], говорят, что они имеют мощность континуума (от латинского continuum – непрерывность).

6. Семейством множеств называется множество, элементы которого сами являются множествами.

7. Если каждый элемент множества А является также элементом множества В, то А называется подмножеством В, т.е. А содержится в В (или включено в множество В) и об этом пишут: 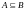(можно сравнивать с символом ).

Если все элементы А являются также элементами В, но кроме них В имеет еще и другие элементы, то А называется собственным подмножеством В и записывается так: .

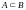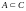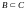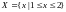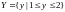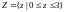Например, пусть даны множества: A={a,b,c}, B={a,b,c}, C={a,b,c,d,e}, тогда по определениям имеем , , . Или же другой пример: , , , тогда 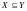(также ), , .

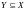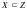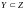Основные свойства включения: 1) 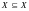; 2) если , а 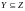, то следует 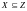; 3) и , то .

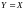8. Каждое непустое множество 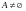имеет по крайней мере два различных подмножества: это само множество А и пустое множество . Более того, каждый элемент А может считаться подмножеством А (например, если 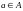, то ).

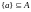9. Множеством-степенью множества А называется семейство всех подмножеств А и обозначается P(A).

Например, А ={0,1,2}, то P(A)={A, , {0},{1},{2}, {0,1},{0,2}, {1,2}}.

10. Множество называется конечным, если количество его элементов может быть выражено некоторым положительным числом. Причем неважно, известно это число или нет, а важен лишь факт существования такого числа.

Например, множество цифр в десятичной системе, множество букв латинского алфавита, множество квартир конкретного микрорайона, множество студентов данного вуза и т.д.

Если конечное множество A содержит n элементов, то его множество-степень P(A) содержит 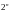элементов.

Бесконечные множества являются объектами математики. Например, бесконечное множество натуральных чисел, целых, рациональных, действительных и комплексных чисел. Бесконечно также множество всех точек данного отрезка, прямой, плоскости или множество всех прямых проходящих через одну данную точку и т.д.

Операции над множествами. Алгебра множеств.

Определения:

11. Объединением множеств А и В называется множество 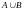, все элементы которого принадлежат хотя бы оного из них (т.е. или А или В или обеим одновременно). Пишут .

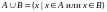12. Пересечением множеств А и В называется множество 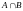, все элементы которого принадлежат обоих множеств А и В. Пишут .

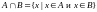Из определения следует, что 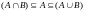и .

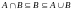13. Относительным дополнением множества А до множества Х (или говорят разностью множества Х и А) называется множество Х/A всех тех элементов Х, которые не принадлежат множеству А: .

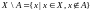14. Симметрической разностью множества А и В называется множество:

.

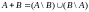15. Универсальное множество U. Если все рассматриваемые в ходе данного рассуждения множества являются подмножествами некоторого множества U, то U называется универсальным множеством для данного рассуждения.

16. Абсолютным дополнением множества А называют множество всех тех элементов х, которые не принадлежат А и обозначают символом ͞А . ͞A = U\A. Ясно, что Х\A = X∩͞A.

Основные тождества алгебры множеств

1). А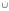 В = В А (коммутативность операции объединения ), а также А∩В = В∩А.

2). А (В С) = (А В) С (ассоциативность ), а также А∩(В∩С) = (А∩В) ∩С.

3). А (В∩С) = (А В) ∩(А С) (дистрибутивность относительно ∩), а также

А∩(В С) = (А∩В) (А∩С).

4). 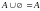; а также А∩U = А. 5). 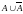= U; А∩͞А= .

6). 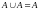; 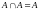. 7). А U= U, .

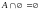8). 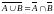, а также 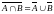(закон де Моргана).

9). 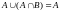; 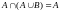(закон поглощения).

Прямое (декартовое) произведение множеств

Понятия упорядоченной пары и упорядоченной n-ки элементов являются исходными (как и понятие множества). В бинарных отношениях участвуют пары элементов множеств, так называемые упорядоченные пары <x,y> - означает, что строго на первом месте всегда стоят элементы одного множества , а на втором 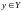. Упорядоченная n-ка элементов х₁, х₂,…,х_n обозначается < х₁, х₂,…,х_n > и, по определению, можно выразить так: << х₁, х₂,…,х_n-1>, x_n>. Элементы х₁, х₂,…,х_n называются компонентами или координатами n-ки (также называют кортежем элементов).

Прямым (декартовым) произведением множеств X и Y называется множество всех упорядоченных пар <x,y> , таких, что и ; обозначается через .

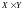Пример 2.

1. Даны множества: Х = {1,2,3}, Y = {0,1}. Тогда прямое произведение

= {<1,0>, <1,1>, <2,0>, <2,1>, <3,0>, <3,1>};

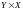= {<0,1>, <0,2>, <0,3>, <1,1>, <1,2>, <1,3>}.

Кроме прямого произведения, мы еще замечаем, что

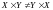
2. Пусть Х множество точек отрезка [0,1], а Y – отрезка [1,2]. Тогда прямое произведение даст множество точек квадрата с вершинами (0,1), (0,2), (1,1), (1,2).