Лабораторная работа №15. Градиентные методы решения задач оптимизации

Цель работы:

• определить координаты точки экстремума целевой функций с использованием метода градиента и наискорейшего спуска;

• доказать, что найденный экстремум является глобальным;

• сопоставить эффективность использованных методов.

1. ОПИСАНИЕ МЕТОДИКИ РАСЧЕТОВ

Среди методов, применяемых для решения задач оптимизации методами нелинейного программирования, значительное место занимают методы поиска решения, основанные на анализе производных оптимизируемой функции.

Предполагается в дальнейшем, что анализируются только непрерывные дифференцируемые функции R(U).

Рис. 15.1

В градиентных методах используется следующее свойство градиента целевой функции: вектор градиента по направлению совпадает с направлением наискорейшего возрастания целевой функции. Поэтому движение к точке экстремума производится по направлению градиента целевой функции (при поиске максимума), а в случае поиска минимума – в противоположном направлении. Направление градиента перпендикулярно в любой точке линии постоянного уровня, поскольку вдоль этой линии функция постоянна (см. рис. 15.1).

1.1. Метод градиента

Поиск экстремума при использовании метода градиента осуществляется в два этапа. На первом находятся значения частных производных по всем независимым переменным, и определяется направление градиента в рассматриваемой точке. На втором этапе осуществляется шаг в выбранном направлении.

Для определения направления градиента необходимо найти значения частных производных по независимым переменным. Если известен аналитический вид целевой функции R(U) и он достаточно прост, то вычисления производных чаще всего не составляет особого труда. В противном случае для нахождения производных используется численный метод, при котором для вычисления производный проводится вспомогательная серия расчетов.

Ниже рассмотрен случай, когда целевая функция зависит от двух независимых переменных (рис. 15.2).

Рис. 15.2

Около выбранной точки К с координатами ( , ) ставятся две вспомогательные точки: – на расстоянии е₁ вдоль оси x₁ и – на расстоянии е₂ вдоль оси x₂. Здесь е₁ и е₂ – достаточно малые приращения независимых переменных. В этих точках с координатами ( +е₁, ) и с координатами ( , +е₂) рассчитываются значения целевой функции. Так же рассчитывается значения целевой функции в исходной точке К.

Частные производные целевой функции пo независимым переменным находятся по следующим формулам:

(15.1)

(15.2)

В данной работе величина шага определяется следующим образом:

, (15.3)

где h – шаг поиска.

Величина приращения независимой переменной при постоянном значении h изменяется автоматически в соответствии с изменением абсолютной величины градиента, что является достоинством данного алгоритма.

Координаты (K+1)-ой точки определяются следующим образом:

. (15.4)

В (15.4) при поиске максимума целевой функции ставиться знак «+», а при поиске минимума – знак «–».

Во вновь найденной (K+1)-ой точке рассчитывается значение целевой функции. В случае удачного шага находиться новое значение градиента и делают новый шаг и т.д. В случае неудачного шага в точке К снова определяют значение градиента, например, при изменённых значениях h либо е.

Поиск продолжают до тех пор, пока не будет определена точка экстремума с заданной точностью. Критерием окончания поиска оптимума является достижение такой точки, при движении из которой по любому направлению дальнейшего убывания функции не происходит. На практике, в качестве признака оптимума часто применяется условие:

Блок-схема метода градиента приведена на рис. 15.3.

1.2 Метол наискорейшего спуска

Метод наискорейшего спуска, объединяющий основные идеи методов релаксации и градиента, заключается в следующем. В исходной точке определяется градиент оптимизируемой функции и тем самым направление ее наискорейшего убывания. Затем вдоль этого направления делается не один шаг, как в методе градиента, а продолжается движение до нахождения частного экстремума вдоль этого направления.

Рис. 15.3. Блок-схема метода градиента

Затем в точке экстремума вновь определяют градиент, и осуществляется движение в новом выбранном направлении до частного экстремума и т.д. до тех пор пока не будет найден абсолютный экстремум.

Сравнение методов градиента, релаксации, наискорейшего спуска позволяет заметить, что в методе наискорейшего спуска сочетаются достоинства методов градиента и релаксации. Метод наискорейшего спуска позволяет найти экстремум при минимальном объёме вычислений. Метод особенно выгодно использовать в том случае, когда градиент функции изменяется не резко. Очевидно, что вблизи экстремума метод наискорейшего спуска вырождается в метод градиента, в качестве критерия окончания поиска можно использовать те же критерии, что и в методе градиента.

Блок-схема метода наискорейшего спуска приведена на рис.15.4.

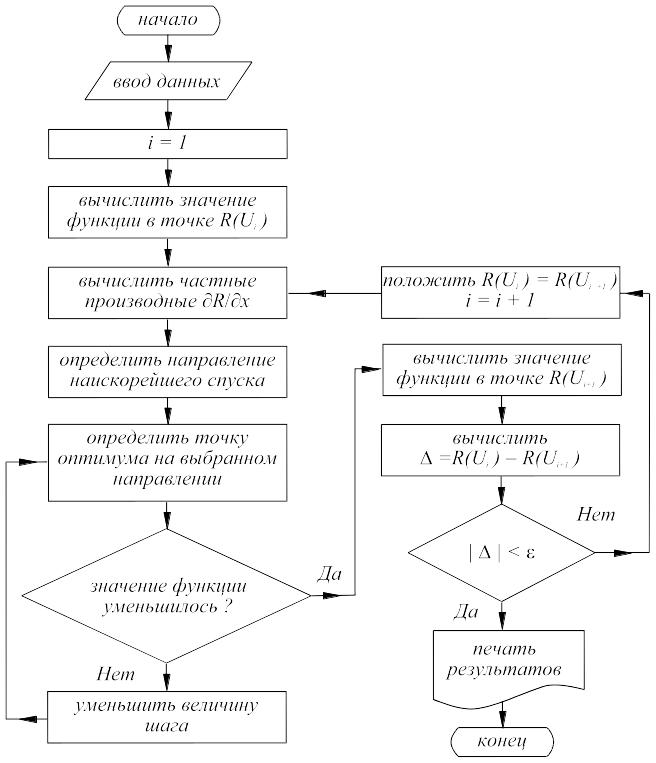
Рис. 15.4. Блок-схема метода наискорейшего спуска

2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Работа выполняется в такой последовательности:

• в директории LABS находят программу «optimize.exe. Градиентные методы» (см. лабораторную работу №13) и выполняют с ее помощью расчеты на ЭВМ согласно своего индивидуального задания, в результате которых определяют координаты точки экстремума целевой функции;

• осуществляют проверку: является ли найденный экстремум глобальным, для чего расчеты повторяются несколько раз из начальных точек с различными координатами.

Ввод исходных данных в программе организован в диалоговом режиме. В качестве исходных данных задаются: вид целевой функции, координаты начальной точки, начальный шаг, величина приращения.

3. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

Вид целевой функции и область допустимых изменений независимых переменных выбирается в соответствии с вариантом задания к лабораторной работе №13 (см. таблицу 13.1). Требуемая точность определения координат точки экстремума 0,001.

4. ОФОРМЛЕНИЕ ПРОТОКОЛА

В протоколе по лабораторной работе описываются результаты расчётов, выполненных на ЭВМ, приводятся блок-схемы методов и доказательства нахождение глобального экстремума.

5. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Классификация методов решения задач оптимизации.

2. Общая идея методов нелинейного программирования.

3. Метод градиента, алгоритм расчета и блок-схема метода градиента.

4. Метод наискорейшего спуска, алгоритм расчета и блок-схема метода, область наивысшей эффективности метода.

5. В чем состоят основные отличия методов градиента и наискорейшего спуска? Каковы условия окончания поиска в этих методах?

6. Методы поиска экстремума функции одной переменной.

7. Доказать, что найденный экстремум является глобальным.