1.2. Метод Хука-Дживса

Данный метод поиска точки экстремума целевой функции является более эффективным по сравнению с методом покоординатного спуска. Поиск состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которым в случае успеха следует поиск по образцу.

Алгоритм метода следующий.

А. Выбирается начальная базисная точка b₁ и шаг h_j для каждой переменной x_j, j=1, 2, ..., n. Можно использовать и одинаковый шаг h для всех переменных, однако указанная выше модификация может оказаться полезной.

Б. Исследующий поиск проводится с целью получения сведений о локальном поведении целевой функции в окрестности базисной точки. Эти сведения в дальнейшем будут использованы для нахождения направления поиска по образцу, с помощью которого можно надеяться достичь большего убывания значения функции.

1. Вычисляется значение целевой функции R(b₁) в базисной точке (b₁).

2. Каждую независимую переменную по очереди изменяем на величину шага. Таким образом, вычисляется значение целевой функции R(b₁+h₁e₁), где e₁ – единичный вектор в направлении оси x₁. Если это приводит к уменьшению значения целевой функции в случае поиска минимума, то b₁ изменяют на b₁+h₁e₁. В противном случае вычисляется значение функции R(b₁–h₁e₁), и если ее значение уменьшилось, то b₁ заменяют b₁–h₁e₁. Если ни один из проделанных шагов не приводит к уменьшению значения целевой функции, то точка b₁ остается неизменной и рассматриваются изменения в направлении оси х₂, т.е. находят значение функции R(b₁+h₂e₁) и т.д. Когда будут рассмотрены все n переменные, то получим новую базисную точку b₂.

3. Если b₂=b₁, т.е. уменьшение функции не было достигнуто, то исследование повторяется вокруг той же базисной точки b₁, но с уменьшенной величиной шага. На практике удовлетворительным считается уменьшение величины шага (шагов) в десять раз от начальной длины.

4. Если b₂b₁, то производится поиск по образцу.

B. При поиске по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом. Эта процедура выполняется таким образом:

1. Разумно двигаться из базисной точки b₂ в направлении b₂–b₁, поскольку поиск в этом направлении уже привел к уменьшению значения целевой функции. Точка образца может быть вычислена следующим образом:

P₁ = b₁ + 2 (b₂ – b₁) (13.5)

В общем случае:

P_i = b_i + 2 (b_i+1 – b_i) (13.6)

2. Проводится исследование в окрестностях точки P₁ (P_i).

3. Если наименьшее значение на шаге B, 2 меньше значения в базисной точке b₂ (в общем случае b_i+1), то получают новую базисную точку b₃ (b_i+2), после чего следует повторить шаг B, 1. В противном случае не производится поиск по образцу из точки b₂ (b_i+1), а заменяется базисная точка. В качестве новой базисной точки выбирается та точка, в которой на предыдущем шаге значение целевой функции было минимальным. Затем выполняется исследование вокруг новой базисной точки.

4. Процесс поиска завершается, когда длина шага (длины шагов) станут меньше заданного малого значения.

Ниже приведена блок-схема данного метода (рис. 13.2), блок-схема этапа 3 приведена на рис. 13.3.

2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Работа выполняется в такой последовательности:

• в директории LABS находят программу «optimize.exe. Безградиентные методы» и выполняют с ее помощью расчеты на ЭВМ согласно своих индивидуальных заданий, в результате которых определяют координаты точки экстремума целевой функции;

• осуществляют проверку – является ли найденный экстремум глобальным, для чего расчеты повторяются несколько раз из начальных точек с различными координатами.

Ввод исходных данных в программе организован в диалоговом режиме. В качестве исходных данных вводятся вид целевой функции, координаты начальной точки, начальный шаг, величина приращения.

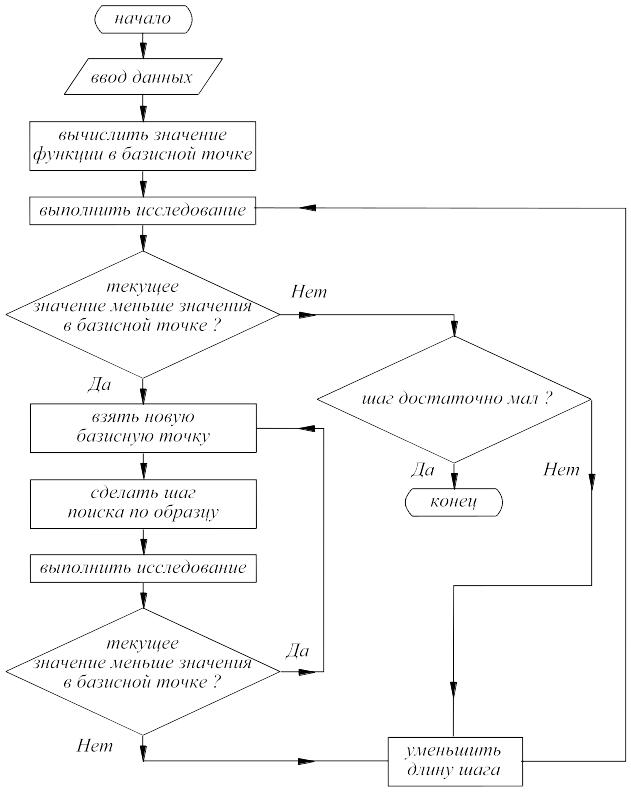
Рис. 13.2. Блок схема метода Хука-Дживса

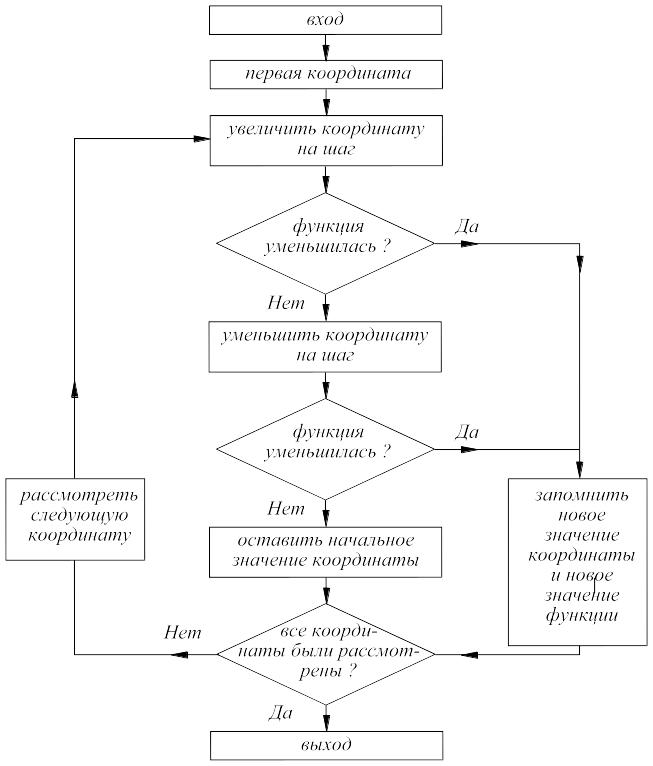
Рис. 13.3. Блок-схема этапа «Выполнить исследование»

3. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

В табл. 13.1. приведены целевые функции и область допустимых изменений исследуемых независимых переменных. Требуемая точность определения координат точки экстремума 0,001.

Таблица 13.1

№ варианта	Целевая функция R=R(x)	Диапазон изменения переменных
1	(x1–1)2+(x2–3)4+4(x3+5)2	–10; +10
2	3(x1–1)4+2(x2–2)2+(x3–3)6	–10; +10
3	3(x1–4)2+5(x2+3) 2+2,5(2x3+5)2	–10; +10
4	(x1–7)4+4(x2–9)2+3(x3–1)4	–10; +10
5	3(2x1+1)4+5(x2+3)2+4(x3–4)2	–10; +10
6	0,5(8x1–32)4+16(3x2+0,9)2+4(5x3–1)2	–10; +10
7	2,5(2x1–1)2+4,8(x2+5)2+1,4(x3–2)2	–10; +10
8	1,5(10x1+2)2+8(6x2–12) 2+3(12x3+6)2	–10; +10
9	12(2x1–2,8)4+3(0,5x2+4)2+14(2,5x3–10)4	–10; +10
10	2(x1–6)4+4(x2+5)2+2(x3–3)4	–10; +10
11	(4x1–2)2+2,5(3x2+4,2)2+(4x3–1,6)2	–10; +10
12	2(x1–3)4+3(x2–1)4+(x3–2)4	–10; +10
13	10(3x1–18)2+2(12x2+18)2+11(5x3–10)2	–10; +10
14	3(x1–5)4+5(x2+1)2+4(x3–4)4	–10; +10
15	(4x1–1)2+4,5(2x2+3,2)2+(5x3–1,5)2	–10; +10
16	(x1–7)2+(x2–2)4+5(x3+4)2	–10; +10
17	4(x1–4)4+4(x2–6)4+(x3–1)6	–10; +10
18	2(x1–2)2+2(x2+1)2+1,5(2x3–6)2	–10; +10
19	(x1–5)4+5(x2–7)2+3(x3–2)4	–10; +10
20	4(2x1+3)4+3(x2+2)2+2(x3–5)2	–10; +10

4. ОФОРМЛЕНИЕ ПРОТОКОЛА

В протоколе по лабораторной работе описываются результаты расчетов, выполненных на ЭВМ, приводятся доказательства нахождения глобального экстремума.

5. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Классификация методов решения задач оптимизации.

2. Общая идея методов нелинейного программирования.

3. Метод покоординатного спуска, алгоритм расчета.

4. Составить блок-схему метода покоординатного спуска.

5. Метод Хука-Дживса, алгоритм расчета.

6. Общая блок-схема метода Хука-Дживса.

7. Блок-схема поиска в базисной точке.

8. Как доказать, что найденный экстремум является глобальным?

9. Основные достоинства и недостатки методов покоординатного спуска и Хука-Дживса.

10. Может ли в методе покоординатного спуска оказывать влияние на результат (значение оптимума) и на эффективность поиска порядок чередования переменных.