Лабораторная работа №14. Симплексные методы решения задач оптимизации

Цель работы:

• составить подпрограмму для расчета целевой функции;

• определить точки экстремума целевой функции с использованием прикладных программ, реализующих симплексный метод и метод Нелдера-Мида;

• сопоставить эффективность используемых методов.

1. ОПИСАНИЕ МЕТОДИКИ РАСЧЕТОВ

1.1. Симплексный метод

Основная идея этого метода заключается в том, что по известным значениям целевой функции в вершинах выпуклого многогранника называемого симплексом, находится направление, в котором требуется сделать следующий шаг, чтобы получить наибольшее уменьшение (увеличение) значения целевой функции. При этом под симплексом в n-мерном пространстве понимается выпуклый многогранник, имеющий n+1 вершину. Примером симплекса в двухмерном пространстве, т.е. на плоскости, является треугольник. В трехмерном пространстве – тетраэдр.

Симплекс обладает следующим свойством: против любой из его вершин S_j расположена только одна грань, на которой можно построить новый симплекс, отличающийся от прежнего расположением новой вершины , тогда как остальные вершины обоих симплексов совпадают. Вершина нового симплекса , вообще говоря, может находиться и по другую сторону грани от вершины S_j. Это свойство симплекса и обусловило возможность его применения при решении задач оптимизации.

1.2. Алгоритм симплексного метода

Пусть вершинам исходного симплекса S_i (i=1,2,...,n+1) отвечают координаты U⁽ⁱ⁾=(U₁⁽ⁱ⁾,U₂⁽ⁱ⁾,...,U_n⁽ⁱ⁾), (i=1,2,...,n+1). Наибольшее значение целевой функции соответствует вершине S_j. Определим координаты вершины нового симплекса.

Вершина располагается симметрично вершине S_j относительно середины грани, находящейся против вершины S_j. Координаты центра этой грани U^(A) определяются по формуле:

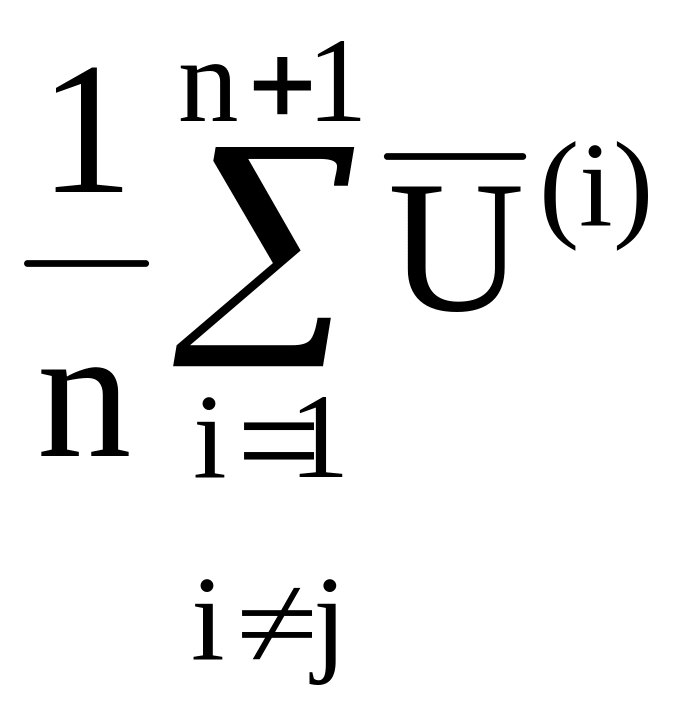= , (14.1)

причем суммирование ведется только по тем векторам , которые отвечают вершинам S_i, образующим эту грань.

Вектор , характеризующий расстояние от вершины S_j до центра противолежащей грани, будет равен:

. (14.2)

Координаты вершины определяются по формуле

. (14.3)

Подставив в выражение (14.3) для U^(A) из (14.1), получим:

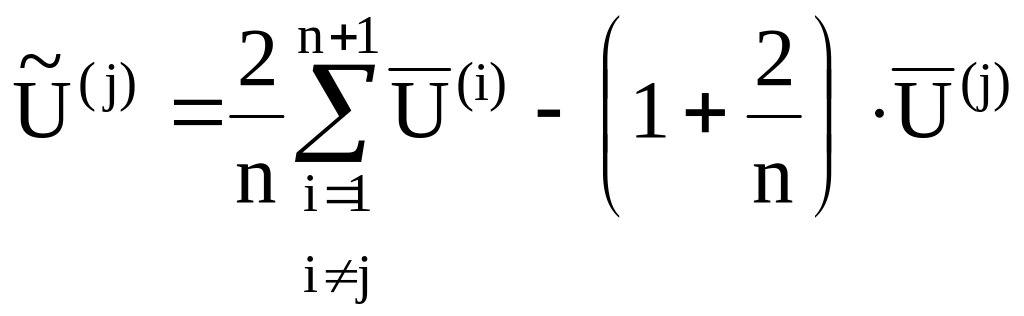. (14.4)

Формула (14.4) определяет координаты вершины нового симплекса.

При необходимости уменьшить размеры симплекса (в случае зацикливания в окрестности точки оптимума) вместо формулы (14.2) можно пользоваться следующим выражением:

(14.5)

Наиболее эффективно симплексный метод сходится при использовании правильных симплексов – равностороннего треугольника или тетраэдра, образованного равносторонними треугольниками. В этом случае направление поиска совпадает с направлением градиента (если симплекс достаточно мал).

Симплексный метод обладает еще одним важным достоинством – при увеличении размерности задачи вычислительные затраты возрастают незначительно, т.к. на каждом шаге считается только одно значение целевой функции. Блок-схема метода приведена на рис. 14.1.

1.3. Метод Нелдера-Мида

В данном методе симплекс перемещается с помощью трех операций: отражения, растяжения и сжатия. Смысл этих операций станет понятным при рассмотрении шагов процедуры.

А. Найдем значения функции в вершинах симплекса.

f ₁= f(х₁); f₂=f(х₂);.....f_n+1=f(х_n+1)

Б. Найдем наибольшее значение функции f_h, следующее за наибольшим значением функции f_g, наименьшее значение функции f_l и соответствующие им точки x_h, x_g, и x_l.

В. Найдем центр тяжести всех точек, за исключением точки x_h.

х₀ =

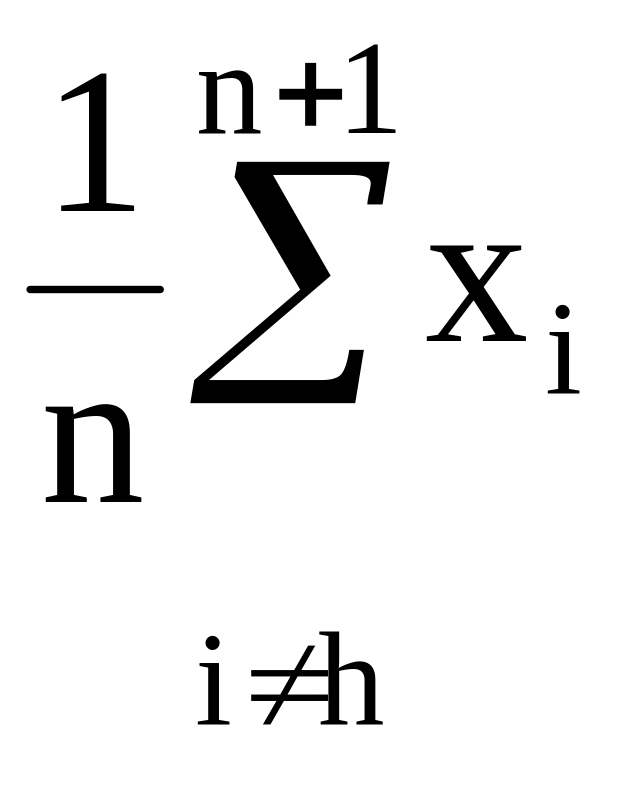
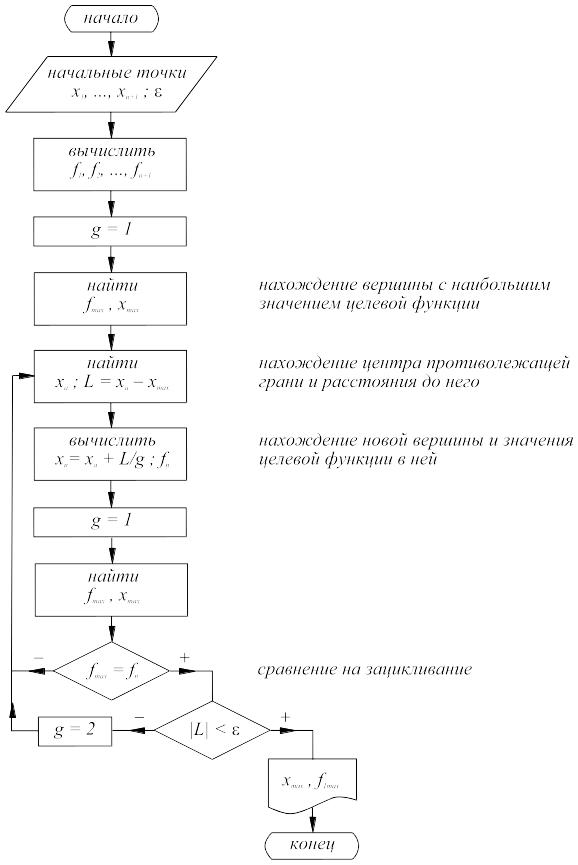
Рис. 14.1. Блок-схема симплексного метода

Вычислим f(x₀)=f₀ .

Г. При поиске минимума следует начать перемещение от точки х_h. Отразив точку х_h относительно точки х₀, получим точку х_r и найдем f(х_r) = f_r.

Операция отражения иллюстрируется рис. 14.2. Если  > 0 – коэффициент отражения, то положение точки x_r определяется следующим образом:

х_r = (1 + ) х₀ –   х_h.

Д. Сравним значения функций f_r и f_l.

1. Если f_r < f_l, то получим наименьшее значение функции. Направление из точки х₀ в точку х_r наиболее удобно для перемещения. Тогда мы производим растяжение в этом направлении и находим точку х_e и значение функции f_e = f(x_e). Рисунок 14.3 иллюстрирует операцию растяжения симплекса. Коэффициент растяжения  > 1 можно найти из следующих соотношений:

x_e – x₀ =  (x_r – x₀),

т.е. x_e =  x_r + (1 –  )x₀.

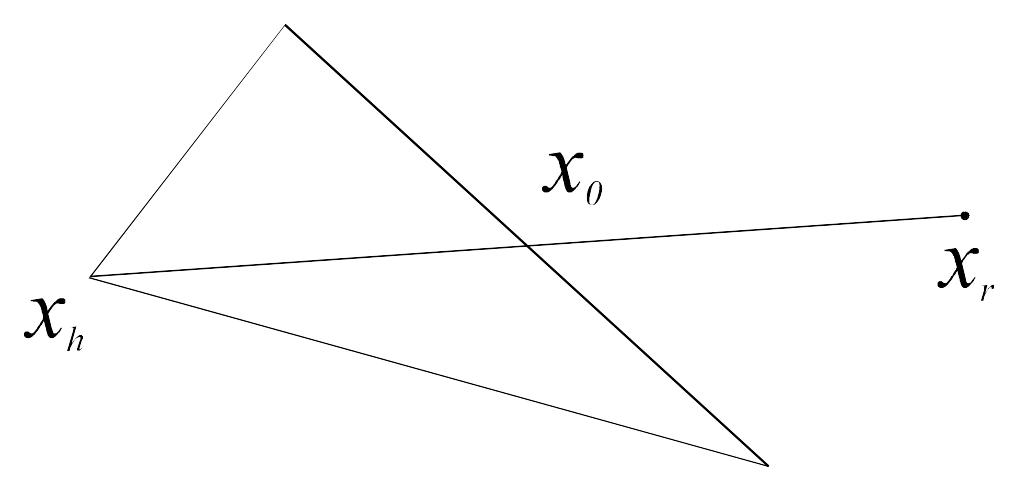
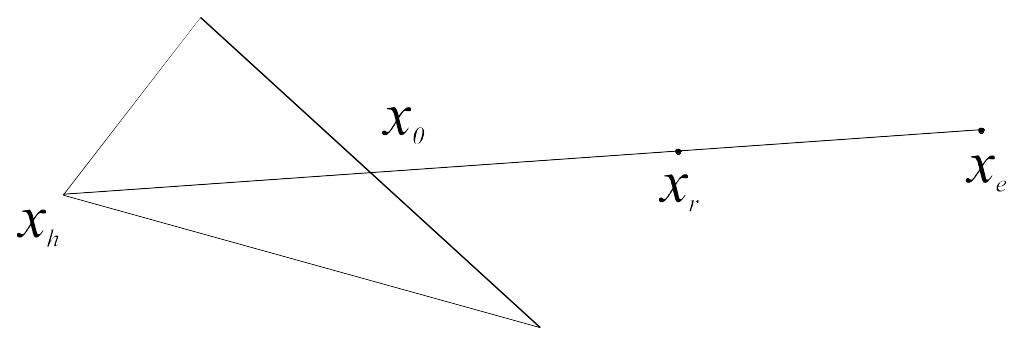
Рис. 14.2 Рис. 14.3

где  = |x_e – x₀|/ |x_r – x₀|.

а) Если f_e < f_l, то заменяем точку x_h на точку x_е и проверяем (n+1)-ую точку симплекса на сходимость к минимуму (см. шаг 3). Если сходимость достигнута, то процесс останавливается; в противном случае возвращаемся на шаг Б.

б) Если f_e > f_l, то отбрасываем точку f_e. Очевидно, мы переместились слишком далеко от точки x₀ к точке x_r. Поэтому следует заменить точку x_h на точку x_r, в которой было получено улучшение (шаг Д1), проверить сходимость и, если она не достигнута, вернуться на шаг В.

2. Если f_r > f_l, но f_r < f_g, то x_r является лучшей точкой по сравнению с другими двумя точками симплекса и мы заменяем точку x_h на точку x_r и, если сходимость не достигнута, возвращаемся на шаг Б, т.е. выполняем пункт 1б, описанный выше.

3. Если f_r > f_l, но f_r > f_g, то перейдем на шаг Е.

Е. Сравним значения функций f_r и f_h.

1. Если f_r > f_h, то переходим непосредственно к шагу сжатия Е2. Если f_r<f_h, то заменяем точку x_h на точку x_r и значение функции f_h на значение функции f_r. Запоминаем значение f_r > f_g из шага Д2, приведенного выше. Затем переходим на шаг Е2.

2. В этом случае f_r > f_h, поэтому ясно, что мы переместились слишком далеко от точки x_h к точке x₀. Попытаемся исправить это, найдя точку x_c (а затем f_c) c помощью шага сжатия, показанного на рис. 14.4.

Если f_r > f_h, то сразу переходим к шагу сжатия и находим точку x_c из соотношения

x_c – x₀ =  (x_h – x₀),

где  (0 <  < 1) – коэффициент сжатия. Тогда x_c =  x_h + (1 – ) x₀.

Если f_r < f_h, то сначала заменим точку x_h на точку x_r, затем произведем сжатие. Тогда точку x_c найдем из соотношения

x_c – x₀ =  (x_r – x₀), т.е.

x_c =  x_r + (1 – ) x₀

(рис. 14.5).

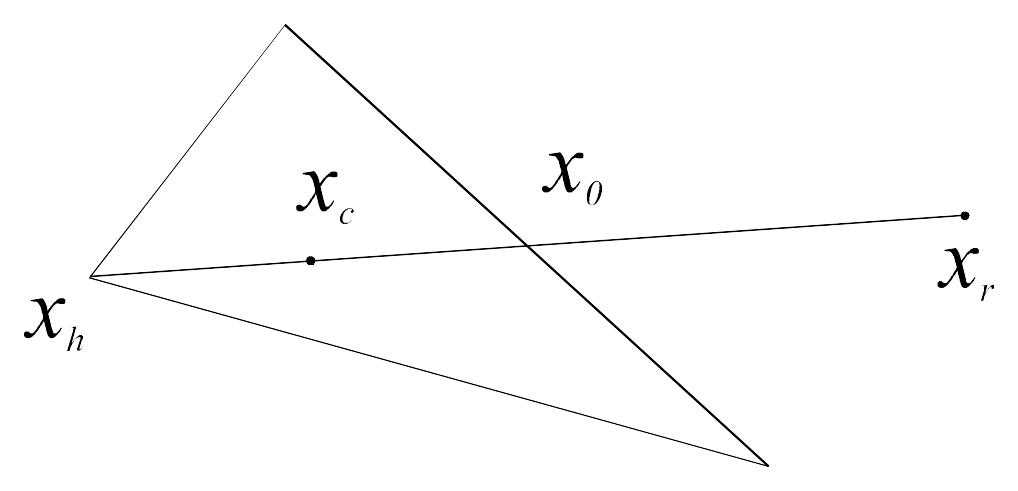
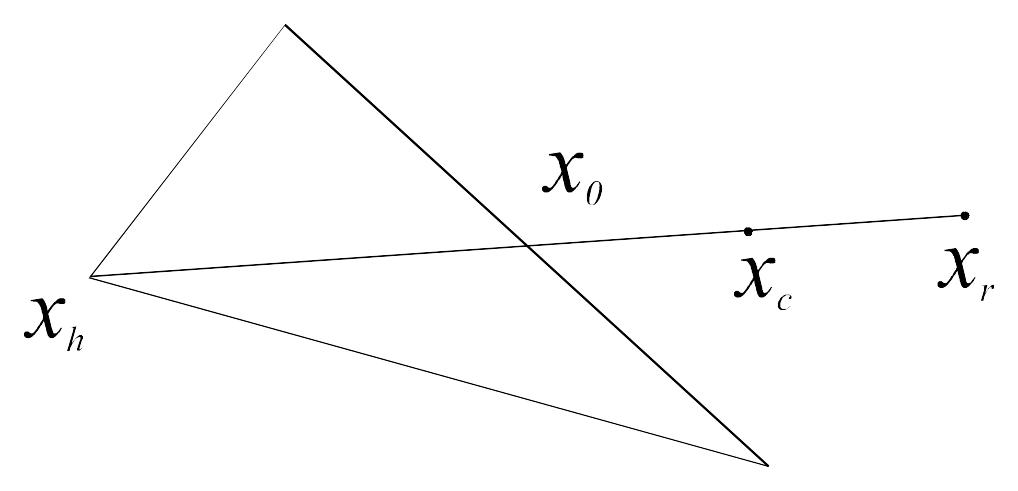
Рис. 14.4 Рис. 14.5

Ж. Сравним значения функций f_c и f_h.

1. Если f_c<f_h, то заменяем точку x_h на x_c, и если сходимость не достигнута, то возвращаемся на шаг Б.

2. Если f_c>f_h, то очевидно, что все наши попытки найти значение меньшее f_h закончились неудачей, поэтому мы переходим на шаг З.

З. На этом шаге мы уменьшаем размерность симплекса делением пополам расстояния от каждой точки симплекса до x_l-точки определяющей наименьшее значение функции.

Таким образом, точка x_i заменяется на точку x_i+1/2(x_i–x_l), т.е. заменяем точку x_i точкой 1/2 (x_i + x_l).

Затем вычисляем f_i для i = 1,2,..., (n + 1), проверяем сходимость и, если она не достигнута, возвращаемся на шаг В.

И. Проверка сходимости основана на том, чтобы стандартное отклонение (n+1)-го значения функции было меньше некоторого заданного малого значения . В этом случае вычисляется

, где .

Если  < , то все значения функции очень близки друг к другу и поэтому они, возможно, лежат вблизи точки минимума функции x_l.

Шаги этой процедуры представлены в виде блок-схемы на рис. 14.6.

2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Работа выполняется в такой последовательности:

• составляют подпрограмму для расчета выбранной целевой функции;

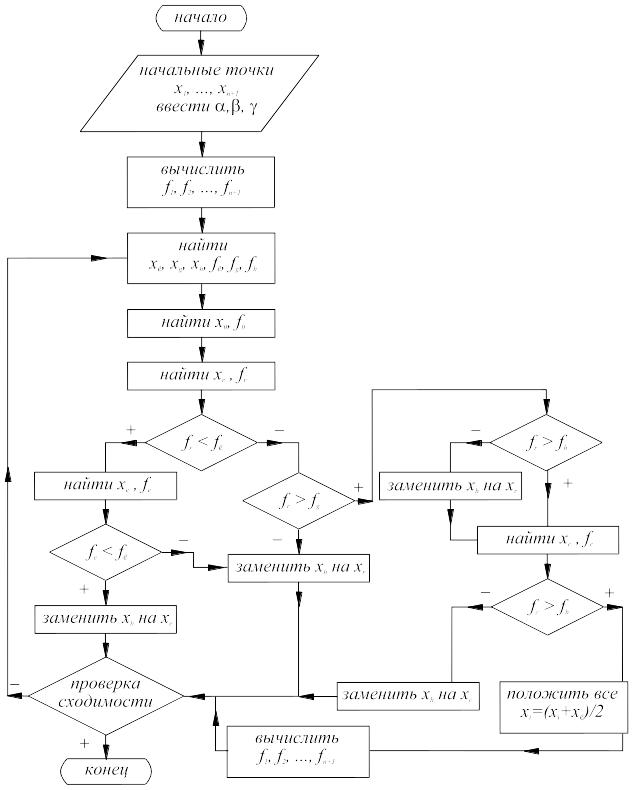
Рис. 14.6. Блок-схема метода Нелдера-Мида

• выполняют расчеты на ЭВМ по программе "SIMPL_M.BAS" (реализующей симплексный метод) и по программе "NED_MID.BAS" (реализующей метод Нелдера-Мида), находящихся в директории LABS, в результате которых определяют значение минимума целевой функции;

• дается оценка сравнения эффективности методов.

2.1 Составление подпрограммы для расчета целевой функции

Расчет целевой функции выполняется процедурой-подпрограммой, которую нужно составить на языке QuickBASIC.

В качестве примера приводится текст процедуры расчета следующей целевой функции:

Z = 100  (x₂ – x₁ ²)² + (1 – x₁)².

Для программы "SIMPL_M.BAS":

REM Function

Fun1:

Z = 100 * (x(2) – x(1) ^ 2) ^ 2 + (1 – x(1)) ^ 2

RETURN

Для программы "NED_MID.BAS":

2340 END

5000 Z = 100 * (X(2) - X(1) ^ 2) ^ 2 + (1 - X(1)) ^ 2

5060 TEV = TEV + 1

5100 RETURN

2.2. Работа с головными программами "SIMPL_M.BAS" и "NED_MID.BAS"

Ввод исходных данных в этих программах организован в диалоговом режиме. Поэтому для запуска необходимо на диске U в директории LANG\QBX\BIN найти и запустить головной файл qbx.exe, после чего открыть файл "SIMPL_M.BAS" или "NED_MID.BAS". Находясь в режиме редактирования составить и записать подпрограмму для расчета целевой функции. Комбинацией клавиш Shift+F5 запустить измененную программу в работу.

В качестве исходных данных для программы "SIMPL_M.BAS" необходимо задать: число переменных, точность вычислений, координаты n+1 вершины симплекса. Для программы "NED_MID.BAS" задаются: начальное приближение, длина шага, вводятся значения ALFA, BETA, GAMMA (через запятую). Рекомендуется брать ALFA = 1, BETA = 0.5, GAMMA = 2.

3. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

целевые функции и область изменения параметров приведены в табл. 13.1. Номер варианта соответствует порядковому номеру фамилии студента по журналу.

4. ОФОРМЛЕНИЕ ПРОТОКОЛА

В протоколе по лабораторной работе формулируется цель работы, описываются результаты расчетов, выполненных на ЭВМ. В протокол включаются листинг подпрограмм и результаты расчетов, блок-схема программы, реализующей симплексный метод и метод Нелдера-Мида.

5. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Классификация методов решения задач оптимизации.

2. Общая идея методов нелинейного программирования.

3. Симплексный метод, алгоритм расчета.

4. Блок-схема симплексного метода.

5. Метод Нелдера-Мида, алгоритм расчета.

6. Физический смысл операции отражения, растяжения и сжатия.

7. Сравнение метода Нелдера-Мида и симплексного метода.

8. Признак зацикливания симплексного поиска, условие окончания поиска.