
- •Электрические фильтры. Основные определения.
- •Области применения фильтров. Требования к фильтрам.
- •Частотная характеристика пассивных rc-фильтров
- •Введение в активные фильтры.
- •В частотной области:
- •В о временной области.
- •Типы фильтров.
- •5.1. Фильтры Баттерворта и Чебышева.
- •5.2. Фильтры Бесселя.
- •5.3. Сравнение фильтров.
- •Исследование электрических схем с использованием персонального компьютера
- •Обзор программы FilterLab для исследования активных фильтров на оу
- •7.1. Общие сведения.
- •7.2. Обзор основных элементов программы.
- •7.2.1. Главное меню программы.
- •7.2.2. Назначение кнопок и объектов программы.
- •7.2.3. Описание главного окна программы.
- •7.3. Теория сглаживающих фильтров.
- •Ход работы
- •Создание активного фильтра с помощью мастера фильтрации.
- •Сравнение параметров элементов различных типов фильтров.
- •Содержание отчета
- •Контрольные вопросы
- •Список литературы
Министерство образования РФ
СЕВМАШВТУЗ
Кафедра №6.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
По выполнению лабораторной работы №11
«Исследование амплитудно-частотных характеристик активных фильтров»
по дисциплине «Полупроводниковые преобразователи»
Индекс в соответствии с У.П.2000 г. Количество часов – 2 часа
ДС 05 специальность 140400
Северодвинск
2001
ИССЛЕДОВАНИЕ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК АКТИВНЫХ ФИЛЬТРОВ
ЦЕЛЬ РАБОТЫ:
1. Получить общие теоретические сведения об активных фильтрах.
2. Научиться задавать требуемый фильтр и исследовать его АЧХ с помощью программы FilterLab.
ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Электрические фильтры. Основные определения.
В работе измерительных систем и систем автоматического регулирования часто необходимо выделение полезного сигнала из шума или смеси других сигналов, имеющих спектральный состав, отличный от спектра полезного сигнала.
Эта задача решается при помощи различных электрических фильтров [4], назначение которых — выделение и передача определённой области амплитудно-частотного спектра входного сигнала (например, напряжения) таким образом, чтобы все спектральные компоненты выходного сигнала (напряжения) находились только в указанной области. Эта область называется областью прозрачности, или областью пропускания фильтра. Спектральные компоненты выходного сигнала (амплитуды гармонических составляющих выходного напряжения) заданным образом связаны с величиной спектральных составляющих на входе фильтра (амплитудами гармоник входного напряжения), лежащих в области прозрачности; эта зависимость определяется видом амплитудно-частотной характеристики фильтра в области пропускания. Спектральные компоненты входных сигналов, лежащие вне области прозрачности, в идеальном случае должны полностью отсутствовать в выходном сигнале; практически же они в небольшой мере имеются на выходе фильтра, и их зависимость от входного сигнала определяется видом амплитудно-частотной характеристики (АЧХ) вне области пропускания (в так называемой переходной области и в области непрозрачности, или области задерживания) фильтра.
Вид АЧХ должен соответствовать требованиям, которые предъявляются к фильтру как элементу информационной системы, т. е. определяется назначением фильтра. Например, может требоваться характеристика резонансного контура с чрезвычайно узкой полосой пропускания или «столообразная» (прямоугольная) форма частотной характеристики, фильтра с постоянным значением коэффициента передачи сигнала в области прозрачности и с резким спадом коэффициента передачи при переходе в область непрозрачности. Однако вид частотной характеристики фильтра как элемента реальной аппаратуры определяется выбранной схемой, конструкцией, свойствами деталей и пр., что, в свою очередь, существенно зависит от условий применения фильтра. Практически коэффициент передачи реального фильтра всегда имеет частотно-зависимое отклонение (неравномерность) от постоянного значения в области прозрачности, а за границей этой области — монотонный спад до некоторого конечного значения, соответствующего началу области непрозрачности. С дальнейшим углублением в область непрозрачности коэффициент передачи или продолжает монотонно уменьшаться или пульсирует, нигде не превышая того значения, которое он имел на границе области. Таким образом, между областью прозрачности и областью непрозрачности находится переходная область характеристики фильтра. Заметим, что требование крутого спада коэффициента передачи, т.е. узкой переходной области, является обычным требованием к фильтрам и характеризует их качество.
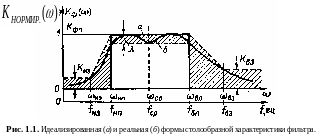
Сказанное
иллюстрируется на рис.1.1.
Здесь желаемой формой амплитудно-частотной
характеристики является прямоугольник
(контур а), т. е. в области (зоне) прозрачности
![]() (
(![]() и
и
![]() —
соответственно
нижняя и верхняя её границы) модуль
коэффициента передачи фильтра
—
соответственно
нижняя и верхняя её границы) модуль
коэффициента передачи фильтра
![]()
![]() равен постоянной величине
равен постоянной величине
![]() ,
а вне её —
равен нулю.
Характеристика же реального фильтра
(кривая б)
отклоняется от прямоугольной формы.
Для удобства учёта этого отклонения
коэффициент передачи в полосе прозрачности
и частоту на границе амплитудно-частотной
характеристики проектируемого фильтра
нормируют:
,
а вне её —
равен нулю.
Характеристика же реального фильтра
(кривая б)
отклоняется от прямоугольной формы.
Для удобства учёта этого отклонения
коэффициент передачи в полосе прозрачности
и частоту на границе амплитудно-частотной
характеристики проектируемого фильтра
нормируют:
![]()
 ,
,
![]() ,
,
это позволяет строить графики АЧХ разных фильтров в одних координатных осях.
Тогда
неравномерность нормированного
коэффициента передачи АЧХ реального
фильтра в полосе прозрачности определяется
величиной
(обычно
=
1
–
30%). При fНОРМИР.
= 1 (что
соответствует границе полосы пропускания)
KНОРМИР.()
= 0,707 (или –3
дБ). Задаются
также границы областей (зон) задерживания
![]() и
и
![]() (
и
—
соответственно
нижняя и верхняя ее границы), на которых
модуль нормированного коэффициента
передачи не должен превышать соответственно
значений
(
и
—
соответственно
нижняя и верхняя ее границы), на которых
модуль нормированного коэффициента
передачи не должен превышать соответственно
значений
![]() <1
и
<1
и
![]() <1.
Между областью прозрачности и зонами
задерживания находятся переходные
области
<1.
Между областью прозрачности и зонами
задерживания находятся переходные
области
![]() и
и
![]()
,
в которых нормированный коэффициент
передачи
KНОРМИР.()
должен монотонно уменьшаться от
1
до значений
КНЗ
и КВЗ.
Таким образом, реальная амплитудно-частотная
характеристика фильтра (кривая б)
должна лежать в заштрихованной области
рис.1.1.
Величины ,
КНЗ,
,
,
,
,
КВЗ
определяющие границы этой области,
будем называть параметрами
АЧХ фильтра.
,
в которых нормированный коэффициент
передачи
KНОРМИР.()
должен монотонно уменьшаться от
1
до значений
КНЗ
и КВЗ.
Таким образом, реальная амплитудно-частотная
характеристика фильтра (кривая б)
должна лежать в заштрихованной области
рис.1.1.
Величины ,
КНЗ,
,
,
,
,
КВЗ
определяющие границы этой области,
будем называть параметрами
АЧХ фильтра.
Характеристика,
изображённая на рис.1.1,
является характеристикой
полосно-пропускающего фильтра (ППФ),
или полосового
фильтра
(ПФ). Полосовой
фильтр может, в частности, обладать
симметричной характеристикой, у которой
![]() ,
,
![]() .
.
Заграждающий фильтр (ЗФ) на интервале частот от до имеет область заграждения.
Фильтр нижних частот (ФНЧ) имеет область прозрачности от 0 ( = 0) до некоторой конечной частоты , а фильтр верхних частот (ФВЧ) пропускает частоты от некоторой конечной частоты до бесконечности ( = ).
Четыре перечисленных вида фильтров: ФНЧ, ФВЧ, ПФ, ЗФ — позволяют на практике решать любые задачи по фильтрации сигналов.
