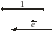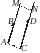- •Глава 3. Линейные пространства Глава 3. Линейные пространства
- •3.1. Линейные операции над векторами
- •Вопросы и упражнения
- •3.2. Линеал
- •Вопросы и упражнения
- •3.3. Линейная зависимость и независимость векторов
- •Вопросы и упражнения
- •3.4. Геометрический смысл линейной зависимости и независимости векторов на плоскости и в трехмерном пространстве
- •Вопросы и упражнения
Глава 3. Линейные пространства Глава 3. Линейные пространства
3.1. Линейные операции над векторами
Вектором называют отрезок, для которого указано, какая из его граничных точек является начальной и какая — конечной. Начальную точку называют началом (точкой приложения) вектора, а конечную — концом вектора.
Под направлением вектора понимают направление от его начала к концу. Направление отмечается стрелкой, помещаемой у конца вектора (рис. 3.1.1).
Длина или модуль вектора есть длина соответствующего отрезка, определяющего данный вектор.
Вектор с началом
А
и концом В
обозначают символом
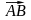 .
Иногда вектор обозначают одной буквой
со стрелкой, помещенной сверху этой
буквы, например,
.
Иногда вектор обозначают одной буквой
со стрелкой, помещенной сверху этой
буквы, например,
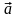 (рис. 3.1.1).
Длину вектора обозначают соответственно
как |
(рис. 3.1.1).
Длину вектора обозначают соответственно
как |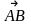 |,
|
|
и т. д.
|,
|
|
и т. д.
Вектор
называют
нулевым,
если его начало и конец совпадают.
Нулевой вектор обозначают обычно
символом
 .
Нулевой вектор не имеет определенного
направления (направление произвольно)
и его длина равна нулю: |
|= 0.
.
Нулевой вектор не имеет определенного
направления (направление произвольно)
и его длина равна нулю: |
|= 0.
Вектор называют единичным, если его длина равна единице в принятой системе измерения (рис. 3.1.2).
Векторы называются компланарными, если они расположены в одной плоскости или в параллельных плоскостях.
Векторы коллинеарны, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 3.1.3). Нулевой вектор считают коллинеарным любому вектору.
Рис. 3.1.1 |
Рис. 3.1.2 |
Рис. 3.1.3 |
Рис. 3.1.4 |
Два коллинеарных
вектора
и
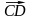 называются сонаправленными,
если для любых точек M
и N,
выбранных
на лучах, определенных этими векторами,
при условии, что
называются сонаправленными,
если для любых точек M
и N,
выбранных
на лучах, определенных этими векторами,
при условии, что
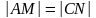 ,
расстояние
,
расстояние
 не меняется
(рис. 3.1.4).
не меняется
(рис. 3.1.4).
Для сонаправленных
векторов будем использовать обозначение
 .
Два коллинеарных, но не сонаправленных
вектора, называются противоположно
направленными
(обозначение
.
Два коллинеарных, но не сонаправленных
вектора, называются противоположно
направленными
(обозначение
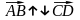 ).
).
Теорема 3.1.1. Два вектора, сонаправленных с третьим, сонаправлены друг с другом:
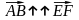 ,
,
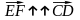
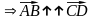 .
.
Доказательство.
Очевидно, что
и
коллинеарны. Так как
,
то для любых точек M
и P
таких, что
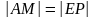 расстояние
расстояние
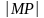 не меняется. Поскольку
,
то для любых точек N
и
P
таких, что
не меняется. Поскольку
,
то для любых точек N
и
P
таких, что
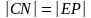 расстояние
расстояние
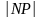 не меняется. Но тогда
и расстояние
не меняется. Поэтому
не меняется. Но тогда
и расстояние
не меняется. Поэтому
 .
.
Ортом
ненулевого вектора
называют вектор
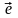 :
:
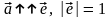 .
.
Векторы
равны,
если они сонаправлены и имеют одинаковую
длину (векторы
и
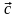 ,
рис. 3.1.3).
Для равных векторов
и
используют обозначение
,
рис. 3.1.3).
Для равных векторов
и
используют обозначение
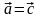 .
.
Векторы
противоположны,
если они противоположно направлены и
имеют одинаковую длину (векторы
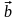 и
и
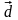 ,
рис. 3.1.3).
Для противоположных векторов
и
используют обозначение
,
рис. 3.1.3).
Для противоположных векторов
и
используют обозначение
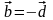 .
.
Ясно, что если
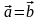
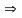
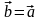 (коммутативность),
(коммутативность),
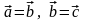 (транзитивность).
(транзитивность).
Заметим, что равенство векторов определено с точностью до их положения в пространстве. Иными словами, мы не различаем двух равных векторов, имеющих разные точки приложения. В дальнейшем будем рассматривать свободные векторы, т. е. векторы, точки приложения которых произвольны.
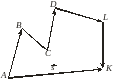
Говорят, что векторы следуют друг за другом, если начало каждого из них, начиная со второго, совпадает с концом предыдущего вектора (рис. 3.1.5).
Суммой векторов, следующих друг за другом, называется вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего вектора.
На рис. 3.1.6 представлена сумма
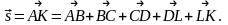
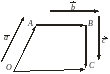
Суммой произвольно расположенных векторов называется сумма векторов, следующих друг за другом, построенных, начиная с некоторой точки О, и равных соответственно данным векторам (рис. 3.1.7).
Рис. 3.1.5 |
Рис. 3.1.6 |
Рис. 3.1.7 |
Сумма произвольно расположенных векторов не зависит от того, как выбрана начальная точка О при построении векторов, следующих друг за другом.
Сумма векторов определяется однозначно и обладает очевидными свойствами:
1.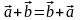 (коммутативность).
(коммутативность).
2.
(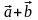 ) +
=
+ (
) +
=
+ (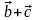 )
) (ассоциативность).
(ассоциативность).
3.
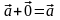 (особая роль
нулевого вектора).
(особая роль
нулевого вектора).
4. 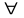
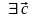 :
:
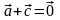 (существование
противоположного вектора).
(существование
противоположного вектора).
Р

Рис.3.1.8
азностью векторов и называют такой вектор , который в сумме с вектором дает вектор : + = (рис. 3.1.8). Разность векторов обозначается =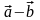 .
.
Произведением
вектора
на
вещественное число
называется вектор
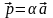 :
:
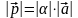 ;
;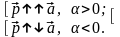
Если
= 0
или
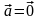 ,
то вектор
=
.
,
то вектор
=
.
Если
— орт вектора
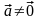 ,
то
,
то
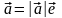 ,
откуда
,
откуда
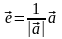 .
.
Произведение вектора на число определяется однозначно и обладает следующими свойствами:
1) 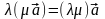 (ассоциативность);
(ассоциативность);
2) 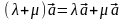 (дистрибутивность
относительно суммы чисел);
(дистрибутивность
относительно суммы чисел);
3) 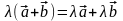 (дистрибутивность
суммы векторов);
(дистрибутивность
суммы векторов);
4) 1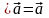 (наличие
единицы).
(наличие
единицы).
Рассмотренные операции (сложение векторов и умножение вектора на вещественное число) называются линейными операциями над векторами.
Теорема 3.1.2.
Ненулевые
векторы
и
коллинеарны тогда и только тогда, когда
найдется такое число 0,
что вектор
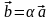 .
.
Доказательство. Достаточность. Непосредственно следует из определения произведения вектора на число.
Необходимость.
Рассмотрим
векторы
и
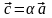 ,
где
,
где

По
построению
векторы
 ,
,
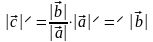 =
.
=
.