Порядок выполнения эпюра

1.Для задачи 2-3 выполняем две проекции отрезка АВ по заданным координатам.

2.Задаем ось вращения i перпендикулярно к горизонтальной плоскос­ти проекций и в конце отрезка АВ.

3.Вращая отрезок АВ вокруг оси i, получаем его натуральную величину a’₁b’₁, на которой строим искомую точку С’₁, откладывая b’₁c’₁=50мм, и обратным проецированием находим ее проекции С’, C.

4. Для задачи 2-4 выполняем две проекции точек А, В, С, Д по заданным координатам, соединяем точки ABC, ДВС: получаем горизонтальную и фронтальную проекции двугранного угла АВСД (abсd, a'b'c'd').,

5.Задаем ось х₁ параллельно горизонтальной проекции ребра ВС (bс) двугранного угла и в результате первой замены плоскости V на плоскость Р получаем натуральную величину ребра b_pc_p.

6.Задаем ось х₂ перпендикулярно новой проекции ребра ВС(b_pc_p) и, в результате второй замены плоскости Н на плоскость S, получаем вырожденную в точке проекцию ребра b_│c_│ и вырожденные в прямые плоскости двугранного угла, т.е. получаем действительную величину двугранного угла.

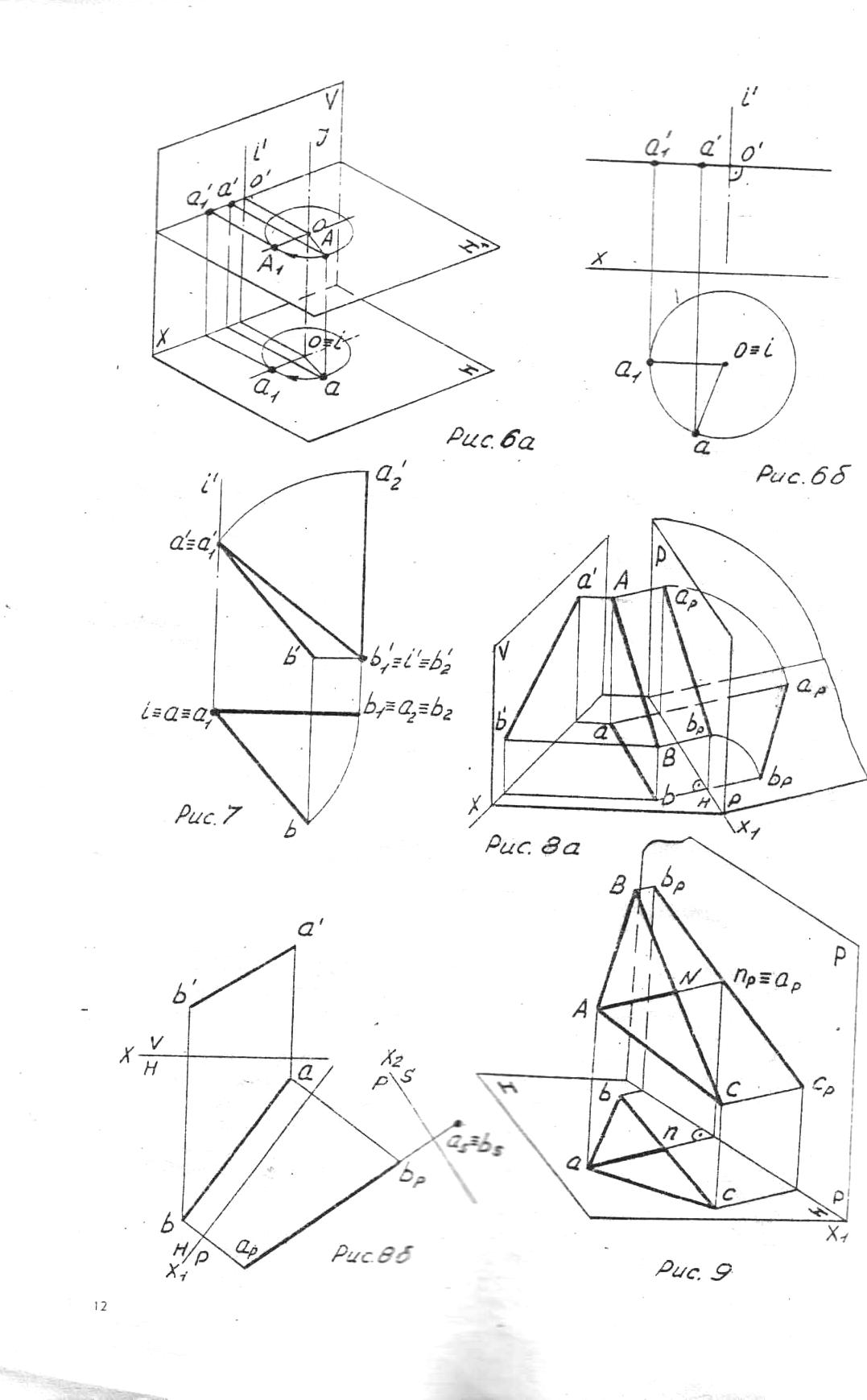
7.Для задачи 2-5 выполняем две проекции треугольника АВС( abc, a’b’c’) по заданным координатам и строим в треугольнике горизонталь А1(а’1’││ox).

8.Задаем ось Х перпендикулярно горизонтальной проекции горизонтали А1 (а1) и в результате первой замены плоскости V на плоскость P получаем вырожденную в отрезок проекцию треугольника а_рb_pc_p, который перпендикулярен к плоскости Р.

9.Задаем ось Х₂ параллельно новой проекции треугольника а_рb_pc_p и в ре­зультате замены плоскости Н на плоскость S, параллельную треугольнику ABC, получаем натуральную величину треугольника а_sb_sc_s, в котором и находим его ортоцентр О_s. Обратным проецированием находим проекции ортоцентра о_p; о; o’.

Эпюр №3

Тема: Способы преобразования эпюра: плоскопараллельное перемещение, вращение вокруг линии уровня.

Содержание: Эпюр содержит решение двух задач.

Задача 6. Найти центр О (о’, о) окружности, описанной около треугольника ABC. Задачу решить способом плоскопараллельного перемещения.

Задача 7. Определить натуральный вид треугольника ABC. Задачу решить способом вращения линии уровня.

Координаты для точек задач 6, 7 взять из таблицы 1. Образец вы­полнения задания на чертеже 3.

Пояснения. Плоскопараллельное перемещение можно рассматривать как вращение вокруг невыявленных осей, перпендикулярных к плоскостям проекций. Все точки геометрического объекта в этом способе перемещаются во взаимно па­раллельных плоскостях, а теорема способа читается следующим образом.

При плоскопараллельном перемещении геометрического объекта одна из его проекций, не изменяясь, перемещается в плоскости проекций, другие проекции точек геометрического объекта перемещаются по прямым, парал­лельным направлению оси проекций.

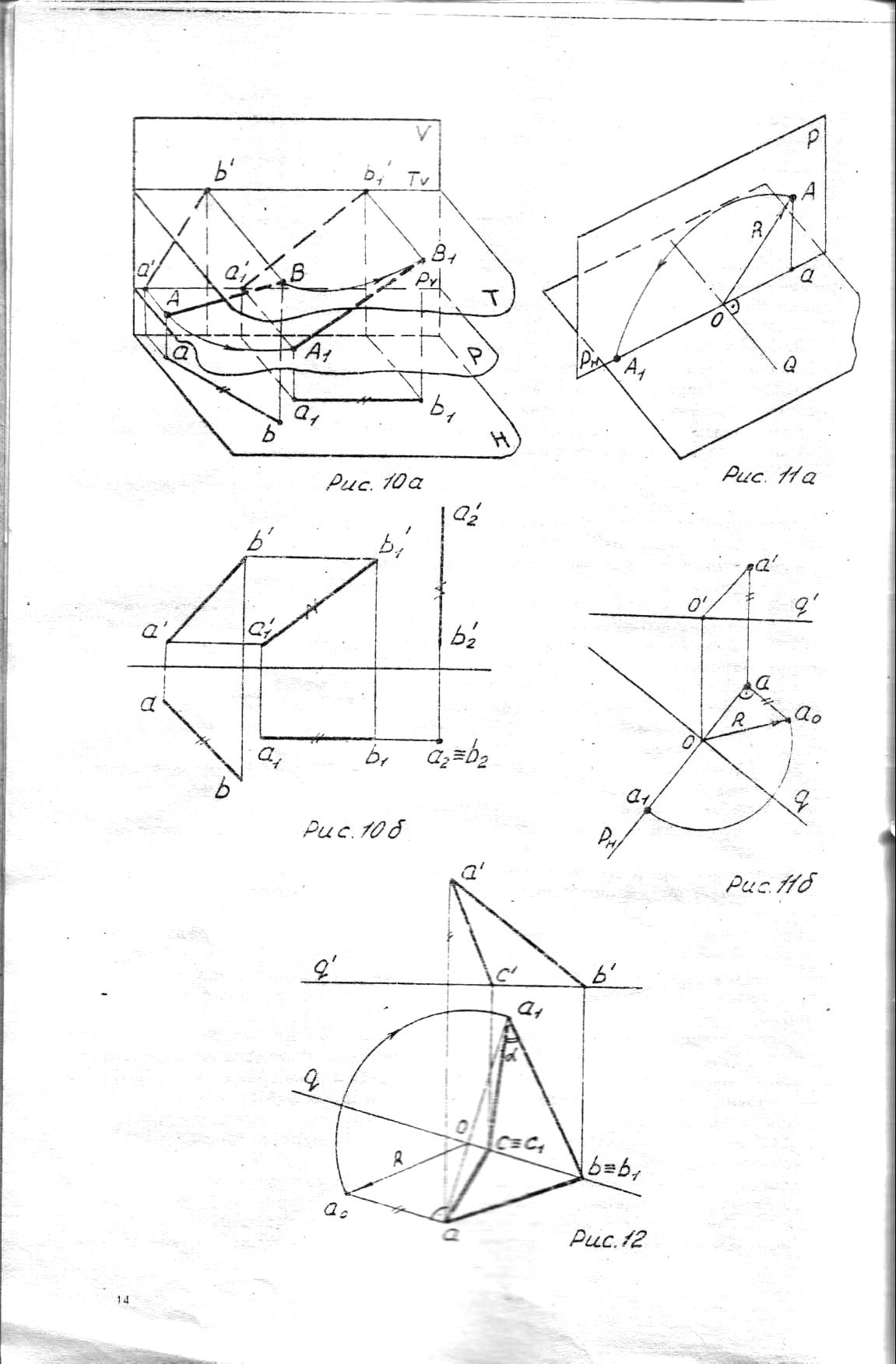
В решении ряда метрических задач требуется преобразовать прямую общего положения в прямую уровня, а затем — в проецирующую, выполнив при этом последовательно два преобразования. Рассмотрим решение этой за­дачи Пусть дан отрезок AB (ab, a’b'), рис. 10.

Если переместить горизонтальную проекцию ab отрезка в положение a’b', параллельное оси проекций, то вторая ее проекция а'₁b'₁ натуральной ве­личине отрезка. Проекции а'₁ и b'₁ прямой в смещенном положении определя­ем на линиях связи и горизонтальных прямых (на следах плоскостей движения этих точек).

Перемещая фронтальную проекцию а'₁b'₁ в положение а'₂b'₂ и определяя горизонтальную проекцию отрезка а'₂b'₂, получим новое положение прямой, перпендикулярное горизонтальной плоскости проекций.

Применение способа плоскопараллельного перемещения к определению натуральной величины плоскости, например, треугольника, аналогично спосо­бу замены плоскостей проекций, выполняя решение задачи с помощью линии уровня плоскости, например горизонтали (см. образец решения задачи 6 на чер. 3).

Способ вращения вокруг линии уровня применяется для преобразования плоскости общего положения в плоскость уровня и для определения действи­тельной величины плоской фигуры. Задача решается одним вращением вокруг линии уровня данной плоскости (горизонтали или фронтали).

Для уяснения рассмотрим вращение точки вокруг горизонтальной прямой (рис. 11а) до совмещения с некоторой плоскостью Н, параллельной горизонтальной плоскости проекций Н.

Точка А вращаясь вокруг горизонтали Q, опишет дугу окружности, лежа­щую в плоскости проекций Р, перпендикулярной к этой прямой Q, как к оси вращения. Плоскость Р в данном случае горизонтально-проецирующая, поэ­тому горизонтальная проекция окружности, описываемой точкой А, на горизонтальной плоскости проекций совпадает с горизонтальным следом плоскости Р (Р_н). Центр вращения находится в точке О, в которой ось вращения Q (q) пересекает плоскость вращения Р (Р_н). Радиус вращения R точки А будет равен ОА. Новое положение точки А в плоскости Н, найдем на следе Р_н на расстоянии от оси вращения, равном ОА.

На рис. 11б для нахождения нового положения точки А необходимо определить натуральную величину радиуса вращения способом прямоуголь­ного треугольника. В прямоугольном треугольнике оаа_о, одним катетом оа яв­ляется горизонтальная проекция — радиуса R, вторым аа_о — высота точки А относительно горизонтальной плоскости Н, взятой с фронтальной проекции. Гипотенуза треугольника оа_о является истинной величиной радиуса вращения.

На рисунке 12 показано применение данного метода в определении вели­чины угла между двумя пересекающимися прямыми АВ и ВС, где вращаем точку А вокруг линии уровня (горизонтали) данного угла ВАС.