ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

«ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра высшей математики

Математика Функции двух и трех переменных

Методические указания и контрольные задания

для студентов дневной формы обучения строительных специальностей

Факультет инженерно-строительный

Для всех специальностей

Вологда

2010

УДК: 511.147:511.61/62

Математика: Функции двух и трех переменных: методические указания и контрольные задания для студентов дневной формы обучения строительных специальностей. Вологда: ВоГТУ, 2010. –24 с.

В методических указаниях изложены основные задачи и методы их решения по теме «Функции двух и трех переменных», изучаемой студентами в курсе математики на инженерно-строительном факультете ВоГТУ. Перед изложением метода решения каждого типа задачи приведены краткие сведения из теории и необходимые формулы. В конце методических указаний приведены задачи, которые будут предложены студентам в контрольной работе по теме «Функции двух и трех переменных».

Утверждено редакционно-издательским советом ВоГТУ

Составитель: Н.В. Степанова, канд. физ.-мат. наук, доцент кафедры высшей математики ВоГТУ.

Рецензент: О.И Микрюкова, канд. физ.-мат. наук, доцент, зав. кафедрой высшей математики ВоГТУ.

Введение

Настоящие методические указания предназначены для студентов дневной формы обучения строительных специальностей. Их цель – помочь студентам в самостоятельном изучении материала по теме «Функции двух и трех переменных» и в подготовке к написанию контрольной работы по указанной теме.

§1. Функции двух и трех переменных

1.1. Частные производные функции двух и трех переменных

Сведения из теории

Изложение теоретических сведений начнем с введения понятия функции двух переменных. Пусть есть переменная с множеством значений . Есть также две независимые переменные и . Они принимают такие значения, при которых пары образуют плоскую область .

Определение Переменная называется функцией двух переменных и , если каждой паре значений по некоторому правилу или закону сопоставляется единственное значение .

Термины:  область определения функции; и  аргументы функции.

Везде далее мы будем рассматривать аналитический способ задания функции. Это значит, что правило, по которому паре значений сопоставляется единственное значение , задается с помощью формулы .

Определение функции трех переменных мало отличается от определения функции двух переменных.

Определение Переменная называется функцией трех переменных , и , если каждой тройке значений по некоторому правилу или закону сопоставляется единственное значение .

Область или (для функции 3-х переменных) называется областью определения функции. Строго говоря, она должна оговариваться в условии задачи. При аналитическом задании функции (с помощью формулы) этого часто не делается. В таком случае в качестве области определения берется область допустимых значений переменных формулы, с помощью которой функция задана. Такая область определения называется естественной.

Пример. Найти область определения функции .

Решение.

Найдем область допустимых значений формулы, задающей функцию:

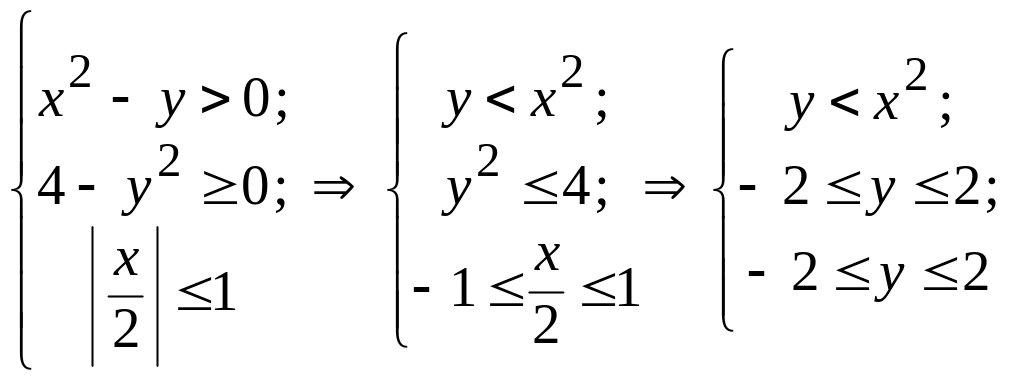
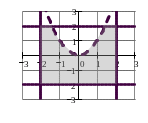
Ответ. Область определения функции  затемненная область на рисунке.

В теории функций одной переменной фундаментальным является понятие производной функции в точке. В теории функций 2-х и 3-х переменных фундаментальными являются понятия частных производных.

Рассмотрим два частных способа изменения переменных и для функции 2-х переменных.

Способ 1: изменяется, а фиксирована. При этом приращение переменной , обозначенное как , порождает приращение функции, задаваемое равенством . Оно называется частным приращением по , чтобы подчеркнуть, что изменяется только переменная .

Определение Частная производная (читается штрих по ) – это предел отношения частного приращения к приращению переменной при условии, что приращение , т.е.

.

Способ 2: изменяется, а фиксирована. При этом приращение переменной , обозначенное как , порождает приращение функции, задаваемое равенством . Оно называется частным приращением по , чтобы подчеркнуть, что изменяется только переменная .

Определение Частная производная (читается штрих по ) – это предел отношения частного приращения к приращению переменной при условии, что приращение , т.е.

.

Замечание В учебной литературе часто используется другое обозначение частных производных, а именно, и ( читается дэ z по дэ x, дэ z по дэ y ).

Определение частных производных функции трех переменных принципиально не отличается от определения частных производных функции двух переменных. Разница состоит только в том, что при нахождении частных производных функции трех переменных одна переменная изменяется, а две других считаются константами.

Техника вычисления частных производных основана на тех же правилах, что и техника нахождения производных функции одной переменной. Этого и следовало ожидать, поскольку при вычислении частной производной меняется только одна переменная, а другие не меняются и считаются константами. При этом функции 2-х и 3-х переменных фактически становятся функциями одной переменной.

Частными дифференциалами функции 2-х переменных называются произведения вида и . Полный дифференциал – это сумма частных дифференциалов, т.е. .

Пример. Найти частные производные и полный дифференциал функции 2-х переменных .

Решение. Начнем с частной производной . При ее вычислении считаем константой. Тогда функция становится функцией одной переменной , т.е. . Как функция она является произведением и дифференцируется как произведение.

После небольшого упрощения получаем .

Найдем . Теперь функция 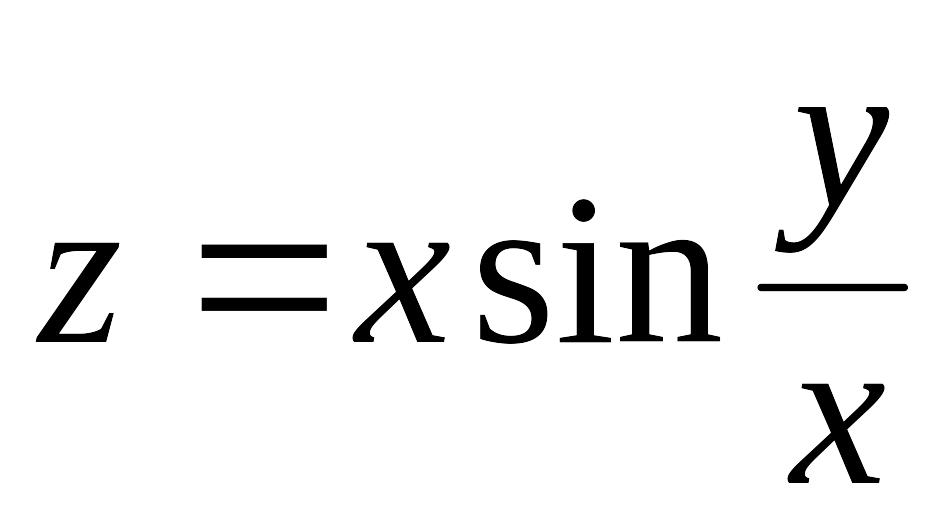становится функцией только от ,

а считается константой. По отношению к функция является обычным синусом. Тогда

.

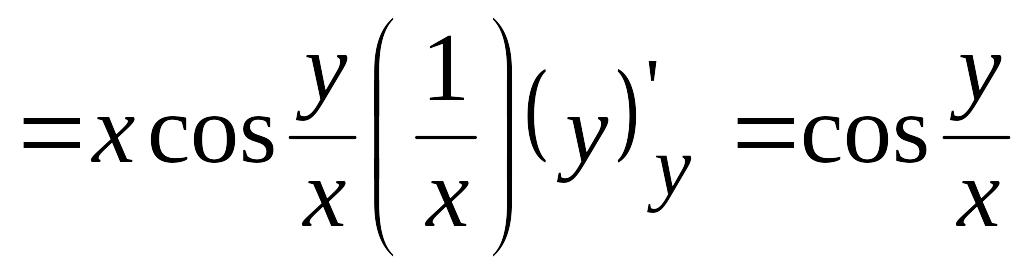Полный дифференциал функции будет иметь вид

Ответ. , ,

.

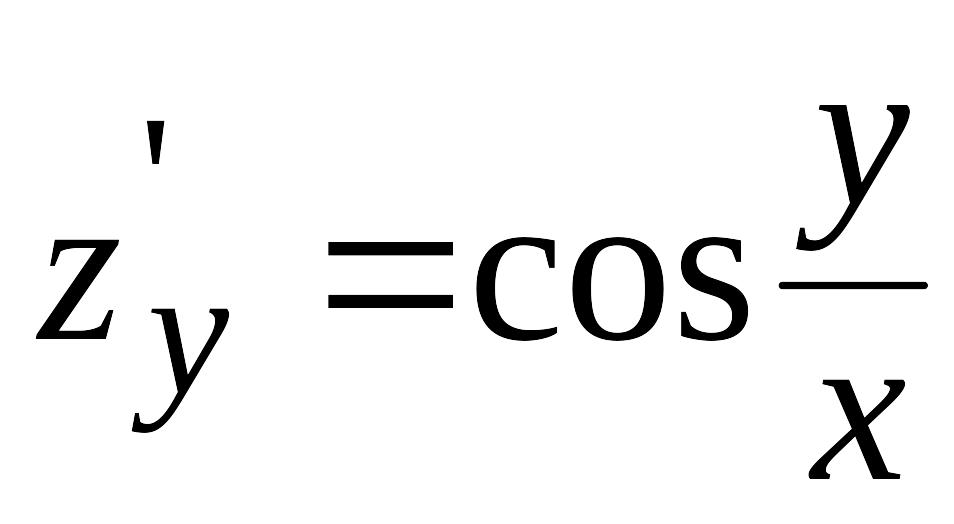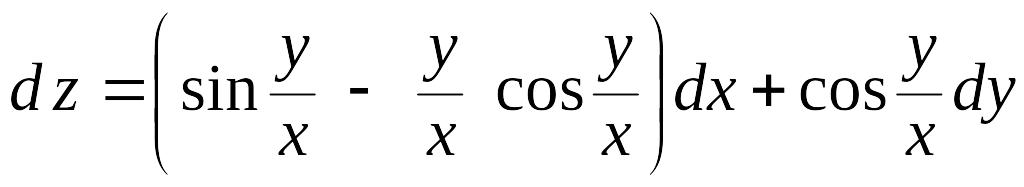Пример. Найти частные производные функции 3-х переменных

.

Решение. Начнем с частной производной .

.

Сведения из теории

Обратите внимание на то, что частные производные 1-го порядка и сами являются функциями 2-х переменных. Для функции 2-х переменных также как и для функции одной переменной введены понятия производных второго порядка. Следует подчеркнуть, что, если для функции одной переменной существует только одна производная второго порядка , то для функции 2-х переменных можно вычислить 4 частных производных 2-го порядка, а именно: , , , . Частные производные , называются смешанными частными производными 2-го порядка. Очень важен порядок записи переменных в нижнем индексе. Например, символ означает, что сначала функция дифференцируется по и получается , а затем уже новая функция 2-х переменных дифференцируется по , т.е. 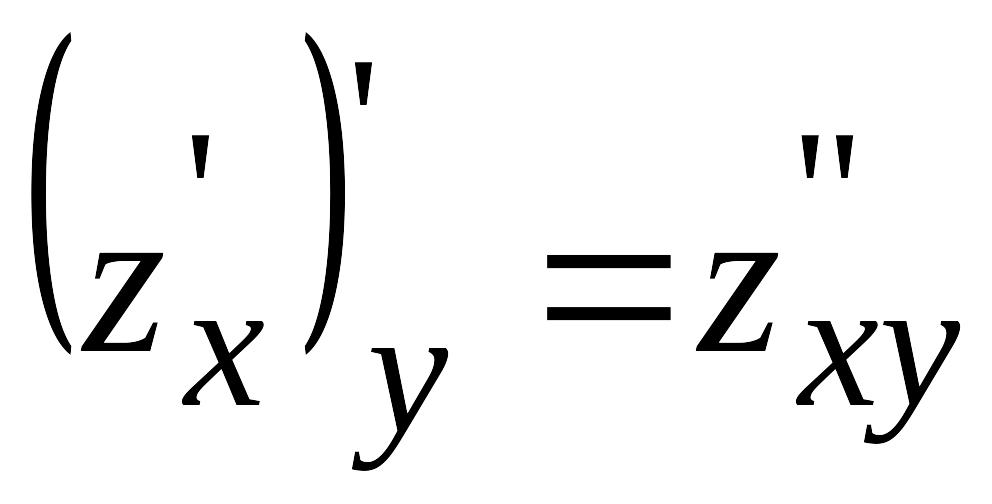. Не удивляйтесь, если получите, что . Это равенство справедливо во всех случаях, когда обе смешанные производные существуют.

Пример. Найти все частные производные 2-го порядка функции 2-х переменных

.

Решение.

В предыдущем примере были найдены частные производные первого порядка , . Вычислим , , , .

.

_.

. .

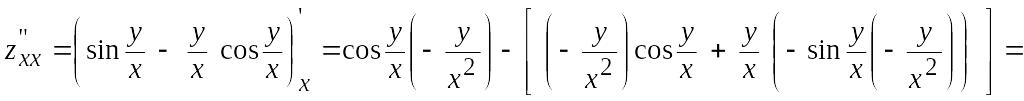
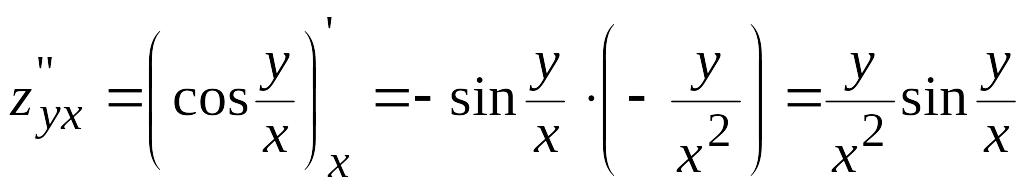Заметьте, как было сказано ранее, смешанные частные производные 2-го порядка не зависят от порядка дифференцирования, поэтому

.

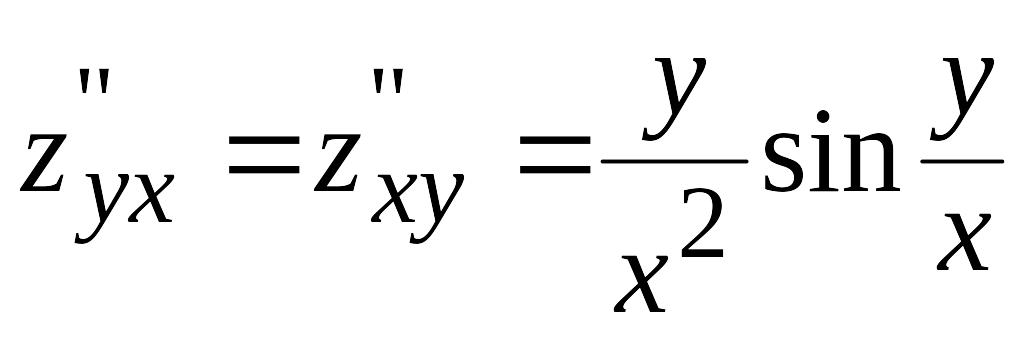Ответ. ; _; .

Пример. Установить, удовлетворяет ли функция данному дифференциальному уравнению в частных производных

.

Решение.

Функция удовлетворяет дифференциальному уравнению в частных производных, если при подстановке этой функции в данное дифференциальное уравнение оно преобразуется в тождественное равенство.

Предварительно вычислим все частные производные, которые входят в дифференциальное уравнение.

; .

Подставим найденные выражения производных в левую часть дифференциального уравнения.

Ответ. Функция удовлетворяет данному дифференциальному уравнению в частных производных.