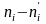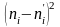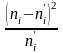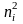- •Первичная обработка результатов наблюдений.
- •Построение выборочной ( эмпирической ) функции распределения.
- •III. Вычисление числовых характеристик
- •Выбор закона распределения.
- •V. Обоснование гипотезы о предполагаемом законе распределения.
- •Отыскание интервальных оценок параметров нормального закона.
- •Выводы.
- •(Необходимая для выполнения работы)
- •Вариант 9
- •Вариант 13
- •Вариант 15
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23.
- •Вариант 24.
V. Обоснование гипотезы о предполагаемом законе распределения.
По виду полигона и гистограммы (рис.1) было сделано предположение, что СВ Х подчинена нормальному закону. Из этого предположения удалось вычислить теоретические частоты и построить теоретическую кривую нормального распределения, что ещё более подтверждает, что генеральная совокупность СВ Х подчинена нормальному закону.
Однако
высказанную гипотезу ( называют её
нулевой
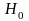 )
необходимо подтвердить, т.е. требуется
проверить согласованность имеющегося
эмпирического материала с предполагаемым
теоретическим распределением случайной
величины в генеральной совокупности.
)
необходимо подтвердить, т.е. требуется
проверить согласованность имеющегося
эмпирического материала с предполагаемым
теоретическим распределением случайной
величины в генеральной совокупности.
Проверка осуществляется с помощью специально подобранной случайной величины – критерия согласия.
Применим
критерий согласия
 -
« хи квадрат» (критерий Пирсона). С
этой целью будем сравнивать эмпирические
( наблюдаемые ) частоты
и теоретические частоты
по формуле
-
« хи квадрат» (критерий Пирсона). С
этой целью будем сравнивать эмпирические
( наблюдаемые ) частоты
и теоретические частоты
по формуле
 ………….
……………..(2)
………….
……………..(2)
Составим расчетную таблицу 9.
По
таблице критических точек распределения
( Гмурман В.Е., приложение 5) по заданному
уровню значимости
 и числу степеней свободы
и числу степеней свободы
 , где s
– число
частичных интервалов, r
- число
параметров предполагаемого распределения
СВ Х, найдём критическое значение
, где s
– число
частичных интервалов, r
- число
параметров предполагаемого распределения
СВ Х, найдём критическое значение
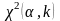 .
.
Таблица 9
|
|
|
|
|
Расчет для контроля |
|
|
|
|||||
2 3 7 8 15 9 4 2 |
1 3 7 11 12 9 5 2
|
1 0 0 -3 3 0 -1 0 |
1 0 0 9 9 0 1 0 |
1 0 0 0,82 0,75 0 0,2 0 |
4 9 49 64 225 81 16 4 |
4,00 3,00 7,00 5,82 18,75 9,00 3,20 2,00 |
50 |
50 |
|
|
2,77 |
|
52,77 |
В
нашем случае число степеней свободы
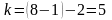 ,
а уровень значимости
= 0,05 ( по заданию). По приложению 5
находим:
,
а уровень значимости
= 0,05 ( по заданию). По приложению 5
находим:
В
таблице 9 найдено:
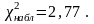
Так
как
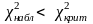 ,
то нет оснований для отклонения
гипотезы о нормальном распределении
генеральной совокупности СВ Х.
,
то нет оснований для отклонения
гипотезы о нормальном распределении
генеральной совокупности СВ Х.
Для
контроля вычислений формулу (2)
преобразуют к виду
 ;
имеем :
;
имеем :
Отыскание интервальных оценок параметров нормального закона.
Найдём
интервальные оценки математического
ожидания
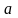 и среднего квадратического отклонения
и среднего квадратического отклонения
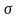 генеральной совокупности СВ Х.
генеральной совокупности СВ Х.
1). Для математического ожидания:
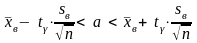 ,
,
где
n
- объём выборки,
-
выборочное среднее,
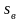 -
исправленное среднее квадратическое
отклонение.
-
исправленное среднее квадратическое
отклонение.
 -
находится по данной надёжности
(доверительной вероятности) и объёму
выборки n
по приложению 3 (см. Гмурман В.Е.). Приняв
за надёжность
-
находится по данной надёжности
(доверительной вероятности) и объёму
выборки n
по приложению 3 (см. Гмурман В.Е.). Приняв
за надёжность
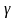 =
0,95 ( в соответствии с заданием ) , n
= 50,
получаем:
=
0,95 ( в соответствии с заданием ) , n
= 50,
получаем:
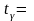 2,009.
Тогда
2,009.
Тогда
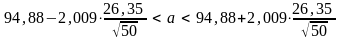 ,
,

т.е.
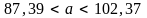 .
.
Итак, с надёжностью 0,95 математическое ожидание а заключено в доверительном интервале ( 87,39 ; 102,37 ).
2).
Доверительный интервал, покрывающий
среднее квадратическое
генеральной совокупности с заданной
надёжностью
, находится по формуле
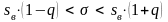 , если q
<
1 ……………….(3)
, если q
<
1 ……………….(3)
или
 ,
если q
>
1,
,
если q
>
1,
где - исправленное среднее квадратическое отклонение.
q находят по приложению 4 ( Гмурман В.Е. ) по данным n - объёму выборки и надежности . В нашем случае
 ,
,
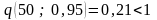 .
.
По
формуле (3) находим:
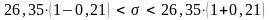 или
или
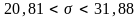 .
.
Следовательно, с вероятностью 0,95 можно утверждать, что среднее квадратическое отклонение генеральной совокупности изучаемой СВ Х заключено в интервале ( 20,81 ; 31,88 ).