
- •Первичная обработка результатов наблюдений.
- •Построение выборочной ( эмпирической ) функции распределения.
- •III. Вычисление числовых характеристик
- •Выбор закона распределения.
- •V. Обоснование гипотезы о предполагаемом законе распределения.
- •Отыскание интервальных оценок параметров нормального закона.
- •Выводы.
- •(Необходимая для выполнения работы)
- •Вариант 9
- •Вариант 13
- •Вариант 15
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23.
- •Вариант 24.
Министерство сельского хозяйства РФ, Федеральное агенство по сельскому хозяйству.
ФГОУ ВПО Тюменская государственная сельскохозяйственная академия
Кафедра математики
Методические указания и варианты заданий к контрольной работе №2 по математической статистике
«МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ»
Для студентов технических специальностей
Тюмень - 2010 |
Составитель д.ф.-м.н., профессор Рудаков Б.П
Рецензенты:
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА: Методические указания и варианты заданий по теме: «Математическая обработка экспериментальных данных» для студентов технических специальностей всех форм обучения (2-й курс, 2-й семестр).
Тюмень, Тюменская государственная сельскохозяйственная академия,
2010, С.27.
Методические указания утверждены на заседании кафедры,
Протокол №___________ от «______» _________________ 2010г.
Одобрено
Научно-методическим советом
Института экономики и финансов.
Протокол № _____ от «_______» ____________2010 г.
УТВЕРЖДЕНО УМК академии: протокол № ________ от «________» 2010
РИО ТСХА. Подписано к печати «________». Тираж _____________экз.
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ
ДАННЫХ
( Методические указания к лабораторной работе )
ЗАДАНИЕ. Приведены результаты 50 наблюдений безотказной работы партии электрических лампочек ( в час. работы ):
94 84 73 107 94 107 99 100 104 88
|
129 136 141 88 68 111 110 109 109 106 |
36 47 76 76 77 71 50 49 62 40 |
114 113 123 120 107 118 95 100 96 126 |
98 77 88 94 76 84 125 142 94 84 |
|
Первичная обработка результатов наблюдений.
1).
Выполним группировку данной выборки
случайной величины ( кратко: СВ
X
),
т.е. разобъём наблюдаемые значения
СВ
на к
частичных
интервалов равной длины h
и подсчитаем частоты
 попадания СВ
в частичные интервалы.
попадания СВ
в частичные интервалы.
Просматривая приведённые значения, находим :
 =
36,
=
36,
 =
142.
=
142.
Длину интервала h можно выбирать различными приемами. Одним из удобных при определении h является способ, предложенный Стерджесом:
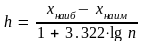 .
.
Здесь n - объём выборки, в нашем задании n = 50. Тогда

За h удобнее взять ближайшее целое число : h = 16.
2). За начало 1-го интервала рекомендуется принять величину,

т.е.
 36
- 8 = 28. Тогда
36
- 8 = 28. Тогда
 28 +
16
= 44,
28 +
16
= 44,
 44
+ 16 = 60 ,
44
+ 16 = 60 ,
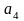 =
76,
=
76,
 =
92,
=
92,
 =
108,
=
108,
 =
124,
=
124,
 =
140,
=
140,
 =156.
=156.
Шкала
интервалов и группировка исходных
статистических данных сведены в
таблицу 1, причем в каждый интервал
включены те значения вариант
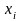 ,
которые удовлетворяют неравенству
,
которые удовлетворяют неравенству
 .
.
Таблица
1
Интервалы ( |
Подсчет частот |
Частоты
|
Относительная частота
|
( 28 ; 44 ] ( 44 ; 60 ] ( 60 ; 76 ] ( 76 ; 92 ] ( 92 ; 108 ] ( 108 ; 124 ] ( 124 ; 140 ] ( 140 ; 156 ]
|
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * |
2 3 7 8 15 9 4 2 |
0,04 0,06 0,14 0,16 0,30 0,18 0,08 0,04 |
К = 8 |
Сумма: |
50 |
1,00 |
3).
Построим дискретный статистический
ряд, найдя середины частичных
интервалов по формуле
 .
Результаты запишем в таблице 2.
.
Результаты запишем в таблице 2.
Таблица 2
Интервалы
|
Середины
|
Частота
|
Относит. Частота
|
Плотность относительной частоты
|
( 28 ; 44 ] ( 44 ; 60 ] ( 60 ; 76 ] ( 76 ; 92 ] ( 92 ; 108 ] ( 108 ; 124 ] ( 124 ; 140 ] ( 140 ; 156 ]
|
36 52 68 84 100 116 132 148 |
2 3 7 8 15 9 4 2 |
0,04 0,06 0,14 0,16 0,30 0,18 0,08 0,04 |
0,00250 0,00375 0,00875 0,01000 0,01875 0,01125 0,00500 0,00250 |
Сумма: |
|
50 |
1,00 |
|
По
данным табл. 2 строим гистограмму.
На оси абсцисс откладываем частичные
интервалы, на каждом из них строим
прямоугольник, площадь которого равна
относительной частоте
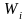 ( для этого за высоту прямоугольника
нужно взять плотность относительной
частоты ). Площадь всех прямоугольников
будет равна единице.
( для этого за высоту прямоугольника
нужно взять плотность относительной
частоты ). Площадь всех прямоугольников
будет равна единице.
Если построена гистограмма интервального распределения, то полигон того же распределения получим, если соединим прямолинейными отрезками середины верхних оснований прямоугольников.


 0,o2
0,o2


 0,01
0,01




 0
28 44 60 76 92 108 124 140
156
0
28 44 60 76 92 108 124 140
156
Рис. 1

 ]
]


