Хід роботи

1. На моделі знайти визначальні елементи симетрії.

2. Для моделей нижчих і середніх сингоній нанести визначальні елементи симетрії на стереографічну проекцію і по ній визначити:

1. загальну просту форму;

2. назву точкової групи;

3. сингонію;

4. всі елементи симетрії даної точкової групи;

5. формулу симетрії.

Дані записати у звіт.

3. На моделі знайти всі елементи симетрії даної точкової групи.

4. Знайти всі прості форми, що є на даній моделі.

5. Схематично (на око) нанести полюсні точки граней знайдених простих форм моделі на стереографічну проекцію. Дати назву простим формам.

6. Остаточні результати заносяться у звіт:

Модель №

Точкова група

Формула симетрії

Сингонія

Назва загальної простої форми

Назви простих форм

Контрольні запитання

1. Яке положення відносно елементів обмеження може займати площина симетрії?

2. Яке положення у кристалах можуть займати осі симетрії?

3. Якого порядку бувають кристалографічні осі?

4. Як визначається центр симетрії кристалографічних моделей?

5. У яких точкових групах симетрії зустрічаються дзеркально-поворотні осі?

6. Чим характеризуються прості форми кристалів?

7. Скільки всього існує різних простих форм кристалів?

8. На чому ґрунтується метод Шубнікова при визначенні класу симетрії?

9. Які Ви знаєте позначення Шубнікова для опису елементів симетрії?

10. Для чого використовується стереографічна проекція?

Лабораторна робота 2 Елементи теоретико-групового аналізу точкових груп

Мета роботи: Засвоїти основні положення теорії групи.

Завдання: Для конкретної точкової групи визначити.

а) порядок групи.

б) побудувати таблицю множення.

в) знайти підгрупи заданої групи.

г) визначити суміжні класи групи по підгрупах.

д) знайти класи спряжених елементів.

е) визначити нормальні ділянки групи.

Об’єкти дослідження: кристалографічні моделі нижчих, середніх та вищих сингоній.

Література: [3], [4], [5]

Теоретичні відомості

Елементи теоретико-групового аналізу точкових груп. Переміщення тіла, яке суміщає його з самим собою, називається перетворенням симетрії. Сукупність всіх перетворень симетрії даного тіла називається його групою симетрії. Вивчення груп симетрії проводиться за допомогою загального математичного апарату теорії груп, деякі положення якої будемо використовувати в цій роботі. Про перетворення симетрії говорять при цьому як про елемент групи.

При всіх перетвореннях симетрії тіла скінчених розмірів принаймні одна точка повинна залишатись нерухомою, ця точка є загальною точкою перетину всіх осей і площин симетрії. В іншому випадку, наприклад, два повороти навколо осей, що не перетинаються, привели би до поступального переміщення тіла, яке уже не суміщає його з самим собою.

Група симетрії, у якій при всіх перетвореннях одна точка лишається нерухомою, називається точковою групою. Група симетрії тіла скінчених розмірів – це точкова група. Вивчення перетворень симетрії є задачею широкого плану. Згідно положень теоретико-групового аналізу точкових груп у першу чергу необхідно ознайомитись з основними поняттями теорії скінчених груп

Приклади груп. Означення групи. Для прикладу розглянемо сукупність із слідуючих шести матриць:

Сукупність Г₃ цих матриць має ту особливість, що добуток довільних двох із них також є матрицею, яка належить до цієї ж сукупності. Множення будь-якої матриці на елемент ε не змінює добуток, а множення матриць σ, λ, μ самих на себе, множення матриць α на матрицю β дають матрицю ε. Така сукупність матриць називається групою. Кожна матриця є елементом групи.

Розглянемо приклад ще більш загального характеру. Нехай задано сукупність σ елементів a, b, c, і т.д. довільної математичної природи так, що при цьому існує закон, згідно з яким для довільних двох однакових або різних елементів а та b можна знайти третій елемент d, який належить до H. Цей закон називається композицією або символічним множенням елементів a та b, а результат цієї дії - добутком елементів a та b.

Виходячи із цих прикладів, можемо дати визначення групи. Сукупність Y елементів називається групою, якщо вона задовольняє наступні постулати:

1. Символічний добуток довільних двох елементів із Y повинен бути елементом Y, тобто, якщо a і b Y, то ab = c Y.

1. Символічне множення асоціативне, тобто для довільних трьох елементів із Y існує співвідношення:

3. Сукупність Y містить одиницю або нейтральний елемент такий, що яким би не був елемент а Є Y, має місце співвідношення:

4. Кожний елемент а Є Y має один і тільки один обернений до себе елемент а , тобто такий, що

В загальному випадку множення елементів групи не комутативне, тобто

Група, множення елементів якої комутативне, тобто добуток довільних елементів не залежить від порядку співмножників, називається абелевою.

Групи, що мають скінчене число елементів називається скінченими, а число елементів q називається порядком групи. Група з нескінченним числом елементів називається нескінченною. Прикладом нескінченної групи можуть бути:

1 Цілі числа (додатні, від’ємні і нуль) відносно додавання, як закону композиції, утворюють групу. Одиницею групи є число нуль, кожному додатному числу відповідає одне від’ємне число як обернений елемент групи.

2. Групою є додатні раціональні числа крім нуля, відносно множення. Одиницею групи є число одиниця.

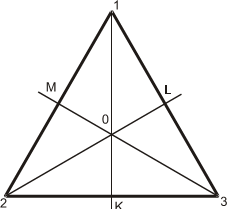
Рис. 2.1. Стереографічна проекція трьохгранної призми.

Таблиця множення елементів групи ( квадрат Келі). Для виконання цілого ряду операцій над елементами групи необхідно знати результат символічного множення будь-яких двох елементів групи. Для цього складається таблиця множення елементів групи.

Створення таблиці розглянемо на конкретному прикладі - для осей симетрії трьохгранної призми (кристалографічна група D₃ або 3:2 ).

Трьохгранна призма має такі осі симетрії. Вісь третього порядку C₃, яка проходить вздовж осі фігури (через точку 0 на .рис.2.1, перпендикулярно до площини рисунка). Три осі другого порядку ( K, L, M рис.2.1), які розміщені перпендикулярно до осі третього порядку.

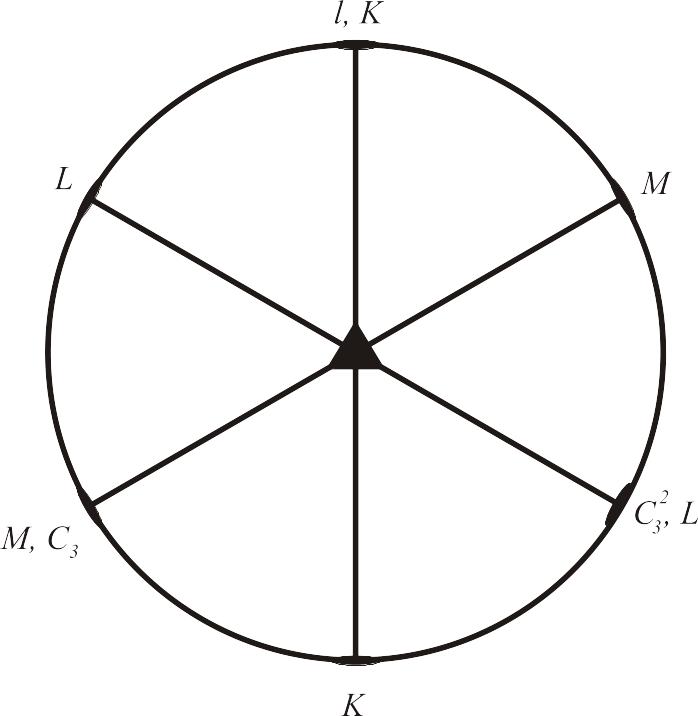
Рис. 2.2. Стереографічна проекція осей призми

Стереографічна проекція всіх осей симетрії даної призми показана на рис.2.2. Сукупність всіх обертань навколо даних осей симетрії буде точковою групою 6-го порядку:

1. Одиничним елементом Е буде поворот навколо осі на кут 0 або 2π.

2. Перший поворот навколо осі С₃ на 120° позначимо як елемент групи С₃.

3. Д

   Рис. 2

   ругий поворот на елементарний кут І20° навколо осі С₃ (відносно вихідного положення це буде кут повороту 240°), позначимо як елемент групи C₃². Таким чином вісь третього порядку до групи D має дати три елементи.

4. Кожна вісь другого порядку в принципі дає два елементи групи: перший поворот на 180° і другий поворот на 180° до суміщення фігури з її вихідним положенням. Остатній поворот буде тотожнім одиночному елементу групи.

Для осей K, L, M, одиничних елементів як елементів групи рахувати не будемо. Оскільки для групової сукупності елементів потрібно лише врахувати один одиничний елемент.

Таким чином, кожна вісь другого порядку дасть по одному елементу групи повороту на 180°. Ці елементи групи позначимо відповідно К, L, М.

Для знаходження таблиці множення елементів групи пропонуємо два методи:

1-й метод.

Позначимо вершини трикутника, який е перпендикулярним до осі C₃ перерізом призми, цифрами 1,2,3 (рис. 2.1). Кожній операції обертання можна співставити відповідну перестановку трьох цих чисел:

У цих позначеннях верхній рядок вказує на вихідне положення фігури, (цифри на рис. 2.1 читаються проти годинникової стрілки), а нижній рядок – на кінцеве положення фігури. Користуючись цим позначенням, можна знайти добуток довільних двох операцій групи. Наприклад,

Практично це виконується так. Після запису позначень елементів, які перемножуються, записують верхній рядок нового елемента. Індекси нижнього рядка заповнюються наступним чином. Перша – цифра нижнього рядка першої дужки (3). Знаходять цю ж цифру у верхньому рядку другого елемента. Цифра, що стоїть під нею у нижньому рядку (у цьому прикладі) і буде результатом множення, тобто її потрібно записати на перше місце в нижній рядок нового елемента. Так само заповнюється друге місце нижнього рядка і т.д.

Таблиця 2.1. Таблиця множення елементів

D3 E K L M E E K L M E M K L E L M K K K L M E L L M K E M M K L E

Обчислюючи всі можливі добутки елементів групи D₃, знайдемо таблицю множення ІІ. Таблиця множення повністю характеризує групу.

2-й метод.

Цей метод побудови таблиці множення не потребує жодних спеціальних позначень елементів групи, що мало місце в першому методі. Даний метод базується на використанні стереографічної проекції всіх елементів симетрії даної групи (рис.2.2). Навколо стереографічної проекції записуються позначення елементів групи, які створюються відповідними елементами симетрії. Наприклад, зверху стереографічної проекції наносимо одиничний елемент l (рис.2.2). При повороті (в напрямку руху проти годинникової стрілки) на кут 120° фіксуємо елемент групи , при повороті ще на 120° фіксуємо елемент

Оскільки осі другого порядку лежать в площині стереографічної проекції, то для зручності, елементи, які вони відображають, записуємо біля обох кінців осі. Наприклад, K↔L, L↔L, M↔M

Наносимо на стереографічну проекцію одну лише довільну полюсну точку.

Якщо потрібно одержати результат символічного множення довільних двох елементів, то спочатку діємо першим елементом на цю полюсну точку, а потім продовжуємо діяти другим елементом. Одержаний результат – полюсна точка –співставляється з вихідною полюсною точною з метою знаходження елемента групи, який би сам виконав тотожну операцію. Результатом множення і буде цей елемент.

Наприклад, «множимо» два елементи , L. Елемент полюсну точку переведе в положення нижче лінії MM (рис.2.2). Для цієї точки залишається позначення «О». Діючи віссю LL на цю точку, переведемо її в верхню частину проекції (справа від лінії КК). В результаті цієї операції полюсна точка буде мати позначення «х» і розміститься симетрично вихідній точці відносно лінії КК. Це вказує на те, що дану вихідну полюсну точку можна сумістити з отриманою точкою шляхом повороту її навколо осі К, тобто маємо L = K.

Підгрупа. Якщо із групи Р можна виділити таку сукупність елементів Н, яка сама буде групою відносно цієї самої групової дії, то сукупність елементів H називається підгрупою групи Р

Прикладом підгрупи D₃ є сукупність елементів, , , які відносно групової дії – обертання – утворюють групу Група є абелевою підгрупою групи D.

Зауважимо, що група утворюється степенями одного і того ж елемента ( )²= ,( )³ = l

Такі групи називаються циклічними.

Суміжні класи. Нехай rpyпa Р порядку р містить підгрупу Н порядку h. Очевидно, що h < p. Елементи підгрупи Н позначимо символами h_i; де і = 2,3,…, h_n. h_i = E. Елементи групи Р, які не входять до підгрупи Н, позначимо символами р_j, де j = 2,3.

Помножимо кожний елемент підгрупи Н справа на елемент Р₂, тоді сукупність НР_2:

(2.1)

називається правим суміжним класом групи Р по підгрупі Н.

Теорема 1. Суміжний клас НР₂ не перетинається з підгрупою Н, тобто не має з нею спільних елементів.

Дійсно, нехай (2.2)

Помножимо рівність (2) на обернений елемент :

Тоді, Н, але Р₂ не входить до підгрупи н умовою. Отже,

Теорема доведена.

Разом з підгрупою Н суміжний клас НР₂ містить 2h різних елементів групи Р. Якщо, p > 2h, то виберемо елемент р₃ Р такий, що не входить ні до Н, ні до НР₂ і утворимо ще один правий суміжник клас НР₃:

(2.3)

Теорема 2. Суміжні класи не перетинаються між собою. Припустимо, що

. (2.4)

Помножимо рівність (2.4) на :

.

Звідси: ,

тобто, цим доведенням показано, що елемент належить до суміжного класу НР₂, а це суперечить умові вибору елемента р₃. Таким чином, суміжні класи, дійсно не мають спільних елементів.

Якщо Р = hj, то розклад групи на суміжні класи по даній підгрупі припиняється і в цілому можна записати цей розклад:

, (2.5)

де j - число суміжних класів (включаючи і підгрупу) по підгрупі, і називається індексом підгрупи.

Теорема Лагранта: Із .розкладу (5) безпосередньо випливає теорема Лагранта: порядок h та індекс j підгрупи є дільниками порядку Р групи.

P = hj (2.6)

З допомогою теореми Лагранта можна встановити порядки можливих підгруп, якщо відомий порядок групи. Якщо порядок групи є простим числом, то воно не має жодних підгруп, крім тривіальної, що складається з одиниці.

Приклад: Група D₃ має тільки один суміжний клас по підгрупі С₃:

C₃K = {K,L,M}

Класи спряжених елементів. Два елементи а та b групи Р називаються спряженими, якщо існує хоча би один елемент с   Р такий , що

(2.7)

Кажуть, що елемент b є перетворенням елемента а з допомогою с, а саме перетворення називається перетворенням подібності.

Сукупність елементів групи, що утворюється шляхом перетворення подібності (2.7) елемента а, де с пробігає всі елементи групи, називається класом спряжених елементів, або класом елемента а

Одиниця групи l утворює клас, тому що для довільного елемента с Р.

В абелевих групах кожен клас складається з одного елемента.

Кожна скінчена група розкладається па скінчене число класів спряжених елементів:

(2.8)

Для прикладу знайдемо клас елемента групи D₃.

Таким чином, до класу елемента входить два елементи групи: та . Позначимо цей клас символом . Перший клас утворюється одиницею: . Подібним чином можна знайти третій клас групи D_3.

Отже в групі D₃ є три класи спряжених елементів

.

Число елементів групи в класі називають порядком класу.

Наприклад: порядок К₂ є 2, порядок К₃ є 3.

Тут лише потрібно пам’ятати , що крім поняття «порядок класу» існує ще поняття порядок елемента групи.

Порядок елемента групи визначається із умови аⁿ = Е, де n - порядок елемента.

Всі елементи одного і того ж класу мають однаковий порядок. Наприклад, елементи , є D₃ мають третій порядок.

Нормальний дільник. Підгрупа N групи P , що складається тільки з цілих класів спряжених елементів, називається інваріантною підгрупою або нормальним дільником.

Групи, які не мають нормальних дільників, називаються простими. Якщо група містить хоч би один відмінний від одиниці нормальний дільник, то вона називається складною. Група називається напівпростою, якщо одна з її інваріантних підгруп не є абелевою.