3. Обработка результатов косвенных измерений
Большинство физических величин обычно нельзя измерить непосредственно, и их определение состоит из двух этапов – прямые измерения одной (x) величины или более (x, у, z, …) и последующий расчет искомой величины f по формуле: f = f(x, у, z, …).
Следовательно, и оценка погрешностей также включает в себя два этапа. Сначала необходимо оценить погрешность каждой из величин x, у, z, …, которые измеряются непосредственно в ходе прямых измерений, а затем определить, как эти погрешности (x, у, z, …) влияют на погрешность конечного результата, т. е. найти f.
Отметим, что среди величин x, у, z, … могут содержаться не только не-посредственно измеряемые величины, но и табличные (значения которых в данном опыте не измеряются, а берутся из таблиц) и так называемые данные установки (некоторые известные ранее характеристики экспериментальной установки, не измеряемые в данном опыте).
Способ оценки погрешностей таких величин изложен в прил. 3.
3.1. Расчет погрешности при косвенных измерениях
Пусть в результате обработки всех непосредственно измеряемых величин x, у, z, … для каждой из них найдены средние значения <x>, <у>, <z>, …, погрешности абсолютные x, у, z, … и относительные x, y, z, … .
Требуется найти среднее значение <f> искомой величины, а также абсолютную f и относительную f погрешности.
Среднее значение <f > вычисляют при средних значениях величин x, у, z, …, от которых зависит измеряемая величина f, путем их подстановки в расчетную формулу:
< f > = f (<x>, <y>, <z>, …). (11)
Если прямые измерения величин x, у, z, … выполняются независимо и подвержены только случайным погрешностям, то абсолютная погрешность f косвенно измеряемой величины f определяется следующим образом:
,
(12)
где
частные производные
,
,
,
… вычисляются при средних значениях
<x>,
<у>,
<z>,
…, а количество слагаемых в сумме
определяется числом величин, абсолютные
погрешности которых найдены (подробнее
о частных производных см. в прил. 4).
Из формулы (12) следует, что влияние составляющей абсолютной пог-решности быстро падает по мере уменьшения этой составляющей.
Поэтому
при вычислении абсолютной погрешности
косвенного измерения целесообразно
сначала вычислить все ее составляющие
, 
,
,
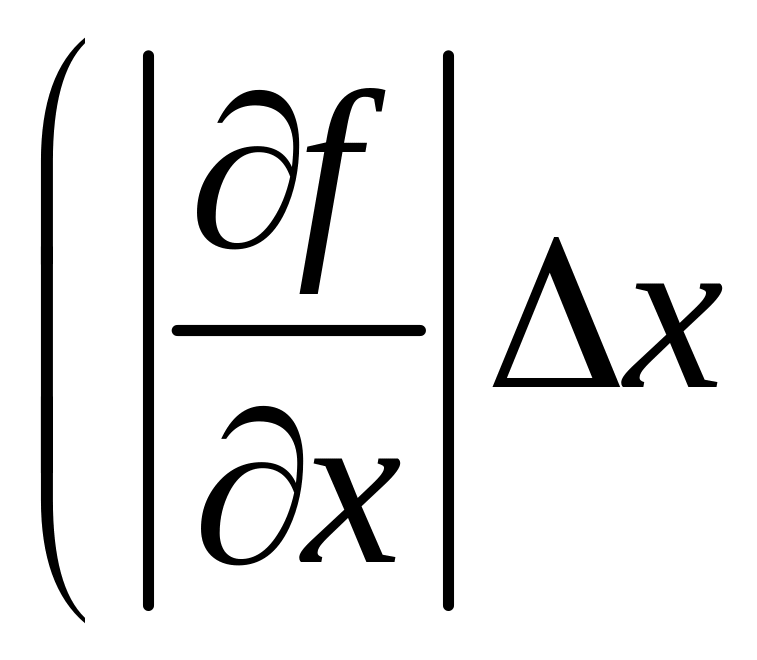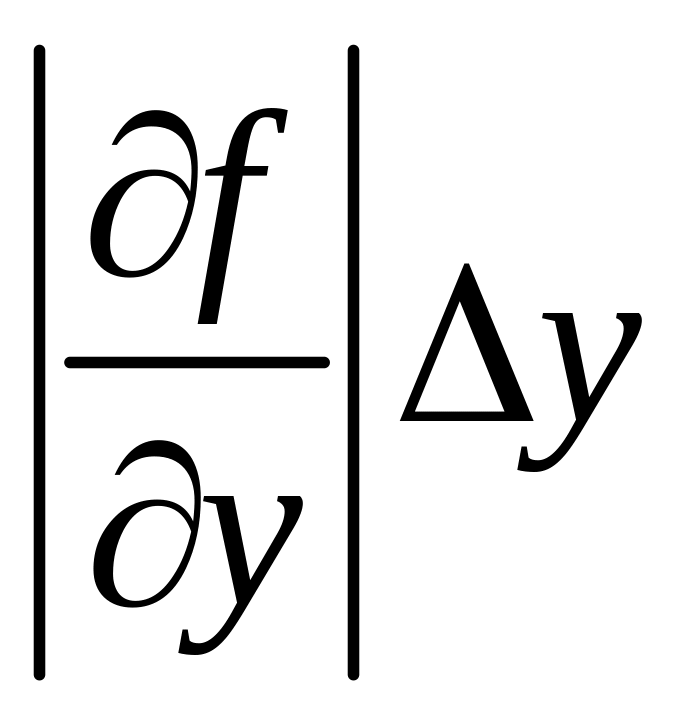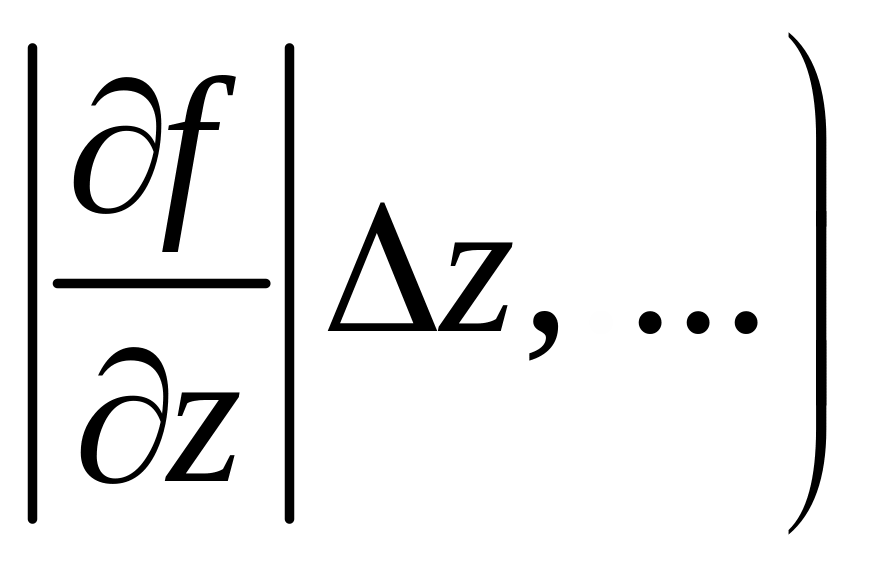сравнить их и затем пренебречь теми,
которые меньше максимальной в несколько
раз. Кроме
того, сравнивая значения составляющих
погрешностей, можно выявить значение
прямого измерения, которое в наибольшей
степени влияет на общую погрешность.
При необходимости точность результата
этого измерения можно увеличить в целях
повышения точности эксперимента в
целом.
Относительная погрешность косвенно измеряемой величины f вычисляется известным способом:
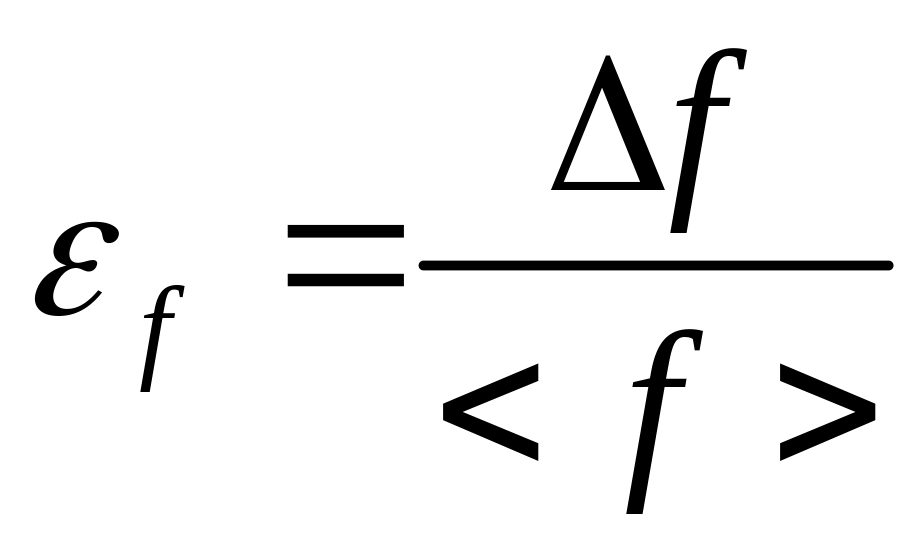100
%. (13)
Затем округляют результаты расчета и записывают окончательный результат измерения в стандартном виде:
f = ( < f > f) ед. изм. с f = … %. (14)
Если искомая величина представляет собой выражение вида
f = f(x, y, z) = xaybzc, (15)
т. е. не содержит операций сложения и вычитания, причем постоянные a, b, c могут принимать как положительные, так и отрицательные значения, проще сначала найти относительную погрешность f. Действительно,
=
=
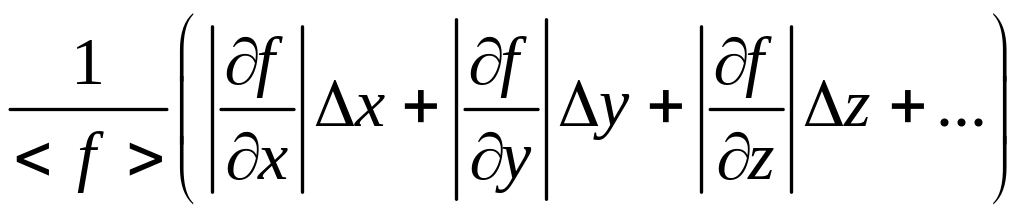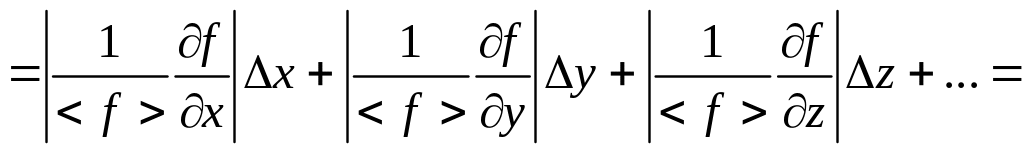
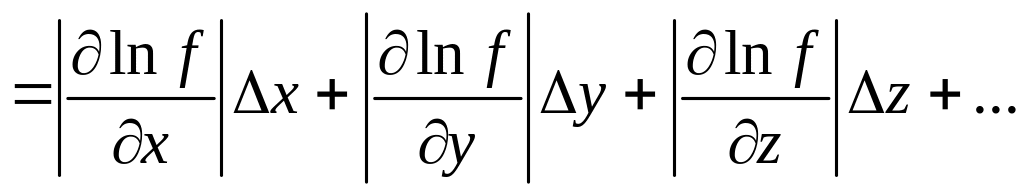(16)
Прологарифмируем выражение (15):
ln f = aln x + bln y + cln z. (17)
Вычисляя частные производные, получим:
;
;
.
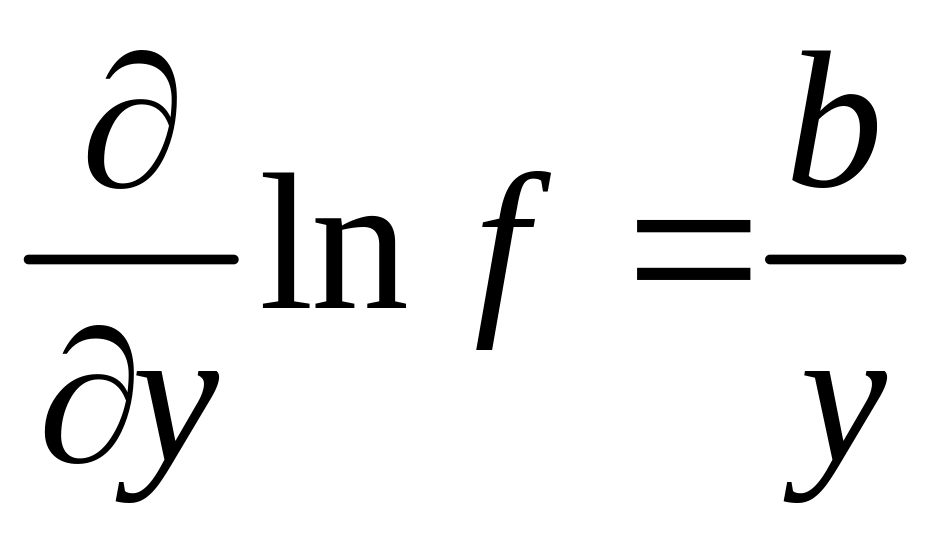(18)
Окончательно формула для нахождения относительной погрешности примет вид:
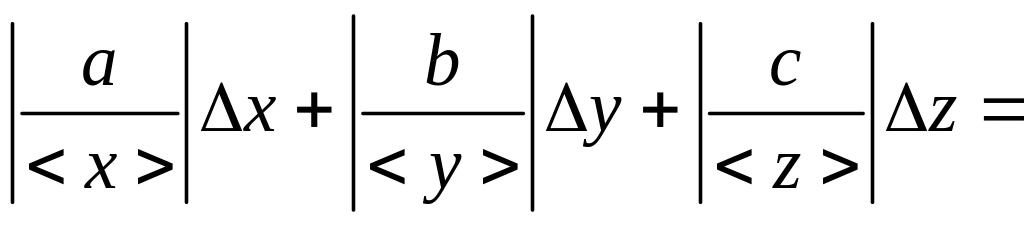ax
+ by
+ cz.
(19)
После этого рассчитывают абсолютную погрешность f по формуле: f = f<f> и записывают окончательный результат в виде формулы (14).