3.2. Расчет погрешности при косвенных измерениях, если условия эксперимента невоспроизводимы

Рассмотрим расчет погрешности при косвенных измерениях, если практически невозможно воспроизвести прежние условия проведения эксперимента. В этом случае после проведения многократных прямых измерений величин x, у, z, … для получения окончательного результата, т. е. <f>, f, _f , необходимо выполнить действия в следующем порядке:

1) для каждого из значений x_i, у_i, z_i, … вычислить значение f_i косвенно определяемой величины:

f_i = f(x_i, y_i, z_i, …); (20)

2) определить среднее значение измеряемой величины:

<f> 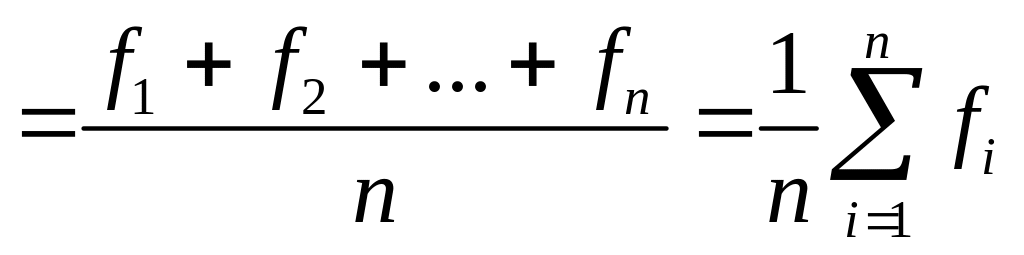; (21)

3) вычислить погрешность каждого измерения:

f_i = <f>  f_i, i = 1, …, n; (22)

4) рассчитать случайную погрешность измерений:

f_сл 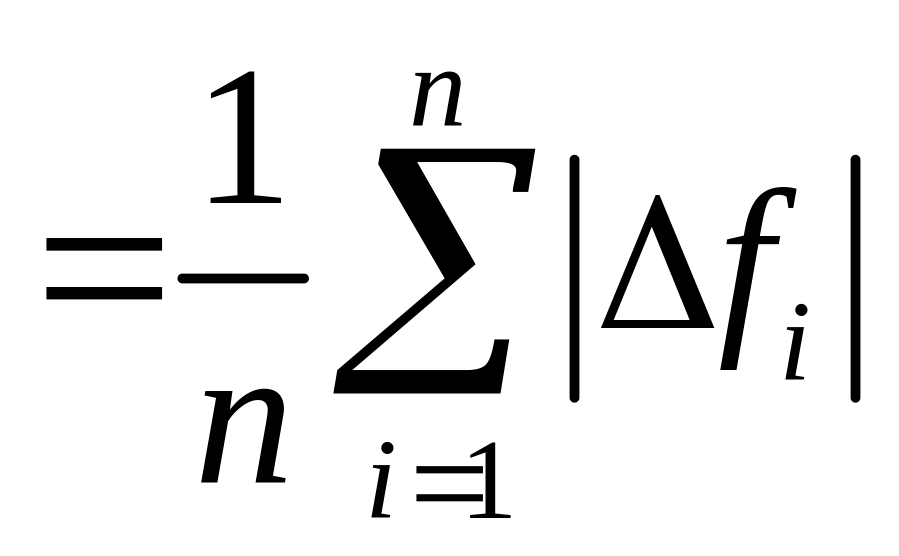; (23)

5) вычислить погрешность, вносимую различными инструментами в абсолютную погрешность косвенно измеряемой величины (назовем формально эту погрешность инструментальной f_ин):

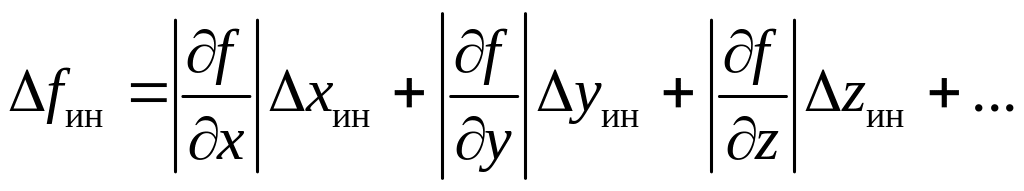. (24)

При этом после нахождения частных производных в полученное выражение следует подставить наименьшие из измеренных значений x, у, z, …, приводящие к наибольшей погрешности f_ин;

6) определить абсолютную погрешность:

f = f_сл + f_ин; (25)

7) рассчитать относительную погрешность:

100 %; (26)

8) произведя округление результатов расчета, записать окончательный результат измерения в виде:

f = (<f>  f) ед. изм. с _f = … %. (27)

4. Пример измерения и расчета погрешности

Цель измерения: рассчитать плотность твердого тела цилиндрической формы.

По определению плотность тела   это масса единицы объема вещества,

 = , (28)

поэтому достаточно прямыми методами измерить массу m тела (взвесить на весах) и объем V тела (например, погружая тело в мензурку с водой) и вычислить плотность по формуле. Однако будем считать, что нет возможности прямыми методами измерить объем тела (нет подходящей мензурки). тогда объем цилиндра можно вычислить по формуле:

V = , (29)

где d и h  диаметр основания и высота цилиндра.

Рабочая формула (28) для расчета плотности твердого тела цилиндрической формы примет вид:

 = , (30)

отсюда видно, что необходимы прямые измерения массы m, диаметра d и высоты h цилиндра. Предположим, что оценочные измерения дали следующие результаты: m  50 г; d  12 мм; h  50 мм. Чтобы относительная погрешность каждого измерения не превышала, например, 0,5 %, необходимы измерительные инструменты с наименьшей ценой деления: соответственно m_ин  0,25 г; d_ин  0,06 мм; h_ин  0,25 мм.

В лаборатории имеются весы с наименьшей ценой деления (наименьшим имеющимся разновеском) в 10 мг, что позволяет провести измерение массы с относительной погрешностью 0,02 %.

Измерение высоты проведем штангенциркулем с наименьшей ценой деления 0,1 мм, при этом относительная погрешность будет равна 0,2 %. Для измерения диаметра используем микрометр с наименьшей ценой деления 0,01 мм, что даст относительную погрешность 0,1 %.

1) Проведем прямые измерения.

Масса цилиндра

m = (49,32  0,01) г с _m = 0,020 %. (31)

Измерения штангенциркулем высоты цилиндра в пяти различных местах в пределах инструментальной погрешности в 0,1 мм не обнаружили непараллельности оснований цилиндра (это указывает на малые случайные погреш-ности h_cл < h_ин).

Результат измерения запишем в виде:

h = (52,6  0,1) мм с _h = 0,19 %. (32)

При измерении диаметра цилиндра d, мм, микрометром с ценой деления в 0,01 мм в пяти положениях, различных по высоте и периметру цилиндра, получили следующие значения: 12,33; 12,36; 12,37; 12,34; 12,37.

Проведем математическую обработку результатов прямых измерений диаметра цилиндра:

а) среднее арифметическое значение диаметра

<d> = = 12,354 мм; (33)

б) абсолютная погрешность многократных измерений диаметра

d =  =

= 0,0252 мм  0,025 мм; (34)

в) относительная погрешность измерений _d = (0,025/12,354)100 % = 0,20 %;

г) окончательный результат измерения диаметра цилиндра записывается в виде:

d = (12,354  0,025) мм с _d = 0,20 %. (35)

Число  = 3,14  0,005 с _ = 0,16 % (в соответствии с прил. 3).

2) Приступаем к вычислениям плотности материала и ее погрешности. Действительное значение плотности подсчитаем по формуле (30):

<> кг/м³. (36)

3) Поскольку формула для расчета плотности может быть записана в виде произведения

 = 4m^1d^2h^1,

проще сначала найти относительную погрешность _:

а) прологарифмируем выражение (30):

ln  = ln 4 + ln m – ln   2 ln d – ln h; (37)

б) найдем частные производные от ln  по каждой измеренной величине:

(38)

в) согласно выражению (16) формула для расчета относительной погрешности примет вид:

_ = + + + ; (39)

г) расчет относительной погрешности даст результат:

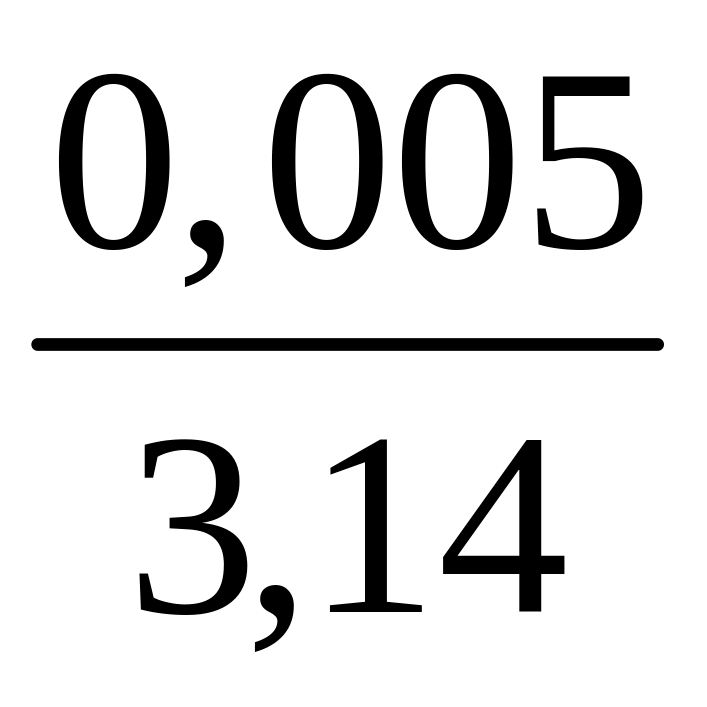_ = + + + = 0,0086 или 0,86 %. (40)

4) Абсолютная погрешность результата

 = 7831,20,0086 = 67,348  67 кг/м³. (41)

5) Окончательный результат измерения плотности материала запишем в виде:

 = (7,831  0,067)10³ кг/м³ с _  0,86 %. (42)

Полученное значение плотности в пределах погрешности измерений соответствует плотности железа (_табл = 7,810³ кг/м³).