9.1.4. Подвійний векторний добуток трьох векторів

Він дається виразом:

. (9.10)

Геометрично вектор перпендикулярний до площини, в якій лежать вектори та .

9.2. Поняття функції багатьох змінних. Частинні похідні. Повний диференціал. Градієнт скалярної функції багатьох змінних

У багатьох задачах фізики маємо справу із змінними величинами, значення яких повністю визначають певним набором інших змінних величин. Наприклад, швидкість матеріальної точки під час її руху під дією сили залежить від координат і часу: , а під час розгляду нестаціонарного руху рідини швидкість частинок рідини також була функцією координати і часу . Подібні функціональні залежності, в яких деяка змінна величина є функцією певної кількості незалежних змінних величин, називають функціями багатьох змінних.

Розглянемо функцію , визначену в деякому околі точки . Зафіксуємо змінні та . Внаслідок отримаємо функцію , залежну лише від однієї змінної. Якщо ця функція має похідну за змінною , то цю похідну назвемо частинною похідною функції :

.

Величину називають частинним приростом функції за зміною у точці . Подібно можна знайти та . Отриманий результат справедливий не лише для точки ), але і для довільної точки . Пам’ятаємо лише, що частинну похідну беруть згідно з правилами диференціювання функції однієї змінної.

Приріст функції , обумовлений змінами та на та може бути записаний у вигляді:

(9.11)

Вираз (9.11) є повним диференціалом функції . Відзначимо, що повний диференціал може мати лише функція, диференційовна в точці . Вираз (9.11) дає лінійні стосовно та прирости функції .

Якщо сукупність змінних вважати складовими деякого вектора , то у тривимірному просторі повний диференціал можна виразити як скалярний добуток вектора на вектор :

(9.12)

Таким чином

= ,

або: (9.13)

Тут – диференціальний оператор Набла:

= . (9.14)

Вираз (9.13) показує операцію знаходження градієнта функції . Напрям вектора дає напрямок найшвидшої зміни функції .

9.3. Комплексні числа та їх використання під час розгляду коливних і хвильових процесів

Положення точки на площині задаємо комплексним числом

(9.15)

– модуль комплексного числа,

Я кщо використати формулу Ейлера:

, (9. 16)

то

Нехай – радіус-вектор матеріальної точки, що обертається по колу з кутовою швидкістю , тоді

,

де початкова фаза руху.

Якщо взяти дійсну частину виразу, то отримаємо рівняння гармонійних коливань вздовж осі :

(9.17)

Для опису коливань вздовж осі шукаємо уявну частину виразу

(9.18)

Вирази типу (9.17), (9.18) зручно використовувати для опису коливних та хвильових процесів. Зокрема, вираз:

(9.19)

є рівнянням гармонійного коливання, а вираз

(9.20)

є рівнянням плоскої хвилі.

Використання комплексних чисел для опису коливних та хвильових процесів дає змогу у ряді задач спростити і скоротити розрахунки. Покажемо це на прикладі вимушених коливань.

Виходимо із рівняння руху (7.50) для вимушених коливань, в якому вираз для вимушуючої сили замінимо виразом :

(9.21)

Розв’язок рівняння для встановлених коливань шукаємо у вигляді

, (9.22)

де – деяка стаціонарна незалежна від часу амплітуда у вигляді комплексного числа. Підстановка виразу (9.22) у рівняння (9.21) дає наступний результат:

.

Скоротивши вираз на для отримаємо:

(9.23)

Перетворимо знаменник у виразі (9.23), використавши формулу Ейлера, до вигляду:

,

де , тому .

Кінцево розв’язок рівняння (9. 21) набуває вигляду:

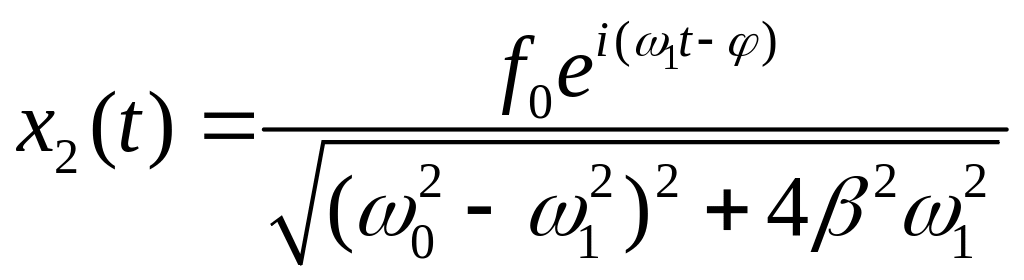(9.24)

З (9.24) видно, що вимушене коливання за фазою відстає від вимушуючої сили на кут . Отриманий результат ідентичний виразу (7.53).

1 Доведемо, що .

Згідно з третім законом Ньютона , а тому для доведення записаної вище рівності достатньо показати, що . Запишемо , де –вектор, що з’єднує точки та , тоді:

, бо , внаслідок колінеарності векторів та .

2 Дане твердження випливає з того, що кут малий ( ), а тому і трикутник AOC рівнобедрений з рівними сторонами .

3 Відзначимо, що середні значення функції та за період рівні 1/2: .

4

5 Адіабатичний процес – процес, що відбувається без обміну теплом із зовнішнім середовищем. Ідеальних адіабатичних процесів в природі немає. Адіабатичними процесами можуть вважатись лише швидкозмінні процеси (в даному випадку пружні деформації в хвилі).

138