7.4.2. Додавання взаємно перпендикулярних коливань

Розглянемо рух матеріальної точки, яка одночасно приймає участь у декількох коливних рухах в різних напрямах. Найпростішою задачею даного плану є задача додавання двох взаємно перпендикулярних коливань однакової частоти

.

Нехай матеріальна точка одночасно виконує коливання: і , . Знайдемо рівняння траєкторії результуючого руху. Для цього з обох рівнянь виключимо час і знайдемо взаємозв’язок між і .

; (7.26)

Врахуємо, що , а і підставимо їх у вираз ( 7.26):

Після перетворення останнього виразу отримаємо:

(7.27)

В ираз (7.27) є рівнянням еліпса, орієнтованого до-вільно відносно осей та . Дослідимо форму траєкторії в декількох часткових випадках:

а) За умови , рівняння (7.27) набуває вигляду:

(7.28)

Вираз (7.28) є рівнянням еліпса, півосі якого співпадають з осями і . Див. рис. 41.

Коли математичний маят-ник одночасно виконує коливання в напрямах і , то матеріальна точка, що є складовою маятника рухається траєкторією, зображеною на рис. 41. У випадку рівності амплітуд , еліптична траєкторія руху вироджується в коло.

б) За умови ; вираз (7.27)набуває вигляду:

(7.29)

З цього виразу отримаємо (див. рис. 42). Це рівняння прямої. Матеріальна точка рухається вздовж прямої з кутовим коефіцієнтом . Її максимальне відхилення в напрямі цієї прямої .

Рівняння коливання точки вздовж прямої

.

в) За умови вираз (7.27) набуває вигляду:

або (див. рис. 43). (7.30)

Результуючим рухом буде коливний рух вздовж прямої з кутовим коефі-цієнтом .

Якщо відміннй від 0, ; та , то траєкторією руху буде еліпс, орієнтація якого відносно і визначається кутом .

У процесі додавання взаємно перпендикулярних коливань з різними частотами результуючими траєкторіями є криві складних форм, які називають фігурами Лісажу. Вигляд цих кривих суттєво залежить як від співвідношення між частотами коливань так і від початкової різниці фаз коливань.

Відносно прості фігури Лісажу отримуються під час додавання коливань, частоти яких кратні. Для прикладу на рис. 44 показані фігури Лісажу, що отримуються у разі додавання коливань з різними відношеннями частот і різною різницею початкових фаз коливань.

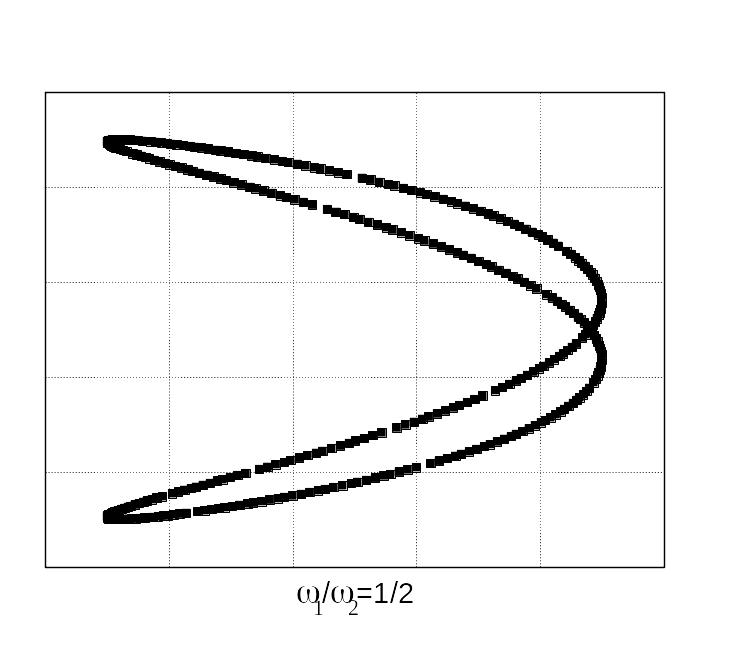
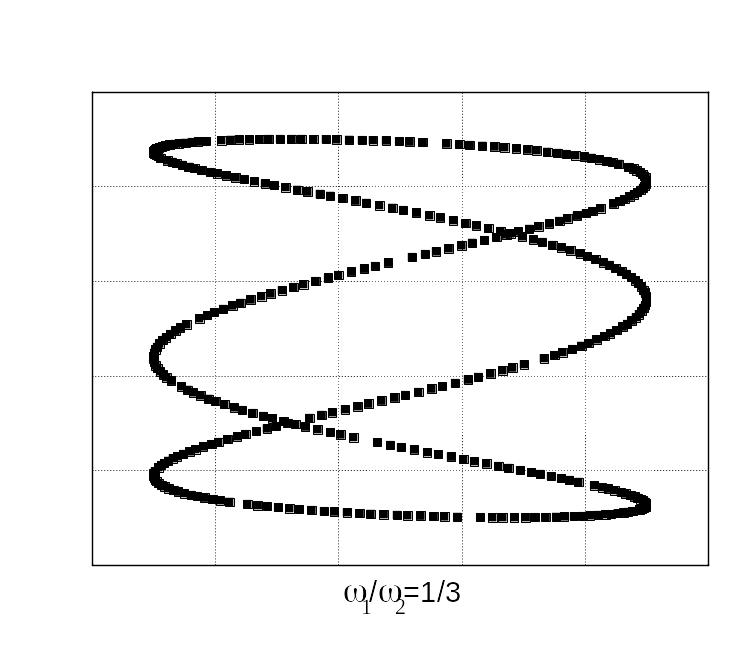
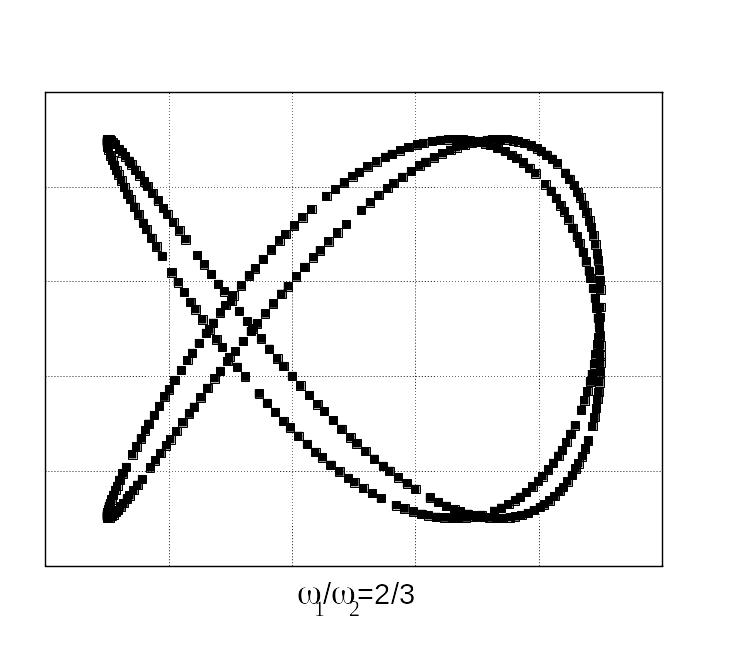
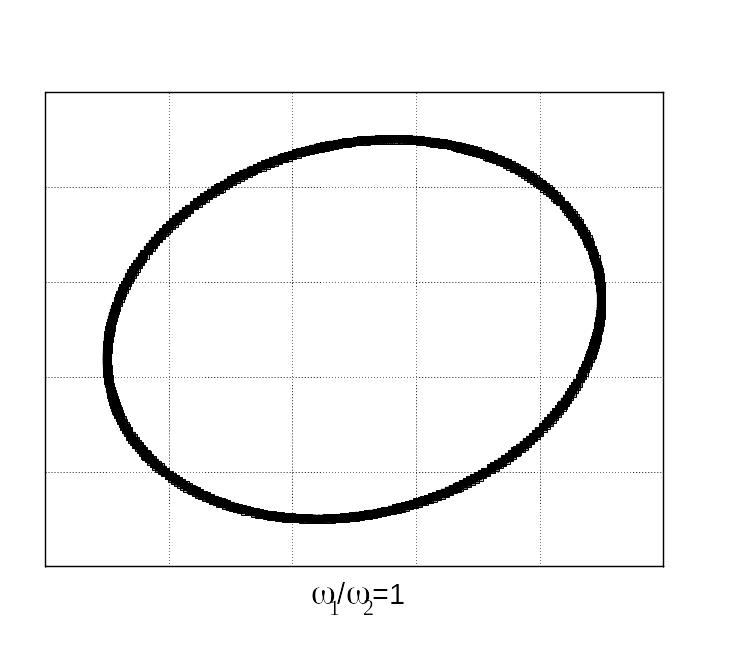
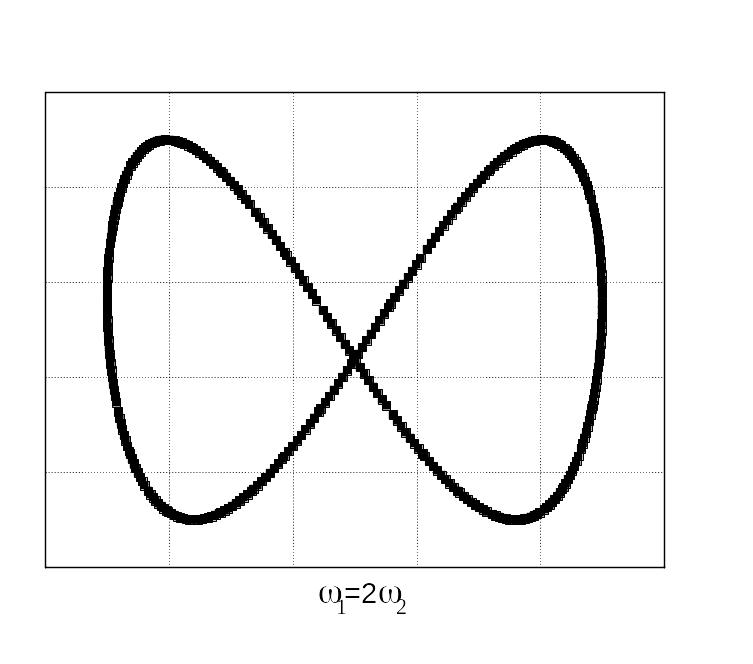
7.5. Коливання за наявності сил опору середовища. Згасаючі коливання та їх характеристики.

У реальних коливних системах завжди діють сили тертя і опору середовища. За цих умов мають місце втрати енергії на подолання цих сил, а також на збудження коливань у навколишньому середовищі. Усе це призводить до зменшення енергії коливань, що проявляється у зменшенні амплітуди коливань, оскільки енергія коливання пропорційна до квадрата амплітуди: . Коливання, які відбуваються з поступовою втратою їхньої енергії називаються згасаючими.

Під час розгляду коливних процесів у попередніх параграфах використовувались припущення про невеликі відхилення систем від положення рівноваги. Тому, під час аналізу впливу сил тертя на коливні процеси, з достатньою точністю можна вважати, що дані процеси відбуваються з малими швидкостями і величина сили опору (тертя) пропорційна до швидкості руху:

(7.31)

З урахуванням сили тертя рівняння руху одномірної коливної системи набуває вигляду

, (7.32)

або

Ввівши позначення та , отримаємо:

(7.33)

Розв’язок рівняння (7.33) шукатимемо у вигляді:

(7.34)

Вважаємо, що вплив сил тертя призводить до зменшення амплітуди коливань з часом: . Підставивши (7.34) у (7.33), отримаємо⁴:

(7.35)

Вираз (7.35) тотожно дорівнює нулеві, коли коефіцієнти при та дорівнюють нулю. Тому:

(7.36)

(7.37)

Оскільки , то розв’язок рівняння (7.37) зводиться до наступного: , або .

Проінтегруємо останній вираз і отримаємо:

, або .

Сталу інтегрування знайдемо з початкових умов. Нехай при амплітуда коливань дорівнює , тоді і

(7.39)

З виразу (7.39) видно, що амплітуда коливань за наявності опору середовища зменшується за експоненціальним законом.

Підставимо (7.39) у рівняння (7.36) і отримаємо:

+( =0

Скоротивши вираз на , знайдемо невідому величину :

, або

(7.40)

Кінцево розв’язок рівняння (7.33) набуває вигляду (рис. 45):

(7.41)

Таким чином, частота коливань системи за наявності опору середовища менша від частоти коливань системи без втрат. Це зменшення частоти тим більше, чим більший коефіцієнт, що характеризує опір середовища: і . Зокрема, у разі значних сил тертя, коли , з виразу (7.40) отримуємо уявне значення . Це свідчить про те, що у системі відсутні періодичні коливні рухи, а є лише неперіодичне повернення системи до положення рівноваги (рис. 46).

Характеристики згасаючих коливань.

1. Коефіцієнт згасання – це величина, обернена до часу , впродовж якого амплітуда коливання зменшиться в разів:

(7.42)

2. Декремент згасання – відношення двох послідовних амплітуд:

(7.43)

3. Логарифмічний декремент згасання:

(7.44)

Величина обернена до дорівнює кількості коливань, протягом яких амплітуда коливань зменшиться в разів:

(7.45)

4. Добротність коливної системи:

. (7.46)

Добротність характеризує енергетичні втрати системи за один період.

Відомо, що енергія коливної системи пропорційна до квадрату амплітуди. Тому закон зменшення енергії коливань можна записати:

, (7.47)

де – енергія коливання при . Швидкість зміни енергії з часом дорівнює . Тоді, продиференціювавши (7.47), отримаємо

.

Якщо згасання коливань мале, то зміна енергії коливань за період приблизно дорівнює:

, або

(7.48)

Тобто, у разі незначного згасання, добротність системи з точністю до множника дорівнює відношенню енергії коливної системи на даний момент часу до втрати енергії за один період.