6.3. Рух в’язкої рідини. Ламінарна і турбулентна течія. Формула Пуазейля.

У реальній рідині під час руху одних шарів відносно інших виникають сили в’язкого тертя. Експериментально встановлено, що сили внутрішнього тертя між двома шарами рідини, що рухаються з різними швидкостями і , можна описати за допомогою формули:

, (6.9)

У виразі (6.9) – площа шарів, що взаємодіють, – відстань між шарами,

– динамічна в’язкість рідини (коефіцієнт пропорційності, залежний від сорту рідини, її стану, зокрема температури). Більш точніше дана залежність описується формулою Ньютона (див. вираз (3.7)):

.

В’язкість рідини чисельно дорівнює силі тертя між двома шарами площею =1 при одиничному градієнті швидкості =1. Розмірність в’язкості .

У багатьох задачах використовують величину – коефіцієнт кінематичної в’язкості ( – густина рідини).

Розглядаючи рух рідини розрізняють два крайні типи течії рідини – ламінарну та турбулентну.

У ламінарній течії окремі шари рідини не змішуються між собою, ковзаючи один відносно одного. Ламінарна течія є стаціонарною.

Із збільшенням швидкості течії рідини ламінарна течія стає нестійкою і переходить у турбулентну. Під час турбулентного потоку частинки рідини рухаються складними траєкторіями, утворюючи вихори із замкненими траєкторіями, рідина інтенсивно перемішується.

Умови переходу від ламінарної до турбулентної течії характеризують числом Рейнольдса:

, (6.10)

у якому – характерний поперечний розмір тіла, що взаємодіє з рідиною. Для передбачення характеру руху рідини в конкретних задачах використовують розрахунок числа Рейнольдса. За малих величин простежується ламінарна течія рідини. Починаючи з якогось критичного значення числа Рейнольдса течія рідини набуває турбулентного характеру.

Зокрема, для води, що тече гладкою циліндричною трубою круглого перерізу діаметром . критичне число Рейнольдса дорівнює :

, (6.11)

де – середня швидкість течії рідини. Для води в трубі діаметром 0,02 м при середня швидкість, при якій число Рейнольдса досягає критичного значення, дорівнює 0,2 м/с.

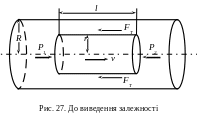Проаналізуємо детальніше стаціонарну течію рідини в розміщеній горизонтально однорідній циліндричній трубі радіуса . Знайдемо закон зміни швидкості рідини з відстанню від осі труби ( ) до її стінок ( ). Уявно виділимо у рідині циліндричний об’єм радіуса і довжиною , вісь якого співпадає з віссю труби (рис. 27).

За умови стаціонарної течії рідини сумарна сила тиску зрівноважується силою тертя , де – площа бічної поверхні вибраного циліндра, – площа основи циліндра, – перепад тиску між основами циліндра, – градієнт швидкості. Запишемо цю умову у вигляді рівняння і знайдемо з нього :

(6.12)

.

Оскільки швидкість рідини біля стінок дорівнює нулю ( при ), то

.

Отже:

. (6.13)

Якщо вважати, що швидкість рідини на осі труби , то вираз (6.13) можна записати у вигляді:

(6.14)

З виразу (6.14) видно, що залежність параболічна (рис. 28).

Вираз (6.13) можна використати для розрахунку об’єму рідини, що протікає через поперечний переріз труби за одиницю часу. Для цього поперечний переріз труби розіб’ємо на концентричні кільця радіуса товщини (рис. 29). Площа кільця дорівнює . За одиницю часу через поперечний переріз кільця протікає об’єм рідини , який дорівнює:

(6.15)

Знайдемо суму об’ємів рідини, яка пройшла за одиницю часу через повний поперечний переріз труби:

(6.16)

В ираз (6.16) називають формулою Пуазейля. За допомогою цього виразу знаходять кількість (об’єм) рідини, що протікає через поперечний переріз круглої труби радіуса за одиницю часу. З виразу видно, що , а тому збільшення радіуса труби у два рази дозволяє збільшити пропускну здатність труби у 16 разів. Вираз (6.16) справедливий лише для ламінарної течії рідини.