6. Механіка рідин

Відміна властивостей рідин і газів від властивостей твердих тіл полягає у відсутності в них пружності, форми і у відсутності опору під час деформації зсуву. Їм властива лише пружність об’єму. Тому в рідині або газі існує лише пружна деформація стиску. Внаслідок цього у стані рівноваги в них існують напруження, перпендикулярні до поверхні, на яку вони діють. Закони механіки, що описують властивості рідин і газів, подібні між собою, а тому будемо говорити про рідину, пам’ятаючи, що отримані висновки справедливі і для газів. Рухливість частинок рідин і газів відносно велика, а під час руху елементи їх мас змінюють своє взаємне розташування.

Механіка рідин складається з двох основних розділів:

1. Гідростатика – вивчає умови рівноваги рідин під впливом прикладених сил і дію рідин на занурені у них тверді тіла та стінки посудини.

2. Гідродинаміка – вивчає рух рідин та механічну взаємодію між рідиною і твердим тілом під час їхнього взаємного руху.

6.1. Закони гідростатики

З точки зору механіки рідини є середовищами, для яких у стані рівноваги дотичні напруження існувати не можуть. Тому в стані рівноваги сила тиску на площадку довільної орієнтації завжди перпендикулярна до її поверхні (тобто  ). З цього випливає закон Паскаля, який стверджує, що у стані спокою тиск у даній точці рідини передається однаково в усіх напрямах. На висновках з цього закону базується дія різних гідравлічних пристроїв.

Закон Паскаля строго справедливий, якщо на рідину не діють зовнішні сили. У полі зовнішніх сил на всі частинки рідини діють сили у напрямі дії сил поля. Зокрема, якщо трубу (рис. 19) довжиною і перерізом заповнити рідиною і встановити систему вертикально, т о на усі частинки рідини діятиме сила тяжіння, величина якої залежить від маси рідини: . На верхній шар рідини товщиною діє лише сила атмосферного тиску: . Шар тисне на нижні шари рідини з силою , де – густина рідини, що аналогічне виникненню додаткової сили тиску:

.

Нижні шари рідини зазнають додаткового тиску стовпа рідини:

(6.1)

Таким чином, гідростатичний тиск однорідного стовпа рідини висотою дорівнює: . У тих випадках, коли густина є функцією (передусім це стосується газів), в інтегралі у виразі (6.1) замість сталої густини буде присутня функція .

Іншим важливим законом гідростатики є закон Архімеда: на занурене в рідину (газ)тіло діє виштовхувальна сила, яка чисельно дорівнює вазі витісненої тілом рідини (газу).

Закон Архімеда має важливе значення для вирішення проблем повітроплавання (аеростати, дирижаблі й т. ін.) та проблем, пов’язаних із плаванням, стійкістю та рівновагою надводних та підводних суден.

6.2. Основні поняття гідродинаміки. Стаціонарний рух рідини. Рівняння Бернуллі

Рух рідини (газу) можна вивчати двома методами. Перший метод, запропонований Лагранжем, базується на розгляді рівнянь руху усіх частинок рідини і зводиться до визначення траєкторії, швидкості і прискорення частинки на будь-який момент часу. Використання методу Лагранжа пов’язане із значними математичними труднощами.

На практиці частіше використовують метод Ейлера. У даному розгляді говорять не про швидкість і прискорення окремих частинок рідини, а про швидкість і прискорення потоку рідини у кожній точці простору. Швидкість потоку рідини у даній точці простору залежить від координат точки і часу:

Розглянемо рух ідеальної рідини, абсолютно нестисливої і повністю позбавленої сил внутрішнього тертя. Для опису властивостей ідеальної рідини скористаємося підходом Ейлера. Введемо такі поняття.

1. П оле вектора швидкості для всіх точок простору, в яких присутня рідина.

2. Проведемо в рідині лінії таким чином, щоб дотичні до них у кожній точці співпадали з напрямом у цій точці (рис. 20). Ці лінії назвемо лініями течії. Густота розміщення ліній течії на рисунку пропорційна величині .

3. Трубка течії – частина рідини, що обмежена сукупністю ліній течії. Частинки рідини не можуть перетнути стінок трубки течії, бо завжди дотична до ліній течії.

4. Стаціонарне течіння рідини відповідає стану течіння рідини, при якому поле вектора швидкості не залежить від часу:

.

Важливою характеристикою течіння нестисливої рідини є теорема про нерозривність течії. Розглянемо трубку течії (рис.21) у стаціонарному потоці рідини настільки тонку, щоб швидкості рідини можна було вважати сталими у всіх точках будь-якого нормального поперечного перерізу. Обмежимо ділянку трубки течії двома нормальними перерізами  і  .

За час через перерізи перейдуть частинки, що були на відстанях не більших за для перерізу та за для перерізу . Для нестисливої рідини кількість частинок, що входять в об’єм, обмежений перерізами і за певний час , дорівнює кількості частинок, що виходять з об’єму за цей час. Тому: або звідки

, або (6.2)

Вираз (6.2) є математичним записом теореми про нерозривність струменя: маса рідини, що проходить за одиницю часу через кожний поперечний переріз трубки течії, для усіх перерізів однакова.

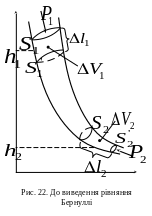Опис руху ідеальної рідини у полі сил тяжіння може бути здійснений за допомогою рівняння Бернуллі. Виберемо трубку течії, що перебуває у полі сил тяжіння з певним перепадом висот. Розглянемо переміщення порції рідини, що знаходиться між перерізами і (рис. 22).

За проміжок часу дана порція рідини зміститься у положення між перерізами і . За теоремою про нерозривність струменя об’єми рідини, що містяться між перерізами і та і , рівні між собою:

.

Зміну енергії всієї системи шукаємо як різницю енергій рідини, що перебуває в об’ємах та . Нехай густина рідини дорівнює . Вважаємо, що переміщення рідини малі, а тому на проміжках і швидкості і , а також зовнішні тиски і можна вважати сталими.

Зміна енергії порції рідини чисельно дорівнює роботі сил тиску та . Ця робота дорівнює:

.

Зміна енергії порції рідини складається зі зміни кінетичної та зміни потенціальної енергії:

.

Прирівняємо та і отримаємо:

,

або в загальному вигляді для довільної висоти :

(6.3)

Вираз (6.3) називають рівнянням Бернуллі. У цьому виразі – динамічний тиск, що чисельно дорівнює кінетичній енергії одиниці об’єму рідини, – гідравлічний тиск (тиск стовпа однорідної рідини висотою під дією сили тяжіння), – статичний тиск, зумовлений дією зовнішніх сил.

Для горизонтальної течії рідини рівняння Бернуллі набуває вигляду:

(6.4)

З виразу (6.4) випливає, що в місцях, де швидкість течії більша, тиск менший. Залежність тиску рідини від її швидкості лежить в основі дії багатьох пристроїв. Це явище використовується, зокрема, у пульверизаторах, карбюраторах та водоструменевих насосах. На рис. 23 показано схему найпростішого водоструменевого насоса. Воду з водогону подають через трубку, що має звуження (сопло), з якого вода витікає з великою швидкістю. Це призводить до зниження статичного тиску в даному місці і внаслідок з відкачуваної посудини засмоктується повітря. Насос дозволяє отримувати тиски газів майже у 100 разів менші за атмосферний (принципово мінімальний тиск не може бути нижчим за тиск насиченої пари води за даної температури).

Для експериментального вимірювання тиску в рідині та швидкості потоку рідини використовують прості пристрої у вигляді зігнутих манометричних трубок, поміщених у потік рідини. Найпростішими із них є зонд та трубка Піто (рис. 24).

Трубка Піто (рис.24а) є зігнутою манометричною трубкою з відкритим кінцем, що повернутий назустріч течії рідини. За допомогою трубки Піто вимірюють повний тиск рідини у горизонтальній трубі: . Статичний тиск вимірюють з допомогою зонда (рис. 24б). Зонд являє собою зігнуту трубку, запаяну в частині, повернутій у напрямі потоку, і з малим отвором у бічній стінці.

Для вимірювання динамічного тиску (а таким чином – швидкості рідини) використовують манометричну трубку Прандтля (рис. 24в), що є комбінацією трубки Піто і зонда. З різниці рівнів стовпів рідини у цих трубках знаходимо і кінцево роз-раховуємо швидкість рідини:

(6.5)

Цікавою для практики є задача про витікання рідини через малий отвір у бічній стінці широкої посудини (рис. 25).

Нехай висота стовпа рідини до центра отвору . На вільну поверхню рідини і на струмінь, що витікає діє зовнішній статичний тиск , що дорівнює атмосферному. Запишемо рівняння Бернуллі:

.

Оскільки поперечний переріз трубки набагато більший за площу отвору , , а тому вважаємо . Тому

(6.6)

В ираз (6.6) називають формулою Торрічеллі. Об’єм рідини, що витікає через отвір за одиницю часу: . За час через отвір витікає рідина масою . Ця рідина має швидкість , а тому її імпульс . Згідно з третім законом Ньютона посуд з рідиною отримує від рідини, що витікає імпульс - , а тому на посудину діє сила реакції рідини:

(6.7)

або

. (6.7а)

Розглянемо реакцію потоку рідини на стінки зігнутої труби. Нехай у зігнутій під деяким кутом трубі постійного перерізу встановився стаціонарний потік рідини (див. рис. 26). За теоремою про нерозривність струменя швидкість протікання рідини буде однакова за величиною в кожному перерізі.

Розглянемо об’єм труби обмежений перерізами і . Через переріз за одиницю часу в об’єм вливається кількість рідини яка вносить в об’єм імпульс . За одиницю часу з об’єму витікає кількість рідини , що виносить з об’єму імпульс . Таким чином, стінки трубки надають рідині за одиницю часу приріст імпульсу .

Згідно з другим законом Ньютона приріст імпульсу тіла за одиницю часу чисельно рівний силі, що діє на тіло. Таким чином зігнута трубка діє на струмінь рідини з силою .

Згідно з третім законом Ньютона рідина діє на стінки трубки з силою, яка за величиною дорівнює , але протилежна їй за напрямом. Тому сила реакції струменя на стінки труби рівна:

. (6.8)