Задача а.Р. Ржаницына об устойчивости сжатого стержня в условиях ограниченной ползучести

Все материалы обладают тремя основными свойствами – упругости, пластичности и вязкости. При длительной эксплуатации конструкции, которая содержит сжатый силами Р стержень, может проявиться свойство вязкости материала в виде его ползучести либо релаксации напряжений.. Эти явления при ограниченной ползучести (для таких материалов, как бетон, полимеры,композиты) описываются законом Кельвина:

, (9.135)

где время релаксации, – модуль продольной упругости, – длительный модуль упругости, и - скорости напряжений и деформаций.

Рассмотрим шарнирно опёртый стержень, сжатый силами (рис. 9.45).

Рис. 9.45

Из условий равновесия отсечённой части стержня имеем , , . Деформация и её скорость при изгибе стержня:

(9.136)

Умножая (9.135) на , интегрируя по площади стержня и используя (9.136), получаем:

(9.137)

где

Подставляя в (9.132) выражения находим:

(9.138)

Примем для прогиба и его скорости выражения

.

Тогда из (9.138) получаем:

(9.139)

где - (9.140)

бифуркационнные нагрузки Л. Эйлера и А.Р. Ржаницына.

Обозначим: . (9.141)

Тогда уравнение (9.139) преобразуется к виду

(9.142)

Разделяя переменные и интегрируя, получаем:

или, после потенцирования,

.

Постоянную находим из начального условия при

В результате получаем:

(9.143)

Если прогиб по методу проб Эйлера на устойчивость, то выражение (9.142) даёт закон поведения прогиба после снятия возмущающей поперечной силы. Возможны три состояния процесса изгиба стержня во времени . При коэффициент , и из (9.143) следует, что при прогиб , т.е. стержень устойчив, т.к. возвращается со временем к своей начальной прямолинейной форме (рис. 9.45).

Рис. 9.46

При имеем , и при прогиб , т.е. стержень неустойчив. При имеем и решение уравнения (9.137) Стержень остаётся в безразличном состоянии на границе между устойчивым и неустойчивым состояниями процесса выпучивания.

Таким образом, мы обнаруживаем что при сжатый стержень обладает свойством длительной устойчивости, т.к. после снятия возмущения остаётся пребывать в малой окрестности исходного невозмущенного состояния при

Реальные стержни обладают начальными несовершенствами своей прямолинейной геометрической формы. Пусть – начальный технологический прогиб оси стержня. Будем смотреть на него как на малый возмущающий фактор. Тогда кривизна изогнутой оси стержня в процессе его деформирования:

а относительные деформации и напряжения:

Умножим вновь (9.122) на и, интегрируя, получим уравнение

(9.144)

Полагая в (9.144):

и учитывая обозначение (9.141), приходим к уравнению

(9.145)

Решение уравнения (9.140) имеет вид

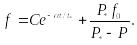(9.146)

Начальным условием при для решения (9.146) является статическое решение (9.106) задачи о выпучивании упругого стержня с начальным прогибом:

.

Удовлетворяя решение (9.141) этому условию, получим:

и общее решение:

(9.147)

При имеем и поэтому из (9.147) при получаем, что прогиб ограничен и стремится к значению (рис. 9.46):

.

При имеем и поэтому из (9.141) при получаем .

Рис. 9.46

Процесс выпучивания во времени неограничен и, следовательно, неустойчив (рис. 9.47).

При коэффициент , и из уравнения (9.140) получаем:

При нагрузке впервые процесс выпучивания стержня из материала с ограниченной ползучестью становится неустойчивым. Поэтому названа длительной критической нагрузкой А.Р. Ржаницына.

Устойчивость упругого стержня в условиях неограниченной ползучести

Ползучесть некоторых полимерных материалов в установившейся стадии является нелинейной и описывается при вязкоупругих деформациях законом:

(9.148)

Тогда постановка задачи об устойчивости на бесконечном интервале времени не имеет смысла. При ограниченной ползучести задача об устойчивости сжатого стержня имеет смысл, в соответствии с концепцией устойчивости, если сжимающая нагрузка больше нагрузки надёжности устойчивых состояний. В противном случае стержень может разрушиться от чрезмерного продольного изгиба вследствие развивающихся деформаций ползучести. Инженерной задачей является определение критического времени, в течение которого стержень способен воспринимать внешнюю нагрузку.

Рассмотрим стержень идеализированного двутаврового поперечного сечения (рис. 9.48), шарнирно опёртый по краям и сжатый силами .

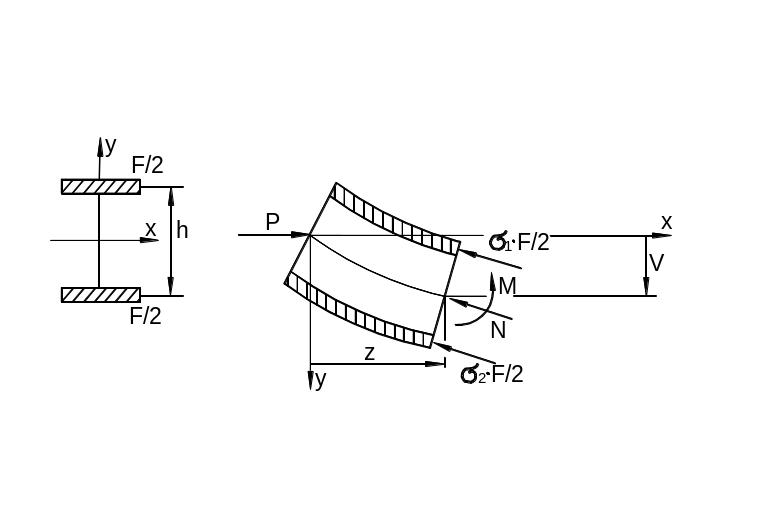
Рис. 9.47

Пусть - длина стержня, площадь каждой полки составляет , и их размеры малы по сравнению с высотой сечения , так что можно считать напряжения в каждой полке распределены равномерно. Площадью тонкой стенки пренебрегаем. Определяем момент инерции поперечного сечения:

Уравнение равновесия части стержня, отсечённого на расстоянии от края (рис. 9.47), записываем в виде:

(9.149)

где и - напряжения в полках соответственно на вогнутой и выпуклой сторонах; – сжимающая сила; – прогиб в сечении.

Деформация в стержне:

.

В частности, для полок двутавра получаем:

(9.150)

Вычитая деформации друг из друга, находим дифференциальное уравнение изогнутой оси стержня:

(9.151)

Введём безразмерные прогиб и осевую координату:

Тогда уравнения равновесия (9.149), (9.151) примут вид

(9.152)

(9.153)

где среднее напряжение в поперечном сечении стержня.

Из уравнений (9.152) найдём:

(9.154)

Дифференцируя (9.152), (9.153) по , получим:

(9.155)

(9.156)

Подставив (9.154), (9.155) в (9.148), найдём для каждой из полок:

(9.157)

Подставив (9.157) в (9.156) и приняв , найдём:

(9.158)

Примем для определения прогиба выражение:

(9.159)

Разложив нелинейный член в (9.158) в ряд Фурье по синусам и приравняв нулю коэффициент при получим:

(9.160)

Здесь

Разделив переменные и проинтегрировав (9.160) от до получим:

(9.161)

Здесь безразмерный мгновенный прогиб, определяемый из решения упругой задачи:

Выражение (9.161) характеризует время, необходимое для достижения заданного прогиба при данном мгновенном прогибе . Критическая ситуация, характеризуемая исчерпанием несущей способности стержня и быстрым нарастанием прогибов, наступает при некотором критическом времени , когда В этом случае из (9.156) следует:

Если , то , т.е. наступает мгновенная потеря устойчивости. При критическое время увеличивается. На рис. 9.48 а,б приведены зависимости безразмерного прогиба от времени для и критического времени от безразмерного параметра нагрузки . В расчётах было принято

При прогибы стержня неограниченно увеличиваются.

При линейной неограниченной ползучести ( ) вместо уравнения (9.158) получаем:

Приняв прогиб в той же форме (9.159), имеем:

а после интегрирования:

Следовательно, при т.е. бесконечно большой прогиб реализуется в течение бесконечно большого времени, иными словами, в условиях неограниченной ползучести конечного, отличного от нуля предела длительной устойчивости не существует.

а) б)

Рис. 9.48

Устойчивость плоской формы изгиба балок

Балка, изогнутая в своей плоскости, может потерять устойчивость своей плоской формы изгиба при некотором критическом значении внешней нагрузки и выпучиться в сторону (рис. 9.51). При этом поперечное сечение балки повернётся, т.е. балка будет испытывать изгиб с кручением.

Рассмотрим свободно опёртую балку длиной , изгибаемую по концам моментом (рис. 9.51,а). В докритическом состоянии дифференциальное уравнение изогнутой оси имеет вид:

(9.162)

Интегрируя дважды, получим:

Рис. 9.49

Так как при , прогиб , то и потому

Максимальное значение прогиба:

На рис. 9.50 показан график зависимости от значений момента .

Кружочек отвечает моменту появления пластических деформаций (пределу пропорциональности ), сплошной кружочек – предельному моменту , при котором происходит образование пластического шарнира и исчерпание несущей способности балки, тонкая линия соответствует упругопластическому поведению балки.

Если сечение балки узкое (высокое), как у полосы или двутавра (рис. 9.47), то при некотором критическом значении изгибающего момента произойдет бифуркация решения, и балка получит боковое выпучивание с закручиванием.

Рис. 9.50

Пусть угол характеризует наклон изогнутой оси балки в плоскости при боковом отклонении, а - угол закручивания в некотором произвольном сечении . Представим момент в сечении в виде вектора по правилу правого винта (буравчика). Тогда, проецируя на оси , , , отнесённые к сечению (рис. 9.51,г), получим:

Следовательно, дифференциальные уравнения изгиба и кручения принимают вид

где учтена малость величин , , , .

Для прямоугольника:

Первое уравнение совпадает с (9.162) и описывает докритический изгиб после точки бифуркации .

Дифференцируя третье уравнение по и исключая с помощью второго уравнения производную получаем:

(9.163)

где

(9.164)

Общее решение уравнения (9.163) имеет вид

(9.165)

Удовлетворяя (9.165) граничным условиям:

при

получим (9.166)

Если положим в (9.166) , то получим тривиальное решение, при котором балка не получает бокового выпучивания. Если то откуда и, согласно (9.159), находим:

Более трудным оказывается решение задач о плоской форме изгиба при поперечном изгибе. Так, для консольной балки, нагруженной поперечной силой, имеем:

При изгибе шарнирно опёртой балки длиной силой Р, приложенной посередине пролёта, имеем:

а при действии распределённой нагрузки :

Энергетический метод определения критических нагрузок

Энергетический метод представляет собой один из способов определения критических нагрузок. Пусть согласно методу проб Эйлера сжатый силами стержень не вернулся в исходное состояние равновесия (рис. 9.51).

а) б)

Рис. 9.51

При этом подвижная шарнирная опора переместится на величину так, что сила совершит работу а стержень выпучится (изогнётся). Энергия изгиба:

Учитывая, что получим:

(9.167)

Рассмотрим элемент стержня . Этот элемент к моменту потери устойчивости уже сжат, и при упругом изгибе его длина не меняется. После изгиба элемент займёт положение . Поэтому укорочение стержня по направлению z будет:

Сближение концов стержня при потере устойчивости:

(9.168)

Работа, совершаемая силой , определится соотношением:

Приравнивая выражение (9.167), (9.168), получим:

(9.169)

Если точная функция прогибов стержня известна, то значение критической силы находится просто. Для шарнирно опёртого стержня что даёт известную формулу:

В общем случае функция прогибов неизвестна, и её задают приближённо. Пусть, например, в той же задаче

Тогда

Как видно, при приближённом задании прогиба, удовлетворяющем граничным условиям, критическое значение силы больше, чем при точном задании прогиба.

Можно показать в общем случае, что по сравнению со всеми функциями прогиба , удовлетворяющим граничным условиям, истинная функция прогиба даёт минимальное значение .

Пример 3.

Найти критическую силу для сжатой колонны (рис. 9.52).

Рис. 9.52

Граничные условия для данной задачи имеют вид:

при .

Примем для прогиба выражение:

(9.170)

удовлетворяющее граничным условиям. Сохраним в (9.170) два члена ряда:

(9.171)

После подстановки выражения прогиба (9.171) в (9.164) и интегрирования, получим:

(9.172)

Если выражение прогиба положим , т.е. сохраним только один член, то найдём минимальное значение силы Р, равное:

что даёт погрешность по отношению к точному значению равную 21,6%.

При двух значениях постоянных , минимальное значение найдём, дифференцируя (3) по и приравнивая выражение к нулю:

или

откуда

или

Наименьшее значение критической силы даёт первый корень:

,

что отличается от точного решения только на 0,92 %.