Практический инженерный метод расчёта на устойчивость ф. Ясинского

Теоретическое решение, полученное Эйлером, оказалось применимым на практике лишь для очень ограниченной категории стержней, а именно, тонких и длинных, с большой гибкостью. Между тем, в конструкциях очень часто встречаются стержни с малой гибкостью. Попытки использовать формулу Эйлера для вычисления критических напряжений и проверки устойчивости при малых гибкостях вели иногда к весьма серьезным катастрофам, да и опыты над сжатием стержней показывают, что при критических напряжениях, больших предела пропорциональности, действительные критические силы значительно ниже определенных по формуле Эйлера.

Таким образом, надо найти способ вычисления критических напряжений и для тех случаев, когда они превышают предел пропорциональности материалов, например, для стержней из мягкой стали при гибкостях от 0 до 100.

Необходимо сразу же отметить, что в настоящее время важнейшим источником для установления критических напряжений за пределом пропорциональности, т.е. при малых и средних гибкостях, являются результаты экспериментов. Имеются попытки и теоретического решения этой задачи, но они скорее указывают путь к дальнейшим исследованиям, чем дают основания для практических расчетов.

Прежде всего надо выделить стержни с малой гибкостью, от 0 примерно до 30—40; у них длина сравнительно невелика по отношению к размерам поперечного сечения. Например, для стержня круглого сечения гибкости 20 соответствует отношение длины к диаметру, равное 5. Для таких стержней трудно говорить о явлении потери устойчивости прямолинейной формы всего стержня в целом в том смысле, как это имеет место для тонких и длинных стержней.

Эти короткие стержни будут выходить из строя главным образом за счет того, что напряжения сжатия в них будут достигать предела текучести (при пластичном материале) или предела прочности (при хрупких материалах). Поэтому для коротких стержней, до гибкости примерно 30-40, критические напряжения «будут равны, или немного ниже (за счет наблюдающегося все же некоторого искривления оси стержня), соответственно или (сталь), или (чугун, дерево).

Таким образом, мы имеем два предельных случая работы сжатых стержней: короткие стержни, которые теряют грузоподъемность в основном за счет разрушения материала от сжатия, и длинные, для которых потеря грузоподъемности вызывается нарушением устойчивости прямолинейной формы стержня. Количественное изменение соотношения длины и поперечных размеров стержня меняет и весь характер явления разрушения. Общим остается лишь внезапность наступления критического состояния в смысле внезапного резкого возрастания деформаций.

В сжатых стержнях большой гибкости, для которых применима формула Эйлера, после достижения силой Р критического значения обычно наблюдается резкий рост деформаций. До этого момента прогибы, как правило, растут с ростом нагрузки, но остаются незначительными. Теоретически можно было бы ожидать, что до критической силы стержень будет оставаться прямым; однако ряд неизбежных на практике обстоятельств — начальная кривизна стержня, некоторый эксцентриситет приложения нагрузки, местные перенапряжения, неоднородность материала — вызывают небольшие прогибы и при сжимающих силах, меньших критических.

Подобный же характер имеет и зависимость укорочений от напряжения при сжатии коротких стержней; мы имеет ту же внезапность роста деформаций при определенной величине напряжений (когда ).

Нам остается теперь рассмотреть поведение сжатых стержней при средних величинах гибкости, например для стальных стержней при гибкостях от 40 до 100; с подобными значениями гибкостей инженер чаще всего встречается на практике.

По характеру разрушения эти стержни приближаются к категории тонких и длинных стержней; они теряют свою прямолинейную форму и разрушаются при явлениях значительного бокового выпучивания. При опытах для них можно отметить наличие ясно выраженной критической силы в «эйлеровом» смысле; критические напряжения получаются выше предела пропорциональности и ниже предела текучести для пластичных и предела прочности для хрупких материалов.

Однако потеря прямолинейной формы и понижение критических напряжений по сравнению с короткими стержнями для этих стержней «средней» гибкости связаны с такими же явлениями нарушения прочности материала, какие вызывают потерю грузоподъемности в коротких стержнях. Здесь комбинируются и влияние длины, понижающее величину критических напряжений, и влияние значительного роста деформаций материала при напряжениях за пределом пропорциональности.

Экспериментальное определение критических сил для сжатых стержней производилось неоднократно как у нас, так и заграницей. Особенно обширный опытный материал собрал проф. Ф. Ясинский, составивший таблицу критических («ломающих») напряжений в. зависимости от гибкости для целого ряда материалов и положивший начало современным методам расчета сжатых стержней на устойчивость.

Рассмотрим две простейшие стержневые системы (рис. 9.21).

Узел А в обоих примерах испытывает одинаковое по модулю воздействие реактивных сил. Однако условия работы среднего стержня 2 будут различны. В схеме на рис. 9.21,а все стержни работают на растяжение, и мы должны потребовать выполнения условия прочности для растягивающих напряжений:

.

а) б)

Рис. 9.21

Во втором случае на рис. 9.21,б средний стержень 2 работает на сжатие, а два других - на растяжение, и мы кроме условия прочности на растяжение должны обеспечить условие прочности на сжатие:

Однако этого недостаточно, т.к. сжатый стержень может потерять устойчивость. Поэтому мы должны потребовать выполнения условия устойчивости:

Ф. Ясинский ввёл понятие коэффициента продольного изгиба (снижения основного допускаемого напряжения):

(9.56)

и записал условие устойчивости в виде

(9.57)

или

где - называют расчётным напряжением.

Поначалу Ф. Ясинский считал . Тогда:

Для имеет место формула Эйлера и условие для предельной гибкости:

откуда следует

Тогда для коэффициента продольного изгиба получаем:

.

Следовательно, коэффициент изменяется в зависимости от по закону гиперболы.

Для воспользуемся формулой касательного модуля либо её аппроксимацией в форме Джонсона:

,

для коэффициента получаем формулу

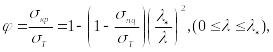
из которой видно, что изменяется по закону параболы.

На рис. 9.22 представлен график от для стали 3 В этом случае В последствии в СНиПе было уточнено отношение коэффициентов запаса , и расчёт стал производиться по формуле (9.56):

.

Рис. 9.22

Для стали обычно Коэффициент запаса на устойчивость для принимается постоянным: При Точка В, в которой снижается до значения

что отмечено на рис. 9.22 в точке В.

Для стержней из дерева в СНиПе рекомендуется формула

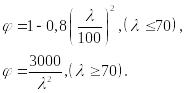
Для сосны

Для коэффициента продольного изгиба составлены таблицы. Ниже приведена такая таблица для ряда материалов (табл. 9.2).

Различают три типа расчёта на устойчивость: проверочный, определение допускаемой силы и проектный расчёт. При проверочном расчёте известны действующая сила Р, размеры стержня , допускаемое напряжение на сжатие способ закрепления стержня, т.е. коэффициент . Вычисляется гибкость стержня и по таблице коэффициентов для данного материала находится сам коэффициент При этом допускается линейная интерполяция , если она не кратна десяти. Затем производится проверка выполнения расчётной формулы (9.57) на устойчивость:

При проектном расчёте заданы сила Р, длина стержня , коэффициент приведения длины , Неизвестными остаются площадь сечения и коэффициент продольного изгиба . Поэтому расчёт может быть выполнен только методом последовательных приближений в таком порядке: задаются каким либо значением коэффициента , например ; рассчитывают по нему требуемую площадь Затем рассчитывается момент инерции , радиус инерции , уточняется площадь , вычисляется гибкость и по таблице находится соответствующий коэффициент После этого рассчитывается расчётное напряжение:

Если разница между расчётным и допускаемым напряжением более 5%, то рассматривается второе приближение с новым значением коэффициента:

и расчёт повторяется в указанном выше порядке до тех пор пока разница между и станет не более .

Таблица 9.2. Коэффициенты продольного изгиба

	Сталь 3,4	Сталь 5	Сталь 15ХСНД	Сплав Д16Т	Чугун	Железо- бетон	Дерево (сосна)
0	1	1	1	1	1	1	1
10	0,99	0,98	0,98	1	0,96	1	0,99
20	0,97	0,95	0,95	1	0,91	1	0,99
30	0,95	0,92	0,93	0,84	0,81	1	0,93
40	0,92	0,89	0,90	0,70	0,69	1	0,87
50	0,89	0,86	0,83	0,57	0,57	1	0,80
60	0,86	0,82	0,78	0,46	0,44	0,83	0,71
70	0,81	0,76	0,71	0,35	0,34	0,73	0,61
80	0,75	0,70	0,63	0,27	0,26	0,64	0,49
90	0,69	0,62	0,54	0,21	0,20	0,57	0,38
100	0,60	0,51	0,45	0,17	0,16	0,52	0,31
110	0,52	0,43	0,39	0,14	-	-	0,25
120	0,45	0,38	0,33	0,12	-	-	0,22
130	0,40	0,32	0,29	0,10	-	-	0,18
140	0,36	0,28	0,26	0,087	-	-	0,16
150	0,32	0,26	0,23	0,076	-	-	0,14
160	0,29	0,24	0,21	-	-	-	0,12
170	0,26	0,21	0,19	-	-	-	0,11
180	0,23	0,19	0,17	-	-	-	0,10
190	0,21	0,17	0,15	-	-	-	0,09
200	0,19	0,16	0,13	-	-	-	0,08

При сжатии стержень изгибается в направлении наименьшей жесткости, его гибкость тем больше, чем меньше радиус инерции сечения. Отсюда вытекают следующие требования, которым должно удовлетворять сечение стержня, работающего на продольный изгиб:

1) стержень должен обладать одинаковой жесткостью по всем направлениям. Для этого моменты инерции, а следовательно, и радиусы инерции сечения относительно главных осей должны быть равны. Если же условия закрепления концов стержня в обеих главных плоскостях неодинаковы, как, например, шатун двигателя, то для получения одинаковой жесткости моменты инерции сечения относительно главных осей должны быть подобраны соответственно различными;

2) момент, а следовательно, и радиус инерции сечения при данной величине его площади должен быть возможно большим. Для этого элементы сечения должны быть удалены, возможно, дальше от его центра тяжести.

Указанным требованиям полностью удовлетворяют пустотелые стержни круглого и квадратного сечений. Стенки пустотелых стержней нельзя делать слишком тонкими, т. к. они могут потерять устойчивость, покрывшись волнистыми складками.

Для повышения устойчивости стенок принимают продольные ребра жесткости или поперечные распорки (диафрагмы), помещаемые на определенных расстояниях.

По степени рациональности известные сечения можно распределить следующим образом: трубчатое сечение, коробчатое, двутавровое, состоящее из швеллеров, квадратное, круглое, прямоугольное.

Пример 1.

Стальной стержень длиной двутаврового сечения №18, шарнирно закреплённый на одном и жёстко на другом краях, сжимается силами . Требуется определить допускаемое и критическое значения силы , если

Решение.

Из сортамента стального проката для двутавра №18 находим F = 23,4 см², Коэффициент приведения длины Ясинского для данного типа закрепления гибкость стержня

Так как то критическая сила может быть определена по формуле Эйлера:

По таблице коэффициентов после интерполяции находим Вычисляем допускаемое значение внешней силы:

Коэффициент запаса на устойчивость

Если принять длину , то В этом случае для определения критической силы использовать формулу Эйлера нельзя. Воспользуемся формулой Джонсона:

Допустимая нагрузка:

Коэффициент запаса

Если воспользоваться формулой Ясинского, то

Коэффициент запаса:

Пример 2.

Подобрать размеры круглого поперечного сечения стержня длиной из дерева (сосна), нагруженного силой Р = 100 кН, если Один конец стержня жёстко защемлён, а другой свободен от закрепления

Решение.

Условия устойчивости записываем в виде

Подбор диаметра D сечения производим методом последовательных приближений.

Первое приближение. Принимаем Тогда:

Так как то

Подбор диаметра ведём с точностью до целого см. Для найденного диаметра D = 13см находим:

Находим гибкость По таблице коэффициентов с учётом интерполирования находим

Вычисляем:

Сравнивая с , видим, что в стержне будет перенапряжение в или на 429%. Поэтому следует рассмотреть второе приближение.

Второе приближение. Задаёмся новым значением:

Находим

Диаметр Далее после округления размера диаметра до целых значений см вычисляем:

По таблице находим и рассчитываем:

Перенапряжение составляет т.е. 83%. Поэтому необходимо рассмотреть третье приближение.

Третье приближение. Принимаем

Вычисляем:

Находим диаметр

Округляем диаметр до целых значений см и получаем D₃ = 20см. Корректируем новую площадь:

Вычисляем:

По таблице 9.2 для находим с учётом интерполяции Расчётное сопротивление:

Недонапряжение т.е. 7,7%.

На этом расчёт можно прекратить и принять размер диаметра D = 20см.