Основы теории пластичности

Рассмотрим основ­ные особенности характера деформирования материалов при их нагружении в упруго-пластической стадии. При напряжениях, превышающих предел упругости, после разрузки наблюдаются заметные остаточные деформации. Свойство материалов относительно неспособности восстанавливать первоначальные размеры образцов после их разгрузки за счет возникновения остаточных деформаций, называется пластич­ностью.

Физические соотношения, взятые в основу теории, позволя­ющие определить переход напряженно-деформированного сос­тояния от упругой стадии к упруго-пластической и описать про­цесс деформирования тела с учетом пластических свойств мате­риалов, называются теорией пластичности.

Учет пластических свойств материалов является чрезвычайно важным этапом в плане совершенствования методов расчета конст­рукций. Если конструкции из хрупких материалов вплоть до стадии разрушения при действии внешних сил не развивают заметных пластических деформаций, то для конструкций из пластических материалов основные деформации формируются именно за счет возникновения пластических деформаций. Так например, полные деформации, соответствующие концу площадки текучести на ре­альной диаграмме, для многих материалов в 30 - 40 раз превышают деформации, соответствующие концу линейного участка.

В настоящее время существуют две теории пластичности. Их различие заключается в конкретной записи физических соотноше­ний.

В деформационной теории пластичности, разработан­ной А.А.Ильюшиным, взамен закона Гука устанавливаются новые соотношения между напряжениями и деформациями.

Во второй теории - теории течения, физические соотноше­ния связывают напряжения с приращениями деформаций или ско­ростями деформаций.

Как показывают экспериментальные исследования, деформаци­онная теория пластичности справедлива при относительно неболь­ших пластических деформациях для простого нагружения, т.е. ког­да все внешние нагрузки изменяются пропорционально во време­ни.

Теория течения является эффективным при изучении процес­сов, связанных с возникновением больших деформаций и при сложном нагружении, т.е. когда нагрузки, прикладываемые к телу, изменяются во времени независимо друг от друга.

Здесь ограничимся рассмотрением только деформационной теории пластичности.

Процесс деформирования материалов можно условно разделить на две стадии. Начальная стадия - упругое деформирование. Компоненты тензоров напряжений и деформаций при этом связа­ны законом Гука. Для реальных инженерных задач, связанных с определением напряженно-деформированного состоя­ния тела, как в упругой, так и в упруго-пластической ста­дии деформирования, предварительно необходимо установить: во-первых, условие перехода от упругой стадии деформирования к пластической стадии и, во-вторых, установить физические зависи­мости во второй стадии деформирования.

Условия перехода от упругого состояния к пластическому могут быть определены по формулам одной из гипотез метода предельного равновесия.

Как это было изложено в пункте «Основные положения метода предельного равновесия», наиболее приемлемыми являются гипотезы максимальных касательных напряже­ний и энергии формоизменения. При этом, для построения соотношений пластичности гипотеза энергии формоизменения яв­ляется наиболее приемлемой, согласно которой переход из упруго­го состояния в пластическое происходит тогда, когда величина

(20.4)

называемая интенсивностью напряжений, достигает определенной величины, равной пределу текучести материала при одноосном напряженном состоянии, т.е.

. (20.5)

С учетом физических соотношений (10.18) и (10.19) выражение (20.4) принимает вид:

, (20.6)

где принято обозначение:

(20.7)

называемое интенсивностью деформаций.

Следовательно, соотношение (20.6), следует рассматривать как одну из форм выражения обобщенного закона Гука.

Выражения интенсивности напряжений и интенсивности де­формаций, записанные через главные напряжения и деформации можно представить в виде:

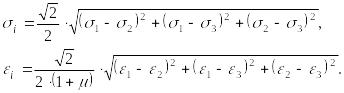(20.8)

В основу деформационной теории пластичности заложены сле­дующие гипотезы.

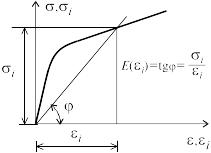
Рис. 20.1

Первая гипотеза устанавливает связь между интенсивностью напряжений и интенсивностью деформаций (рис. 20.1), и гла­сит, что она не зависит от вида напряженного состояния, т.е.

, (20.9)

где - является переменной величиной и зависит от значе­ния . Соотношение (20.9) яв­ляется единым для всех видов напряженного состояния.

Согласно второй гипотезе - изменение объема является чисто упругой. Это положение хорошо согласуется с экспериментальными данными, так как при всестороннем сжатии в материалах заметных плас­тических деформаций не обнаруживается.

При деформировании материалов пластические деформации, как правило, существенно больше упругих и, учитывая, что объ­емная деформация является величиной порядка упругих удлине­ний, поэтому принимается, что при пластическом деформировании изменение объема пренебрежительно мало. На основании этого по­ложения вводится гипотеза, что в пластической стадии деформи­рования материал считается несжимаемым.

Откуда следует, что в пластической стадии деформирования можно коэффициент Пуас­сона принимать равным = 0,5.

Сначала определим физические соотношения при одноосном растяжении, когда

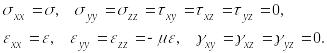
Из (20.4) и (20.7), соответственно получим и , что подтверждает первое положение теории, что аналитическое вы­ражение (20.9) едино для всех видов напряженного состояния. Данное обстоятельство позволяет определить переменный модуль деформирования по диаграмме ~ , т.е. .

В заключение, аналогично соотношениям (10.18)-(10.19) запи­шем физические соотношения между напряжениями и деформа­циями при пластической стадии деформирования тела:

(20.10)

где является модулем деформации при сдвиге, кото­рый определяется следующим образом:

. (20.11)

Приведенные физические соотношения деформационной тео­рии пластичности являются справедливыми при простых нагруже­ниях, т.е. только в тех случаях, когда все внешние силы на всех этапах нагружения во времени изменяются пропорционально. В данном случае заметим, что главные оси напряженного состояния при изменении внешних сил сохраняют свое направление незави­симо от стадии деформирования.

Для наглядности ниже рассмотрим наиболее представительные примеры расчета конструкций по методу предельного равновесия.

Определение предельного состояния системы при растяжении-сжатии

Для статически определимой системы, в элементах которой возникают лишь продольные усилия, расчеты на прочность по допускаемым напряжениям и по предельным нагрузкам дают один и тот же результат. Результаты аналогичных расчетов статически неопределимой системы различны.

Пример 1.

Рассмотрим систему, представляющую со­бой абсолютно жесткую балку, с одним концом шарнирно опертую, и подвешенную на трех одинаковых идеально упруго-пластических подвесках, длиной l, площадью поперечного сечения А, модулем упругости материала Е, при заданной схеме нагружения силой Р (рис.20.2, а). Заданная система дважды статически неопределима.

Решение.

По мере роста силы P, подвески 1, 2, 3 поэтапно будут пере­ходить в пластическое состояние, причем напряжения в каждой подвеске не могут превышать .

Выделим следующие стадии деформирования заданной систе­мы.

Первая стадия: все подвески работают упруго. Для опре­деления реакций в подвесках составляем уравнение равновесия:

. (20.12)

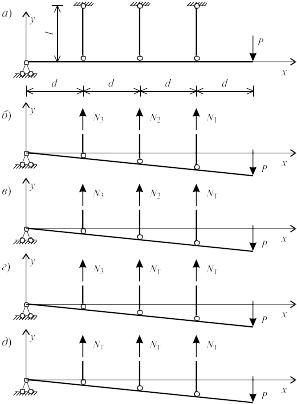
Рис. 20.2

Для определения величин усилий в подвесках N₁, N₂ и N₃ не­обходимо составить еще два уравнения совместности. Учитывая, что балка абсолютно жесткая и деформации в подвесках пропор­циональны возникающим в них усилиям, то из условия подобия треугольников (рис.20.1, б), имеем:

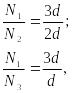
откуда

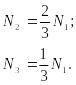(20.13)

Тогда из (20.12) с учетом (20.13) опре­деляются реакции во всех подвесках:

(20.14)

Вторая ста­дия: при некото­ром значении P, сначала наи­более нагруженная первая подвеска, переходит в пластическое состояние, то есть (рис.20.2, в). При этом из (20.13) можно установить, что в остальных подвесках усилия будут равны:

; . (20.15)

Подставляя значения усилий в уравнение равновесия (20.12), по­лучим:

,

откуда и определим величину внешней силы Р, при котором систе­ма переходит во второе состояние:

. (20.16)

Третья стадия: при дальнейшем росте значения силы P, и вторая подвеска переходит в пластическое состояние, то есть N₁ = N₂ = (рис.20.2, г). При этом, из второго и третьего со­отношения (20.14), значение усилия в третьей подвеске будет равно:

. (20.17)

Из уравнения равновесия (20.12), с учетом значения усилий в подвесках в третьем состоянии, получим:

. (20.18)

Четвертая стадия - предельное состояние: в этом состоянии усилия во всех трех подвесках равны своему предель­ному значению, т.е. (рис.20.2, д). Уравнение равновесия (20.12), при этом принимает вид:

, (20.19)

откуда и определяется предельная величина внешней силы:

. (20.20)

Далее определим перемещение f_i балки в точке приложения внешней силы P в различных стадиях работы заданной системы.

При переходе заданной системы от первого стадии деформиро­вания ко второму, имеем:

; .

При переходе заданной системы от второй стадии к третьей, имеем:

; .

И наконец, при переходе системы от третьей стадии к пре­дельному состоянию, получим:

.

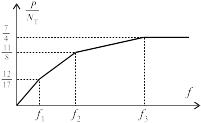
Рис. 20.3

Зависимость f от P показана на рис.20.3. Она изображается ло­маной линией, которая после предельного равновесного состояния становится горизонтальной, то есть после того, как напряжения достигнут предела текучести во всех трех подвесках. Откуда следует, что при постоянной , пе­ремещение f беспредельно возрас­тает, т.е. происходит разрушение системы.

Как видно из приведенного примера, расчет даже для такой простой системы оказывается до­вольно громоздким, хотя он дает возможность находить не только предельную силу, но и описать поведение конструкции в процес­се ее нагружения. На практике, при расчете систем с учетом плас­тических деформаций рассматривают только предельное состояние.