
- •Часть 3
- •Содержание
- •1. Планирование маркетинговой политики. Методы оптимизации маркетинговых затрат (реклама, товародвижение и сбыт)
- •1.1. Основные элементы маркетинга.
- •1.2. Игровая модель управления конкурентоспособностью продукции.
- •1.2.1. Прямая задача.
- •1.2.2. Обратная задача.
- •1.3. Марковская модель управления затратами на рекламу.
- •1.3.1. Типовой пример.
- •1.3.2. Марковские цепи с доходами (платежами).
- •1.3.3. Рекуррентный алгоритм поиска решения мцп.
- •1.3.4. Итерационный алгоритм поиска решения мцп
- •1.3.5. Модели частоты рекламных воздействий
- •2. Модели планирования уровня жизни
- •2.1. Система моделей уровня жизни
- •2.1.1. Группы моделей уровня жизни
- •2.1.2. Индикаторы дифференциации доходов населения
- •3. Модели размещения производства
- •3.1. Задача размещения без ограничений
- •3.2. Задача размещения с ограничениями по мощности предприятий
- •3.3. Многостадийная задача размещения
- •4. Моделирование инвестиций
- •4.1. Элементы диверсификации
- •4.1. Модель одношагового распределения средств
- •2.1. Вычисление весов по мпс
- •2.2. Вычисление весов непосредственно по ранжировкам.
- •Литература
2.1.2. Индикаторы дифференциации доходов населения
Рассмотрим некоторые наиболее часто используемые математические индикаторы дифференциации доходов населения.
Коэффициент фондов (коэффициент
дифференциации доходов)
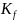 характеризует степень социального
расслоения населения по доходам. Он
определяется как
характеризует степень социального
расслоения населения по доходам. Он
определяется как
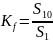
где
 - средний уровень доходов населения с
самыми высокими доходами;
- средний уровень доходов населения с
самыми высокими доходами;
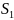 - средний уровень доходов населения с
самыми низкими доходами.
- средний уровень доходов населения с
самыми низкими доходами.
Децильный коэффициент дифференциации
доходов
 рассчитывается по сгруппированным
данным и показывает, во сколько раз
минимальные доходы 10% наиболее
обеспеченного населения (
рассчитывается по сгруппированным
данным и показывает, во сколько раз
минимальные доходы 10% наиболее
обеспеченного населения (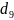 девятая дециль) превышают максимальные
доходы 10% наименее обеспеченной части
населения (
девятая дециль) превышают максимальные
доходы 10% наименее обеспеченной части
населения (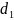 первая дециль):
первая дециль):
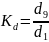


Размеры доходов





















Децили
2
3
4
5
6
1
7
8
9
0
10
Так по данным Росстата в 2004 году в России =15. Обычно этот показатель варьируется в интервале [5; 15].
Коэффициент Джини (коэффициент
концентрации доходов Лоренца)
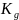 в отличие от двух предыдущих учитывает
не крайние группы шкалы доходов, а всю
шкалу.
в отличие от двух предыдущих учитывает
не крайние группы шкалы доходов, а всю
шкалу.
Для определения строится кривая Лоренца – накопленная сумма (или интеграл) от распределения, приведенного на предыдущем рисунке. По обеим осям откладываются %%.


100
Накопленный доход, %





S0

S1

Накопленная доля населения, %

100
0
Тогда
вычисляется как отношение площади между
диагональю и интегральной кривой к
площади треугольника:
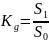 .
При равномерном распределении доходов
кривая Лоренца совпадет с диагональю,
тогда соответствующий коэффициент
Джини
=0.
.
При равномерном распределении доходов
кривая Лоренца совпадет с диагональю,
тогда соответствующий коэффициент
Джини
=0.
3. Модели размещения производства
Модели этого типа имеют несколько приложений в экономической практике, например:
размещения предприятий;
размещения складов;
размещения филиалов банка;
размещение пунктов обработки (приемки) и переработки отходов;
размещение поставщиками текущих партий товара в тех или иных из арендуемых складов.
3.1. Задача размещения без ограничений
Постановка задачи размещения предприятий, производящих некоторую однородную продукцию, имеет такой вид.
Задано множество пунктов возможного
размещения предприятий (или других
объектов размещения)
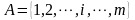 .
При этом известны затраты на размещение
предприятия в каждом из этих пунктов -
.
При этом известны затраты на размещение
предприятия в каждом из этих пунктов -
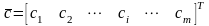 .
.
Известно множество потребителей -
 и соответствующие им объемы потребностей
в продукции на интервале времени
и соответствующие им объемы потребностей
в продукции на интервале времени
 .
Заданы и затраты на производство и
доставку продукции потребителю
.
Заданы и затраты на производство и
доставку продукции потребителю
 в пределах интервала времени
.
в пределах интервала времени
.
Задача размещения заключается в выборе множества пунктов размещения таким образом, чтобы суммарные издержки были минимальными. При этом подмножество предприятий из множества может быть любым в количестве от 1 до . Ограничения на мощность предприятий не накладываются.

Целевая функция имеет вид:
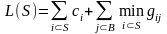
Отсюда критерий:
 .
.
Параметры и данные задачи можно представить и в табличном виде:
A |
ci |
B |
|||||
1 |
2 |
… |
j |
… |
n |
||
1 |
c1 |
g11 |
g12 |
… |
g1j |
… |
g1n |
2 |
c2 |
g21 |
g22 |
… |
g2j |
… |
g2n |
… |
… |
… |
… |
… |
… |
… |
… |
i |
ci |
gi1 |
gi2 |
… |
gij |
… |
gin |
… |
… |
… |
… |
… |
… |
… |
… |
m |
cm |
gm1 |
gm2 |
… |
gmj |
… |
gmn |
|
Σci |
min gi1 |
min gi2 |
… |
min gij |
… |
min g1j |
Первое слагаемое в ЦФ – это единовременные издержки, а второе – издержки производства (и логистики), где суммируются издержки по всем потребителям, а каждое слагаемое соответствует издержкам того предприятия из множества , для которого они минимальны.
Эта задача относится к комбинаторной оптимизации, для которых, как правило, нет общих методов решения, а часто используются эвристические процедуры. Если размерность задачи небольшая, то ее можно решить простым перебором вариантов.
Пример. Пусть имеется 3 места
размещения, т.е.
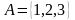 и 2 потребителя, т.е.
и 2 потребителя, т.е.
 .
Вектор единовременных затрат
.
Вектор единовременных затрат
 .
Матрица издержек производства и
логистики:
.
Матрица издержек производства и
логистики:
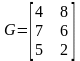 .
.
Решим эту задачу перебором вариантов. Все варианты подмножеств следующие:
 .
.
Вычислим все значения ЦФ:
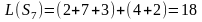
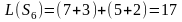
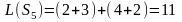


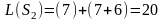

Наименьшим суммарным издержкам
соответствует вариант
 .
.
▲
