1.3.3. Рекуррентный алгоритм поиска решения мцп.

Рекуррентный алгоритм (РА) применяют для ограниченного числа шагов МЦП . Процедура выбора решений рассматривается как задача динамического программирования (ЗДП).

По аналогии с ЗДП оптимальный суммарный платеж , за оставшиеся t шагов, при перехода из -го состояния в j-ое ( ), при условии принятия решения , можно выразить через платеж за один шаг и оптимальный суммарный платеж за оставшиеся (t +1) шагов:

.

А поскольку процесс может перейти из -го состояния в любое j-ое с вероятностью , то условный (при условии выбора решения k) средний платеж:

.

Величина является целевой функцией (ЦФ) для выбора наилучшего k-го решения на t-ом шаге. Как и в ЗДП кроме решения ЦФ зависит и от текущего состояния i. Тогда, если платеж имеет смысл выигрыша, то уравнение Беллмана примет вид:

. (1)

А поскольку число шагов ограничено (N), то логично считать, что для (N+1)-го шага:

. (2)

Соотношение (1) представляет собой рекуррентное уравнение ЗДП, позволяющее найти оптимальное решение для каждого шага процесса. Поскольку в задаче (1)-(2) учитывается случайный характер выигрыша, её называют стохастической ЗДП.

Введя обозначение

, (3)

уравнение (1) для последнего шага, с учетом (2), можно записать в таком виде:

, (4)

а для остальных шагов:

, (5)

где - коэффициент дисконтирования.

Как и в ЗДП, условно-оптимальные решения отыскивается в обратном порядке (от последнего шага к начальному), а затем оптимальные – в прямом.

Алгоритм (4) - (5) можно применять и при нестационарных (изменяющихся по шагам) матрицах и .

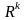1.3.4. Итерационный алгоритм поиска решения мцп

Есть два варианта алгоритма:

• полный перебор стратегий ;

• сокращенный перебор (алгоритм Р. Ховарда) с постепенным улучшением элементов вектора стратегий .

Решение будем искать в классе стационарных стратегий, т.е. таких векторов , которые остаются неизменными на протяжении всего процесса.

Рассмотрим, как можно построить целевую функцию.

Конкурирующие стратегии сравниваются между собой по величине среднего платежа за один шаг при большом количестве шагов ( ).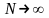

Определим средний платеж для -ой стратегии за один шаг в установившемся режиме, где , - полное количество возможных стратегий.

Для -ой стратегии из множества матриц можно составить одну рабочую и аналогично из матриц составить одну рабочую матрицу платежей .

Технология составления и состоит в том, что стратегия является ключом, для отбора строк из матриц и . Так первая строка в переносится из первой строки матрицы , вторая - из второй строки матрицы и т.д.

Аналогично конструируется и матрица . Таким образом, задача с K матрицами и K матрицами свелась к задаче с единственной матрицей и единственной матрицей , которые уже не зависят от решения k.

Средний платеж за один шаг при условии, что процесс находился в i-ом состоянии определится обычным усреднением:

.

Для вычисления безусловного среднего платежа необходимо определить вектор вероятностей состояний в установившемся режиме ( ). Тогда средний платеж за один шаг для фиксированной стационарной стратегии s в установившемся режиме определится так:

. (6)

Здесь можно принять в качестве целевой функции при выборе стратегии.

Тогда задача выбора оптимальной стратегии примет вид:

. (7)

Здесь неизвестным остается вектор . Из теории марковских процессов известно, что в установившемся режиме справедливо следующее матричное уравнение:

, (8)

где должно выполняться условие нормировки:

. (9)

Решение системы уравнений (8) и (9) позволяет получить значения координат вектора . Тогда в задаче (7) все элементы известны за исключением искомого аргумента s.

Пример. Рассмотрим, как можно построить матрицы и для типового примера.

Для и множество стратегий . Тогда, например, для стратегии

;

.

▲

Метод полного перебора стратегий состоит из следующих этапов:

1. Сформировать множество стратегий .

2. Для очередной стратегии s сформировать матрицы и .

3. Вычислить вектор вероятностей состояний в установившемся режиме , решив систему уравнений (8) и (9).

4. Вычислить средний платеж за один шаг по формуле (6).

5. Выбрать оптимальную стратегию по формуле (7), сравнив значения для всех стратегий.

Метод итерационного перебора стратегий (метод Р. Ховарда).

Этот метод основан на пошаговом улучшении стратегии , путем варьирования элементов (решений) на каждом шаге итерационного процесса и отбора таких значений в векторе , которые бы улучшали (или не ухудшали) выигрыш для каждого состояния .

Итерационный процесс прекращается, как только ни по одному элементу вектора стратегий нет улучшения.

Критерий выбора оптимальной стратегии такой же, как и в методе полного перебора: максимум безусловного среднего платежа за один шаг в установившемся режиме (т.е. при числе шагов процесса ).

Для любой стратегии из множества матриц и формируется одна матрица и одна . При этом МЦП с матрицей переходных вероятностей ведёт себя как обычная стационарная ЦМ.

В основе итерационного метода лежит уравнение Беллмана:

(10)

где, ось времени «развернута в обратную сторону», т.е. t означает число шагов, оставшихся до общей продолжительности процесса N.

В (10) от стратегии зависят лишь и , а не зависят. Здесь имеют смысл имеют смысл платежа при условии, что процесс находится в состоянии . В итерационном алгоритме их называют весовыми коэффициентами (ВК).

Схематически, метод состоит из двух чередующихся этапов:

• на 1-ом этапе - вычисляются ВК для стратегии ;

• на 2-ом этапе - улучшается стратегия варьированием решений для каждого состояния , в результате чего получается улучшенная стратегия .

Затем вновь повторяется 1-й этап и т.д. до тех пор, пока улучшенные стратегии на двух соседних шагах не будут отличаться.

Итерации можно начинать с любого из этапов.

На 1-ом этапе используются свойства уравнения (10) в установившемся режиме (при ), когда уже не будет зависеть от времени, а значит . С учетом этого (10) можно представить в таком виде:

, (11)

где и известны и однозначно определяются текущей стратегией , а не известны.

Следует решить систему уравнений (11) относительно неизвестных .

1-й этап называется этапом определения весовых коэффициентов (ВК).

На 2-ом этапе следует воспользоваться уравнением (10) для улучшения стратегии варьированием решений для каждого состояния , где и известны, а вычислены на 1-ом этапе. В (10) номер шага является номером итерации и - это ВК, вычисленные на предыдущей итерации. Т.е. в правой части (10) известны все элементы для фиксированной стратегии . Тогда, если изменять решения в , то значение левой части уравнения (10), имеющее смысл платежа для состояния , может служить показателем улучшения или ухудшения стратегии при варьировании элемента .

Таким образом, на данном (2-ом) этапе путем варьирования элементов текущей стратегии выбирается новая (улучшенная) стратегия, которая хотя бы по одному элементу вектора стратегий может оказаться лучше текущей. Новая стратегия становится текущей, и итерационный процесс переходит к 1-му этапу.

2-й этап называется этапом улучшения стратегии.

Этапы 1 и 2 повторяются до тех пор, пока процесс улучшения стратегий не прекратится, т.е. пока стратегии на двух соседних этапах не станут одинаковыми.

Приведенные алгоритмы поиска оптимальных стратегий МЦП успешно работают при условии, что характеристики процесса ( и ) известны. Однако обычно платежи многокритериальны и часто неизвестны. Для МЦП также возможно решение обратных задач, т.е. восстановление обобщенной матрицы и матрицы по наблюдениям.