1.3. Марковская модель управления затратами на рекламу.

1.3.1. Типовой пример.

Предприятие регулярно рекламирует свою продукцию в одном из трех печатных изданий:

1) в местной бесплатной газете рекламных объявлений;

2) в областной бесплатной газете рекламных объявлений;

3) в местной платной газете.

Недельный бюджет на рекламу в следующие 3 недели оценивается соответственно в 200, 900 и 300 денежных единиц. Предприятие оценивает недельный объем сбыта по следующей шкале:

• удовлетворительный (1);

• хороший (2);

• отличный (3).

Переходные вероятности между различными состояниями сбыта при различных вариантах рекламы и соответствующие доходы от сбыта приведены в табл. 1.

Таблица 1.

Выбор (вариант рекламы) k	Состояние (сбыт) i	Вероятности перехода			Доход от сбыта
		j=1	j=2	j=3	j=1	j=2	j=3
1	1	0.4	0.5	0.1	400	520	600
	2	0.1	0.7	0.2	300	400	700
	3	0.1	0.3	0.6	200	250	500
2	1	0.7	0.2	0.1	1000	1300	1600
	2	0.3	0.6	0.1	800	1000	1000
	3	0.1	0.2	0.7	600	700	1100
3	1	0.2	0.5	0.3	400	530	710
	2	0	0.7	0.3	350	450	800
	3	0	0.2	0.8	250	400	650

Например, если сбыт отличный (состояние 3) и выбран вариант рекламы 2 (областная бесплатная газета), то вероятности перехода на следующем шаге процесса в состояние 1 равна 0.1, в 2 – 0.2 и остаться в том же состоянии – 0.7. При этом соответствующие доходы от сбыта будут 600, 700 и 1100.

Поскольку процесс перехода на каждом шаге из одного состояния в другое является случайным и достоверно неизвестно, в каком состоянии будет сбыт на конкретном шаге, то оптимальный алгоритм управления должен носить характер стратегии с условными переходами, в виде конструкции «если-то». Для данного примера оптимальная стационарная стратегия может быть, например, такой:

,

где означает, что если процесс находится в 1-ом состоянии ( ), то следует выбрать 2-й вариант рекламы (принять решение 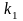). Аналогично если , то выбрать 3-й (решение 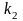), а если 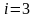, то надо выбрать 1-й (решение ).

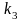Стратегия может быть и нестационарной – когда для каждого из 3-х шагов процесса строится свой вектор .

Количество шагов процесса может быть ограниченным и неограниченным.

Подобные задачи можно представить в виде марковских цепей с доходами (платежами).

1.3.2. Марковские цепи с доходами (платежами).

Случайным процессом называют функцию времени, принимающую случайные значения в каждый фиксированный момент времени.

Случайной последовательностью (цепью) называют случайный процесс с дискретными состояниями (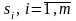 ) и временем ( ).

Если вероятность перехода ( ) из предыдущего в последующее состояние зависит только от предыдущего состояния, то такой процесс называется процессом без последействия. Случайную последовательность, обладающую таким свойством, обычно называют марковской цепью (МЦ) или цепью Маркова, а само это свойство - марковостью.

МЦ называется однородной (стационарной), если переходные вероятности 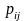не изменяются во времени.

МЦ считается заданной, если заданы: матрица вероятностей перехода (переходная матрица) процесса за один шаг и вектор вероятностей начальных состояний:

. (1)

Кроме матричной формы марковская цепь может быть представлена и в виде ориентированного взвешенного графа (см. рисунок для случая трех состояний),

где вершины соответствуют состояниям, а значения, указанные на дугах - вероятностям перехода из одного состояния в другое за один шаг процесса.

Важной характеристикой МЦ, является вектор предельных (финальных) вероятностей 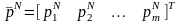, отражающий то, с какой вероятностью процесс окажется в том или ином состоянии через шагов.

Все свойства процесса, в том числе и 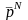, полностью определяются элементами (1), однако если возможность принимать некоторые решения, управляющие переходными вероятностями, то можно и воздействовать на . Такие МЦ называют управляемыми МЦ (УМЦ).

Управлением может быть, например, решение о внесении удобрений перед посевом сельхоз культур, что может повлиять на распределение вероятностей получения того или иного объема урожая.

К классу УМЦ относятся марковские цепи с платежами (МЦП). Их отличие от обычных МЦ в следующем:

1. На каждом ( - ом) шаге процесса перед переходом на следующей ((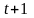 ) - й) шаг можно принять одно из множества решений: .

2. Для каждого варианта решения ( ) задана своя матрица условных вероятностей перехода за один шаг (МВП): 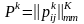. Здесь под условным имеется в виду следующее: « - это вероятность перехода в состояние на ( ) – ом шаге при условии, что на - ом шаге процесс находился в состоянии , если было принято решение ».

3. Для каждого варианта решения ( ) кроме МВП задана и матрица условных платежей за один шаг (МП): 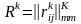, где - платеж (или доход) за один шаг при переходе в состояние на ( ) – ом шаге при условии, что на - ом шаге процесс находился в состояния и было принято решение .

Остальные элементы аналогичны обычным МЦ:

4. Множество состояний процесса .

5. Вектор вероятностей начальных состояний .

Пример. Приведенный выше типовой пример распределения рекламного бюджета на трех шагах можно представить следующими элементами:

▲

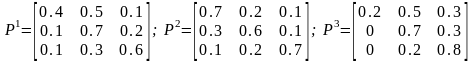
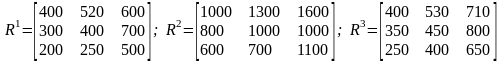
Таким образом, МЦП является моделью принятия решений, в которой:

• есть что выбирать - решения на каждом шаге;

• есть чем измерить качество выбираемого решения - платежами, накопленными за множество шагов или средние по всем шагам.

Существует два основных алгоритма поиска решений для МЦП:

• рекуррентный алгоритм, основанный на уравнении Р. Беллмана, где максимизируется накопленный выигрыш;

• итерационный алгоритм, где максимизируется средний выигрыш за один шаг.