
- •Часть 3
- •Содержание
- •1. Планирование маркетинговой политики. Методы оптимизации маркетинговых затрат (реклама, товародвижение и сбыт)
- •1.1. Основные элементы маркетинга.
- •1.2. Игровая модель управления конкурентоспособностью продукции.
- •1.2.1. Прямая задача.
- •1.2.2. Обратная задача.
- •1.3. Марковская модель управления затратами на рекламу.
- •1.3.1. Типовой пример.
- •1.3.2. Марковские цепи с доходами (платежами).
- •1.3.3. Рекуррентный алгоритм поиска решения мцп.
- •1.3.4. Итерационный алгоритм поиска решения мцп
- •1.3.5. Модели частоты рекламных воздействий
- •2. Модели планирования уровня жизни
- •2.1. Система моделей уровня жизни
- •2.1.1. Группы моделей уровня жизни
- •2.1.2. Индикаторы дифференциации доходов населения
- •3. Модели размещения производства
- •3.1. Задача размещения без ограничений
- •3.2. Задача размещения с ограничениями по мощности предприятий
- •3.3. Многостадийная задача размещения
- •4. Моделирование инвестиций
- •4.1. Элементы диверсификации
- •4.1. Модель одношагового распределения средств
- •2.1. Вычисление весов по мпс
- •2.2. Вычисление весов непосредственно по ранжировкам.
- •Литература
1.2.2. Обратная задача.
Пусть в дискретные моменты
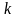 измерены смешанные стратегии игроков
измерены смешанные стратегии игроков
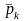 ,
,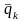 и выигрыш И1
и выигрыш И1
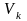 .
.
Построим алгоритм оценивания элементов матрицы в рекуррентной форме.
Уравнение измерений для произвольного (k-го) наблюдения, с учетом (1), примет вид:
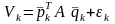 ,
(2)
,
(2)
откуда невязка
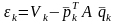 ,
(3)
,
(3)
где
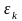 -
случайная составляющая (невязка),
обусловленная как неточностью измерений,
так и степенью соответствия модели игры
(матрицы А) реальной ситуации на
рынке.
-
случайная составляющая (невязка),
обусловленная как неточностью измерений,
так и степенью соответствия модели игры
(матрицы А) реальной ситуации на
рынке.
Для оценки элементов матрицы А воспользуемся методом наименьших квадратов (МНК). Согласно МНК критерий оптимальности оценок можно представить в следующем виде:
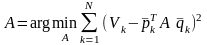 ,
(4)
,
(4)
где N – число наблюдений в выборке.
Приведем уравнение (2) к матричной форме.
Для этого представим скаляр
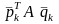 ,
или, что то же самое,
,
или, что то же самое,
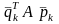 в несколько ином виде - переформируем
матрицу А в вектор
в несколько ином виде - переформируем
матрицу А в вектор
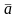 ,
для чего обозначим:
,
для чего обозначим:
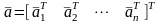 ,
(5)
,
(5)
где вектор
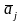 -
это
-й
столбец матрицы
,
тогда для всех
-
это
-й
столбец матрицы
,
тогда для всех
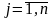 :
:
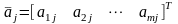 .
(6)
.
(6)
С учетом этих обозначений выразим 1-е слагаемое в (2):
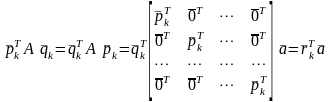 .
(7)
.
(7)
Здесь
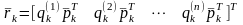 ,
(8)
,
(8)
где
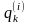 -
i-й компонент
вектора
,
-
i-й компонент
вектора
,
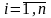 ,
,
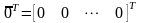 .
.
С учетом этих обозначений выигрыш на k-ом шаге (уравнение измерений (2)) примет вид:
 .
(9)
.
(9)
Для N шагов эти уравнения можно представить в векторной форме следующим образом:
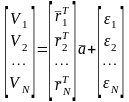 ,
(10)
,
(10)
или, иначе:
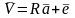 .
(11)
.
(11)
Отсюда сумму квадратов отклонений (невязок) можно представить в таком виде:
 .
(12)
.
(12)
Тогда критерий оптимальности оценок, аналогичный (4), но построенный для новой формы ЦФ (12), можно представить в следующем виде:
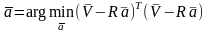 ,
(13)
,
(13)
Далее в соответствии с алгоритмом построения МНК-оценок по совокупности N измерений вектор платежей примет вид:
 ,
(14)
,
(14)
где нижний индекс отражает количество
измерений, по которым выполняется
оценивание, а «крышка» над
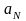 означает, что вычислена оценка
вектора платежей, а не истинные их
значения.
означает, что вычислена оценка
вектора платежей, а не истинные их
значения.
Обозначим:
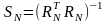 .
(15)
.
(15)
Представим алгоритм оценивания (14), (15) в рекуррентной форме:
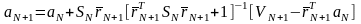 ,
(16)
,
(16)
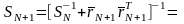
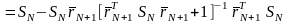 .
(17)
.
(17)
Алгоритм (16), (17) позволяет ЛПР накапливать
положительный опыт принятия решений
путем подстройки (уточнения) элементов
платежной матрицы по мере появления
новых наблюдений. А полученные на основе
этой матрицы решения (стратегия
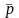 )
путем решения прямой АМИ будут
основаны на этом опыте и обеспечат
достижения желаемой конкурентоспособности
выпускаемой продукции.
)
путем решения прямой АМИ будут
основаны на этом опыте и обеспечат
достижения желаемой конкурентоспособности
выпускаемой продукции.
Пример. Рассмотрим случай, когда АМИ размерности mxn = 2х2:

Для нахождения решения прямой АМИ, т.е.
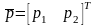 ,
,
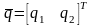 и цены игры
и цены игры
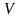 можно свести АМИ к паре задач линейного
программирования (ЗЛП) – прямой и
двойственной. Тогда прямая задача примет
вид:
можно свести АМИ к паре задач линейного
программирования (ЗЛП) – прямой и
двойственной. Тогда прямая задача примет
вид:
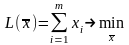
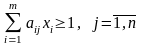
Решив эту задачу, получим и решение для И1:
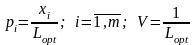
Двойственная задача примет вид:

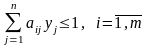
Решив эту задачу, получим и решение для И2:
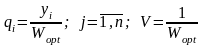
Для упрощения расчетов при решении обратной задачи элементы формул (16) и (17) для АМИ 2х2 (индексы номера шага опустим):
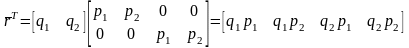
Введем обозначения:
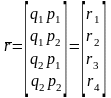 ;
;
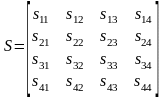
С учетом этого после преобразований формулы (16) по компонентам векторов можно представить в таком виде:

где номер итерации показан в скобках, i - номер компонента вектора;
 ,
где
,
где
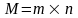
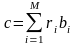
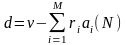
Формулу (17) можно представить в таком виде:
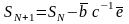
где компоненты вектора
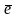 можно представить в таком виде:
можно представить в таком виде:
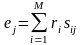 .
.
Приведенные соотношения позволяют вычислить все компоненты векторов и матриц для обратной задачи по текущим измерениям и затем прямой задачи по полученным оценкам матрицы АМИ не только 2х2, но и произвольной размерности.
