Лекция № 5. Обратная матрица. Матричный способ решения систем. Обратная матрица

Пусть А – квадратная матрица n – го порядка

Определение: Квадратная матрица называется невырожденной, если определитель не равен нулю: . В противном случае ( ) матрица А называется вырожденной.

Определение: Матрица называется союзной к матрице А, называется матрица

,

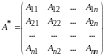где - алгебраические дополнения для элементов 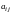матрицы А.

Определение: Матрица называется обратной для квадратной матрицы А, если , где Е – единичная матрица того же порядка, что и матрица А.

Следует запомнить, что понятие обратной матрицы вводится только для квадратной матрицы, причем невырожденной, т. е. определитель ее отличен от нуля.

Пусть - квадратная матрица и невырожденная

Пусть - матрица, союзная к матрице А.

Пусть - присоединенная матрица для матрицы А. Матрица является транспонированной по отношению к матрице .

Все элементы матрицы делим на - определитель матрицы А.

.

Пример 1. Найти матрицу, обратную матрице

Решение

Матрица А – квадратная.

Найдем .

Так как , то матрица А – невырожденная, и, следовательно, существует обратная ей матрица.

Вычисляем алгебраические дополнения:

Составляем матрицу 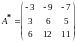. Транспонируем матрицу , получаем .

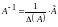
Матричный способ решения систем

Пусть дана система n – линейных уравнений с n – неизвестными. Система неоднородная.

.

- матричное уравнение системы, где

,

Если система записана в форме матричного уравнения и матрица А системы невырожденная, то решение матричного уравнения находим по формуле:

.

Следует запомнить.

Чтобы решить систему линейных уравнений, достаточно:

1. Составить матрицу , обратную матрице А, состоящей из коэффициентов при неизвестных системы;

2. Умножить матрицу В, состоящую из столбца свободных членов, слева на матрицу .

Пример 2. Решить матричным способом систему уравнений

Решение

В матричной форме эта система запишется в виде .

Здесь , , .

Найдем . Имеем .

Вычислим алгебраические дополнения для матрицы А.

, , ,

, , ,

, , .

, тогда

и

Ответ: ; ; .