Лекция № 4. Метод Гаусса. Решение систем линейных уравнений методом Гаусса.
Рассмотрим систему m-линейных уравнений c n-неизвестными
(1)
Теорема: Если какое-либо уравнение системы умножить на произвольное число и прибавить это произведение к другому уравнению системы, оставив при этом неизменными все остальные уравнения системы, включая то, которое умножалось на число, то получим систему, равносильную исходной.
Составим расширенную
матрицу системы (1)
.
Строки матрицы соответствуют уравнениям системы. Умножение уравнения на число и сложение этого произведения с другим, эквивалентно умножению строки матрицы на это число и почленному сложению произведения с другой строкой матрицы. Таким образом, работа с уравнениями заменяется работой со строками матрицы.
Этапы решения:
I
Этап: прямой ход заключается в том,
что система (1) приводится к ступенчатому
виду:
, (2)
в частности, к
треугольному виду:
. (3)
Следует запомнить.
Другими словами, если данная система уравнений (1) после выполнения ряда элементарных преобразований приводится к треугольному виду, то это означает, что система (1) является совместной и определенной.
Замечание.
Если в процессе
приведения системы (1) к ступенчатому
виду появляется уравнение вида
,
то система несовместна.
II этап: обратный ход заключается в решении ступенчатой (треугольной) системы.
Двигаясь снизу
вверх по уравнениям системы (3) находим
;
затем, подставляя значение
в предыдущее уравнение, находим
и т. д..
Если система (1)
после элементарных преобразований
приводится к ступенчатой системе (2),
то, перенеся члены с неизвестными
,
в правую часть, получим систему вида
(4).
. (4)
Придаем неизвестным
,
произвольные значения
и получаем треугольную систему.
(5)
Если система (1) после элементарных преобразований приводится к ступенчатой системе (2), то, перенеся члены с неизвестными , в правую часть, получим систему вида (4).
Замечание.
-
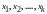свободные неизвестные.
-
базисные неизвестные.
Из системы (5),
поднимаясь снизу вверх, найдем
последовательно все остальные
неизвестные
.
Замечание.
Так как числа могут иметь различные значения, то исходная система (1) имеет бесчисленное множество решений.
Однородная система m линейных уравнений с n – неизвестными.
- однородная СЛАУ.
(6)
Однородная система
всегда совместна, т. к.
,
,
…,
образуют решение системы. Это решение
называется нулевым.
Нулевое решение будет единственным решением системы (6). Либо помимо нулевого решения должно существовать бесчисленное множество ненулевых решений.
Задачи
Пример
1. Решить систему уравнений
Решение
Составляем расширенную матрицу системы и приводим ее к ступенчатому виду.
~
~
~
Система несовместна.
Пример
2. Решить систему уравнений
Решение
Составляем расширенную матрицу системы и приводим ее к ступенчатому виду.
~
~
~
~
Система
совместна и определена. Двигаясь снизу
вверх по уравнениям системы
,
находим
,
;
,
.
Таким
образом, получаем единственное решение
системы
.
Пример
3. Решить систему уравнений
.
Решение
Составляем расширенную матрицу системы и приводим ее к ступенчатому виду.
~
~
~
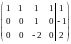Так как после преобразований число уравнений меньше числа неизвестных, то система неопределена.
Для решения необходимо определить базисные и свободные неизвестные.
Таким образом,
и
- базисные неизвестные, а
и
- свободные неизвестные системы.
.
.
Отсюда
.
Общее
решение системы
.
Положив, например,
,
,
получаем одно из частных решений:
,
,
,
.
Придавая свободным неизвестным произвольные значения, найдем различные решения системы.