Примеры решения типовых задач

Пример 1. Найти область сходимости функционального ряда

.

Решение. При х=0 ряд принимает вид , его частичная сумма , и, по определению суммы ряда .

Пусть – фиксированное число, . Исследуем сходимость получившегося числового ряда по интегральному признаку Коши: . Интеграл расходится при всех фиксированных значениях , следовательно, расходится при всех и ряд . Данный ряд получается из вспомогательного ряда умножением на число , что не меняет сходимости ряда. Таким образом, область сходимости данного ряда состоит из одной точки .

Пример 2. Найти область сходимости функционального ряда

.

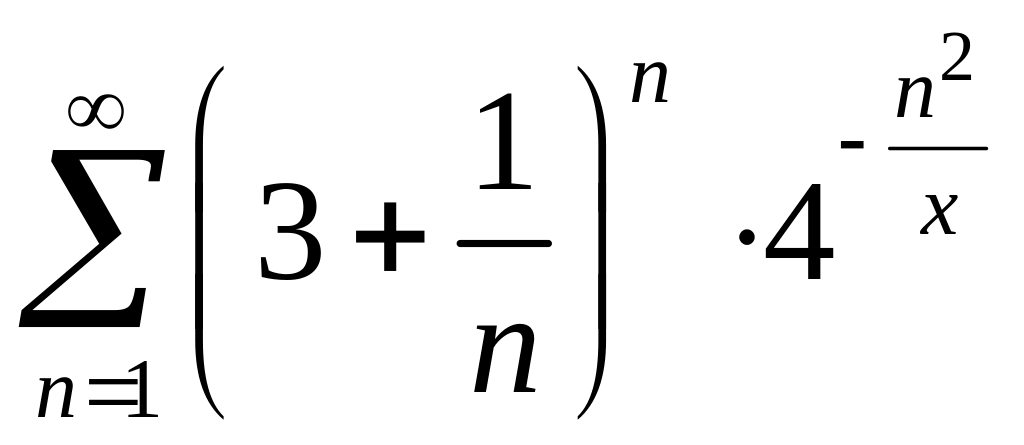Решение. Из условия следует, что . Пусть – фиксированное число, отличное от нуля. Исследуем сходимость получившегося числового ряда по радикальному признаку Коши:

.

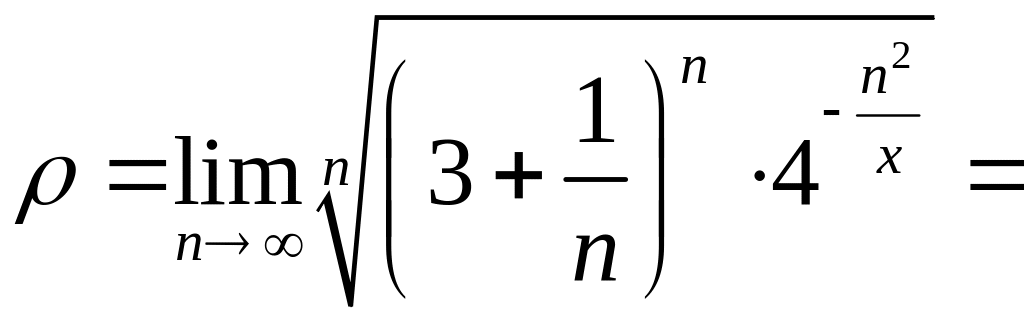
Итак, при и ряд расходится, при и ряд сходится. Поэтому область сходимости ряда .

Пример 3. Исследовать на равномерную сходимость ряд 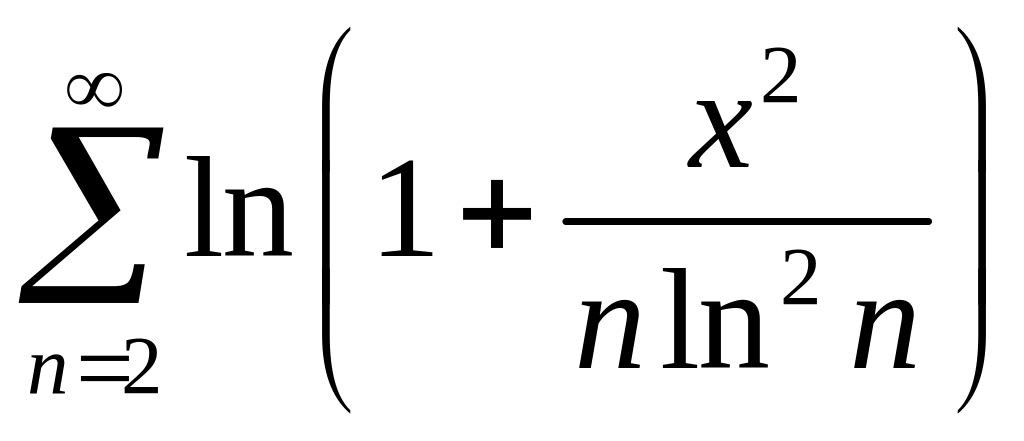на .

Решение. На справедливо

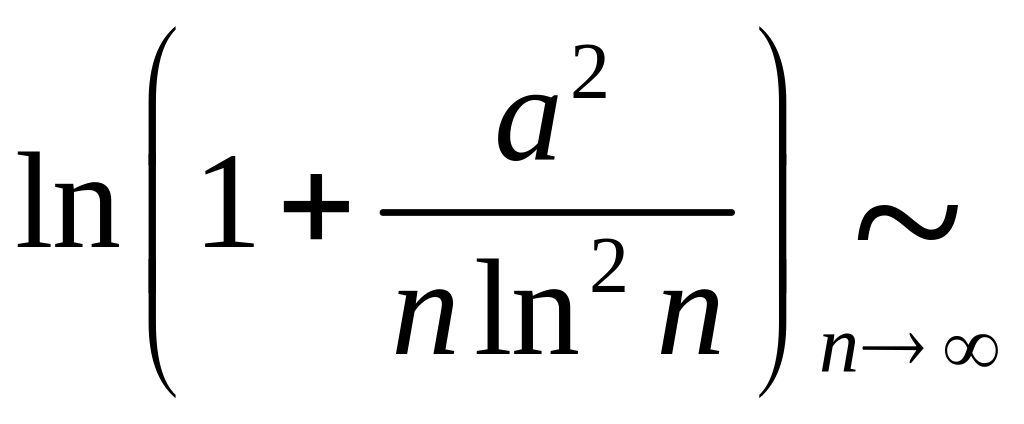
при , а 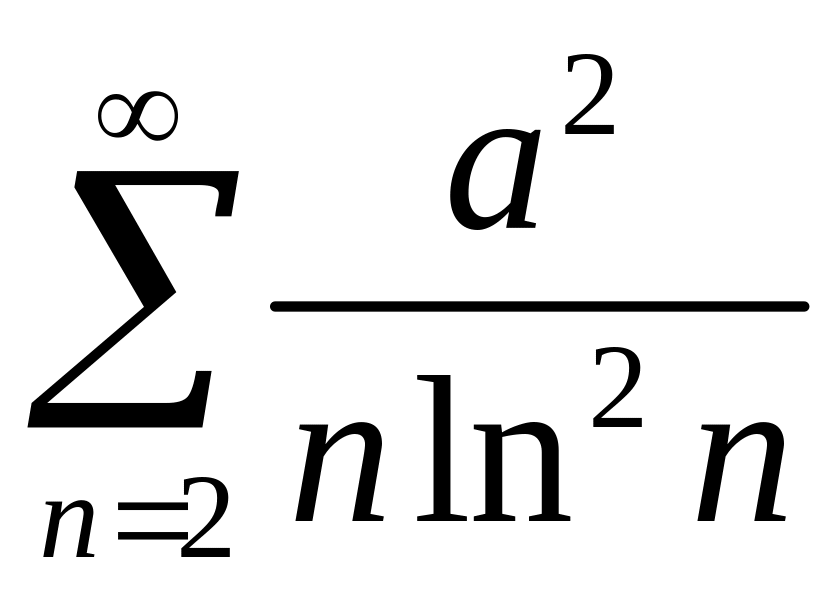сходится (по интегральному признаку). Тогда сходится (по теореме сравнения). Значит, по признаку Вейерштрасса данный ряд сходится равномерно на .

Пример 4. Исследовать на равномерную сходимость ряд

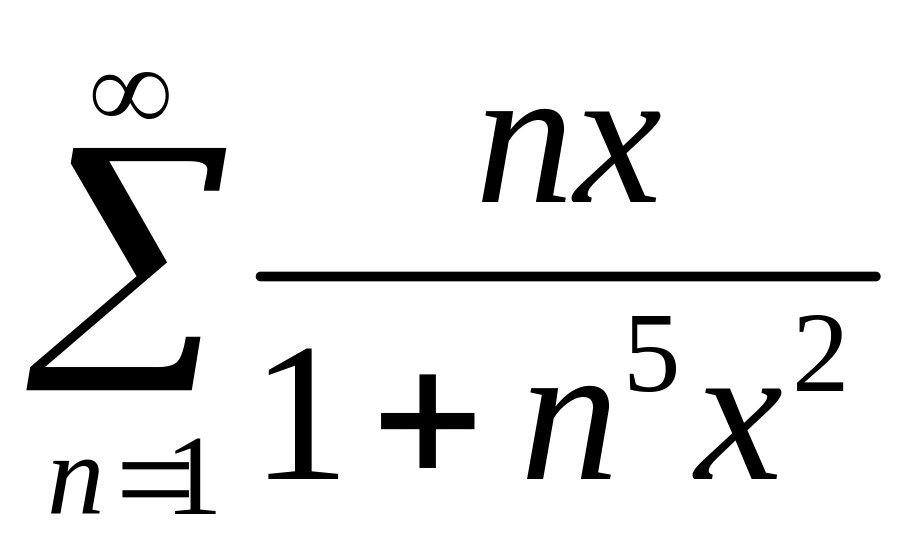для .

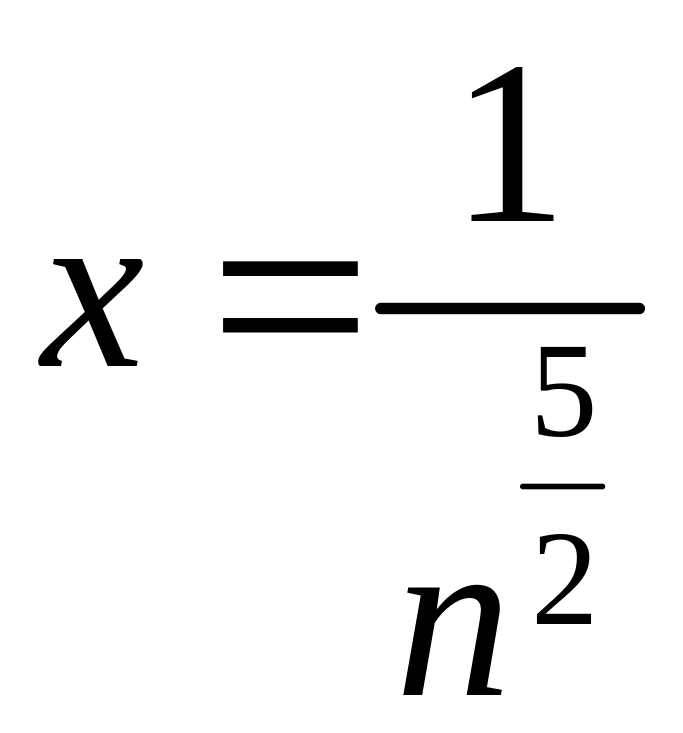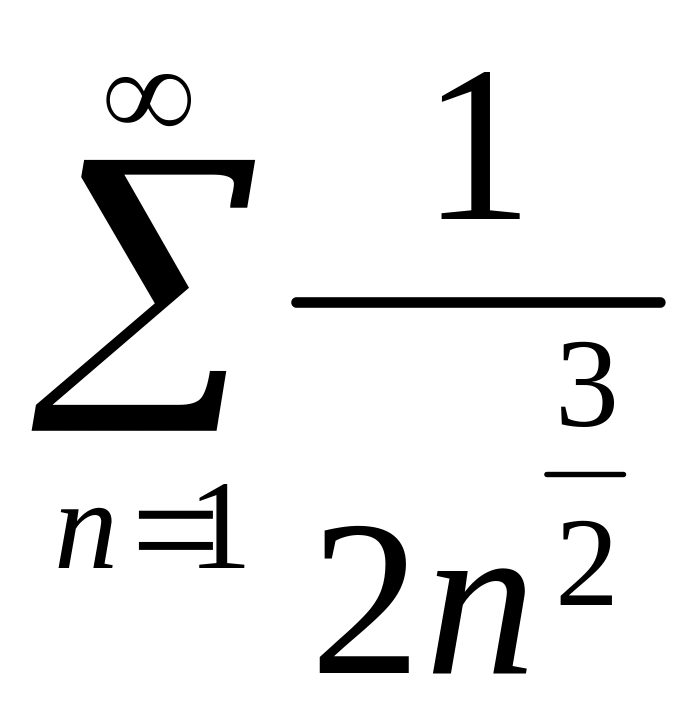Решение. при . Значит, , но сходится. Тогда по признаку Вейерштрасса данный ряд сходится равномерно на всей числовой оси и абсолютно.

Задания для самостоятельной работы

n10.10. Найти область сходимости степенного ряда:

а) ;	б) ;
в) ;	г) ;
д) ;	е) ;
ж) ;	з) .

Ответы

10.4. Степенные ряды

Краткие теоретические сведения

Определение. Функциональный ряд, членами которого являются степенные функции, называется степенным рядом .

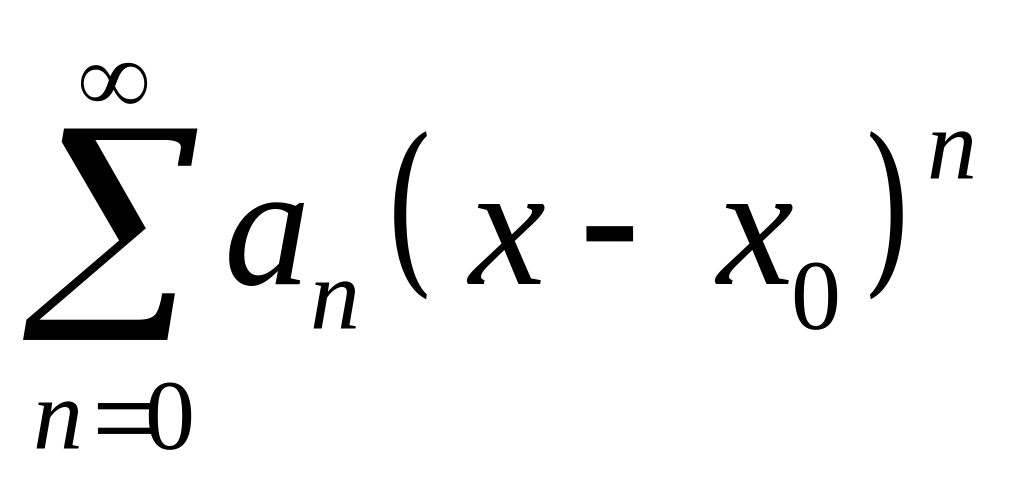Он является частным случаем функционального ряда, поэтому все теоремы и свойства, справедливые для функциональных рядов, справедливы и для степенных рядов.

Для каждого степенного ряда существует интервал сходимости E={x, }, где – радиус сходимости, который в случае может быть вычислен по формулам 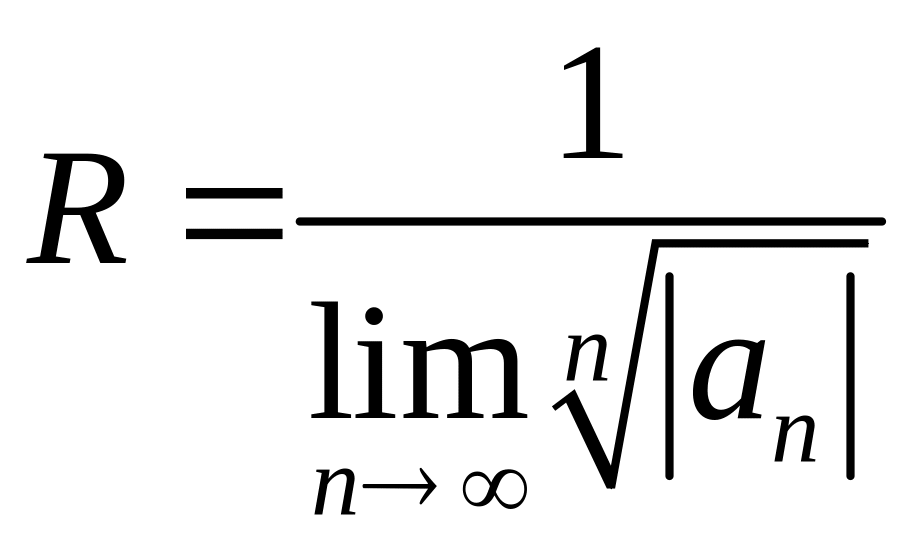, если эти пределы существуют (конечные или бесконечные). Область сходимости степенного ряда может включать, наряду с интервалом сходимости Е этого ряда, только концы интервала x=x₀ - R, x=x₀+ R. Для выяснения поведения степенного ряда на концах интервала сходимости надо исследовать числовые ряды, получаемые при подстановке этих точек в ряд .

Теорема. На всяком отрезке, целиком принадлежащим интервалу сходимости, степенной ряд сходится равномерно.

Следствие. Степенные ряды можно почленно интегрировать и дифференцировать на любом отрезке, принадлежащем интервалу сходимости.

Примеры решения типовых задач

Пример 1. Найти область сходимости степенного ряда

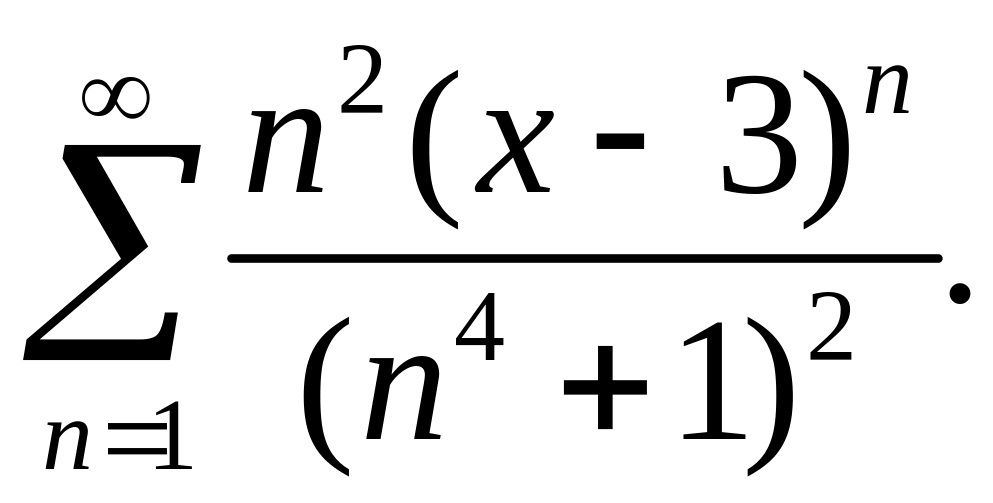
Решение. Интервал сходимости можно найти, применяя признак Даламбера или Коши к ряду, составленному из абсолютных величин членов исходного ряда. Здесь

Вычислим предел

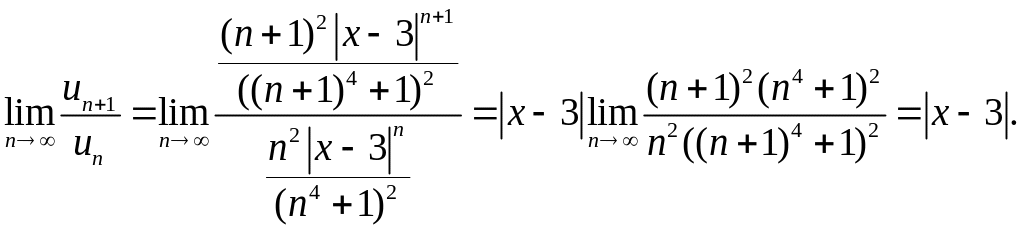
По признаку Даламбера для сходимости ряда предел должен быть меньше 1.

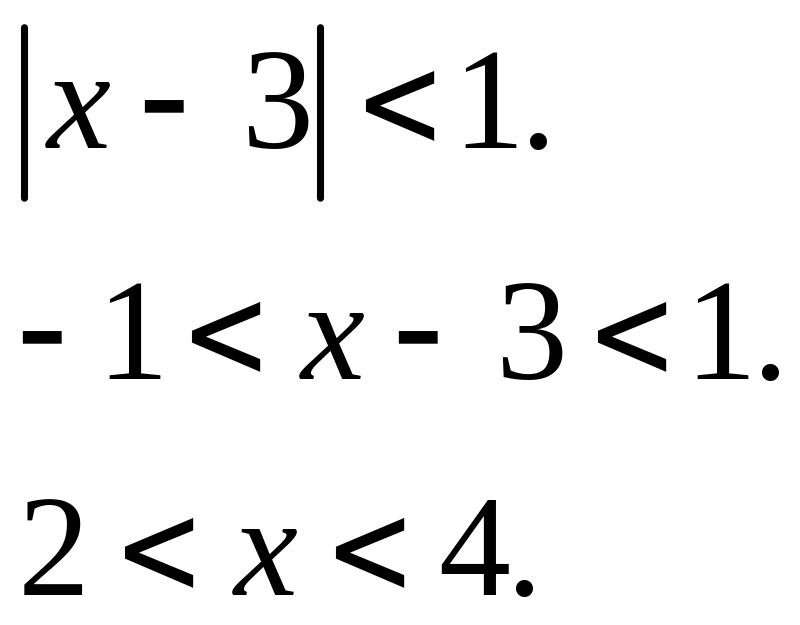
Исследуем сходимость ряда на концах промежутка .

Если x = 4, то получим ряд . Он сходится, так как этот ряд ведет себя как ряд .

Если x = 2, то получим ряд 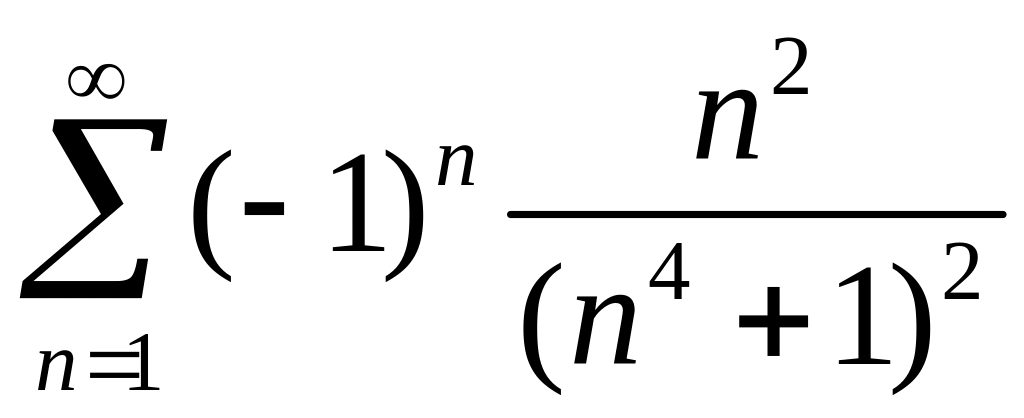. Он сходится и притом абсолютно, так как сходится ряд из абсолютных величин его членов.

Окончательно получим, что область сходимости исследуемого ряда отрезок [2; 4].

Пример 2. Найти область сходимости функционального ряда

.

Решение. Данный ряд является степеннным. Он содержит только четные степени , поэтому искать радиус интервала сходимости по соответствующей формуле нельзя. Зафиксируем и исследуем сходимость получившегося числового ряда по признаку Даламбера.

.

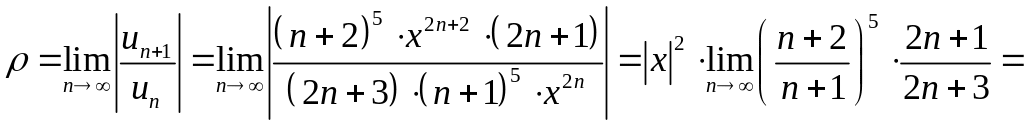
Ряд сходится, если , т.е. , откуда .

Исследуем поведение ряда на концах интервала сходимости.

При функциональный ряд принимает вид

= .

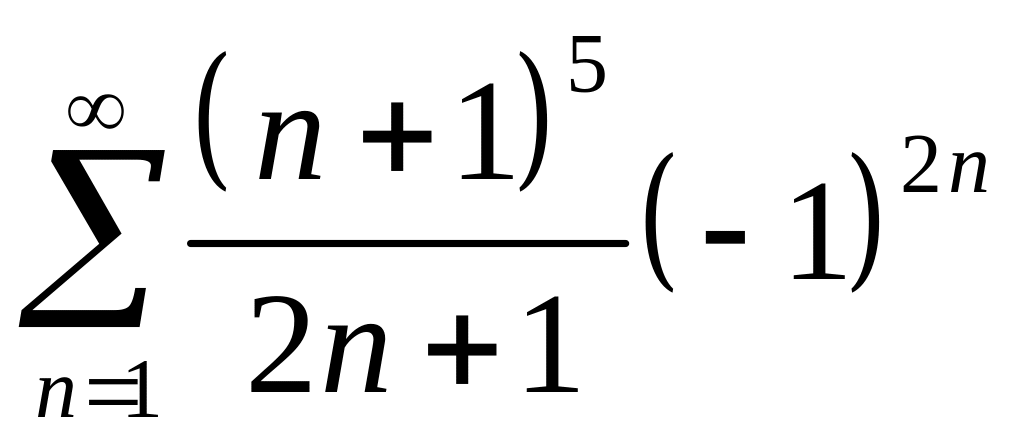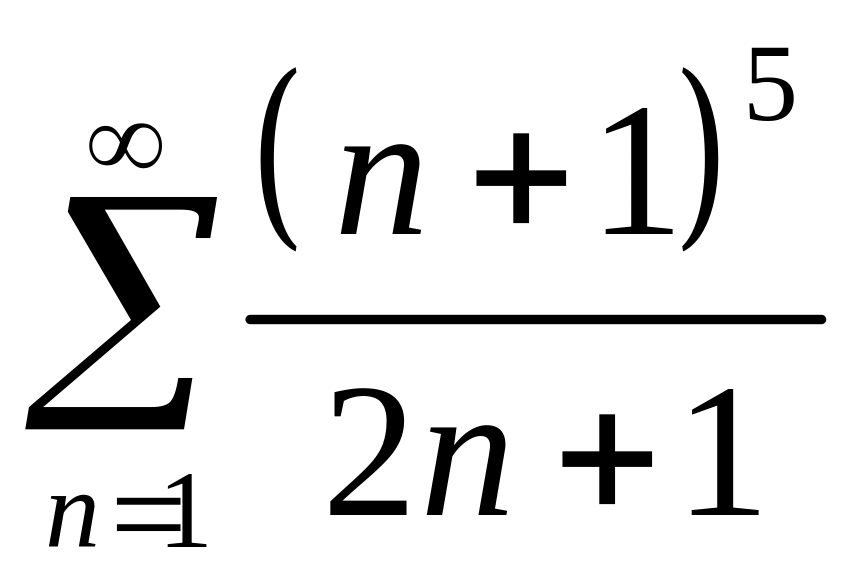Этот числовой ряд расходится, так как не выполняется необходимый признак сходимости: 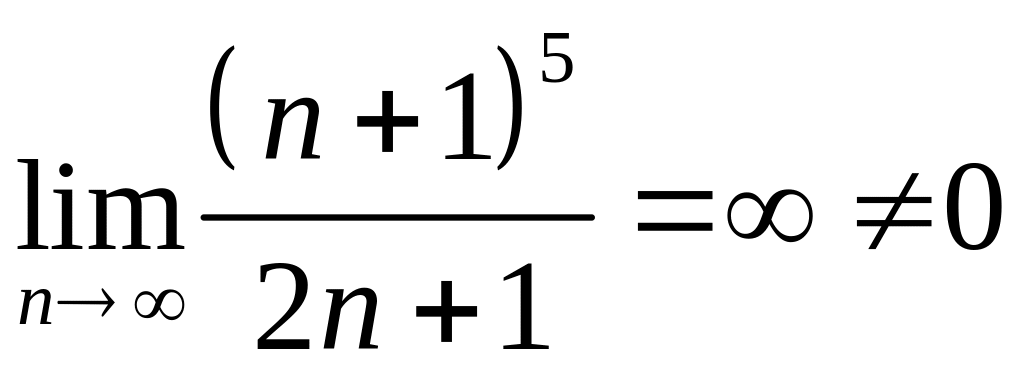. Поэтому область сходимости данного ряда .

Пример 3. Найти сумму ряда .

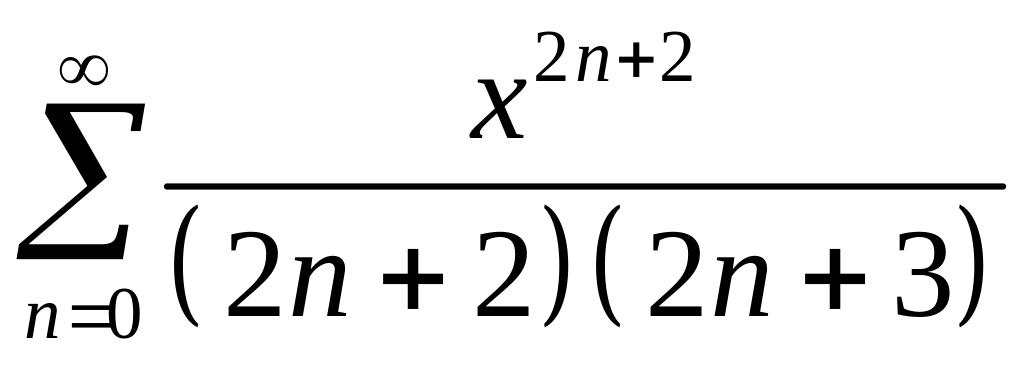Решение. Представим коэффициент перед переменной в виде суммы простейших дробей 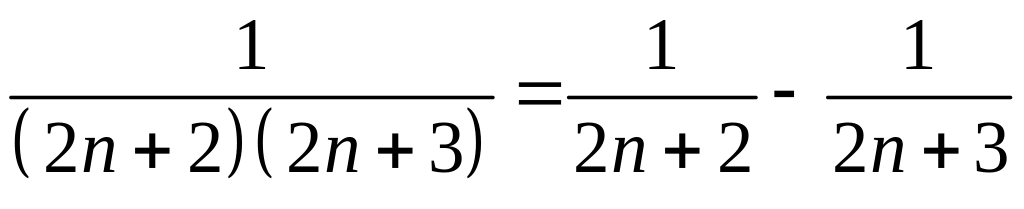. Теперь данный ряд можно представить в виде алгебраической суммы двух рядов:

. Степенные ряды почленно интегрируются, поэтому

= ,

при При замене ряда функцией воспользовались известной формулой – суммы бесконечно убывающей прогрессии , .

= =

.

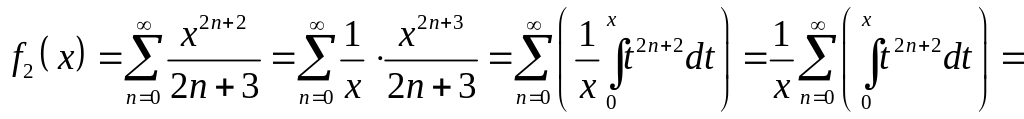
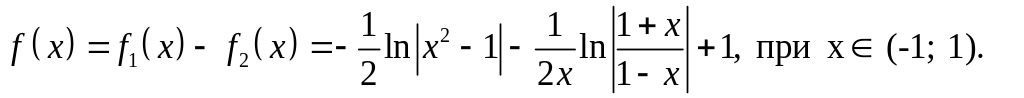
Пример 4. Найти сумму ряда .

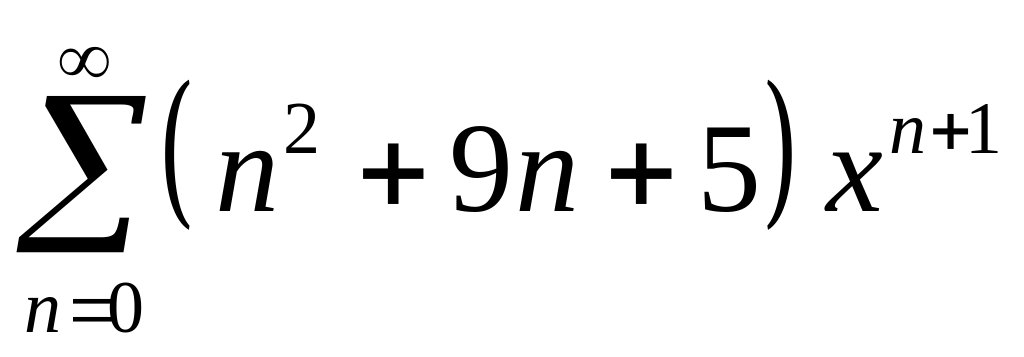Решение. Представим коэффициент перед переменной в следующем виде . Тогда данная сумма распадается на три:

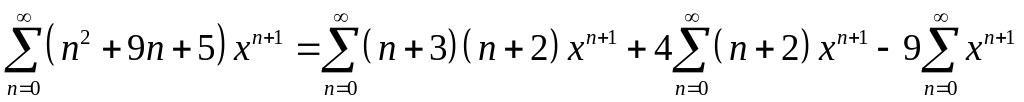
Степенные ряды можно почленно дифференцировать, поэтому

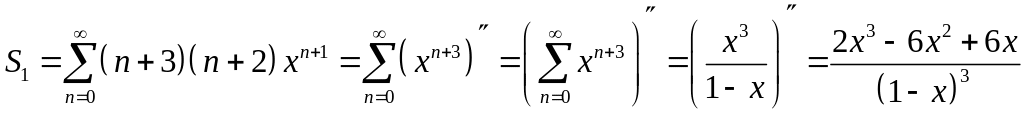при .

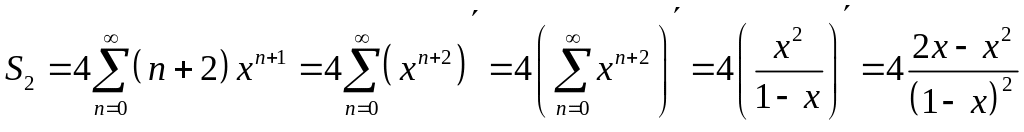
при .

.

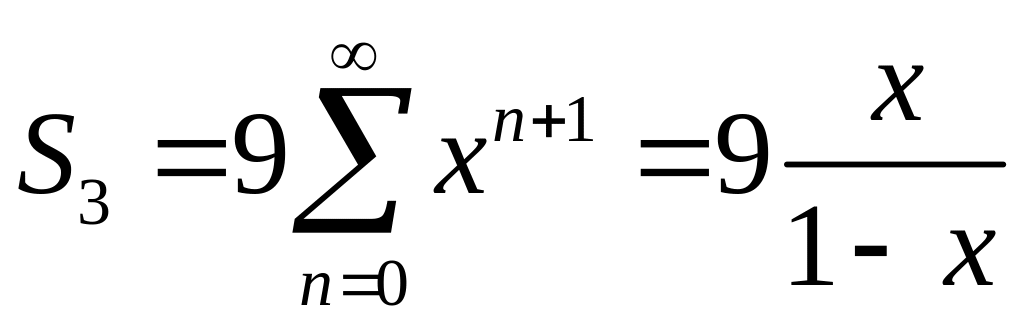При замене суммы функцией воспользовались известной формулой суммы бесконечно убывающей геометрической прогресси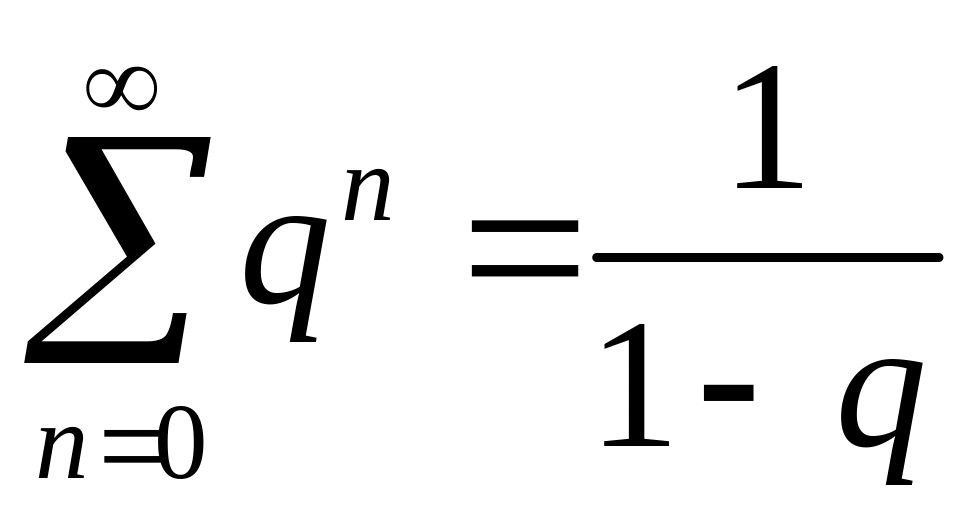и: при .

В итоге:

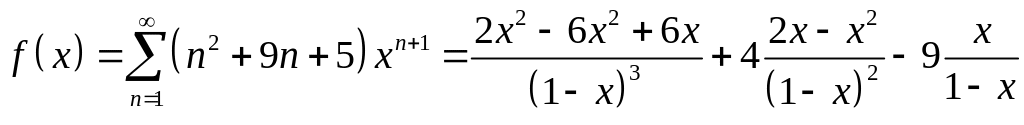
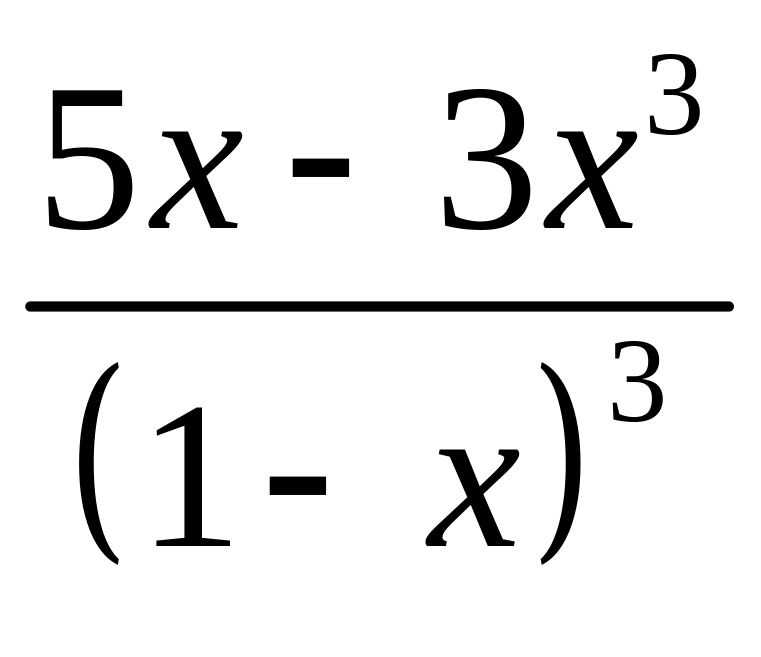= при n (-1; 1).
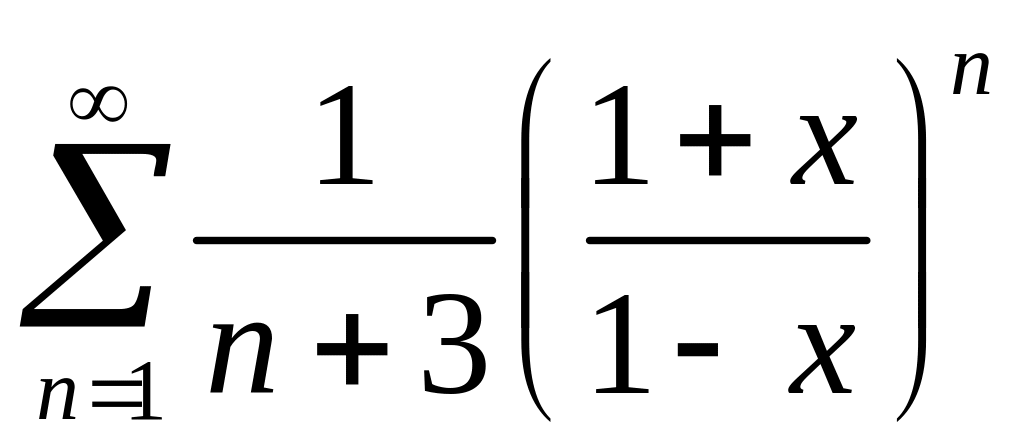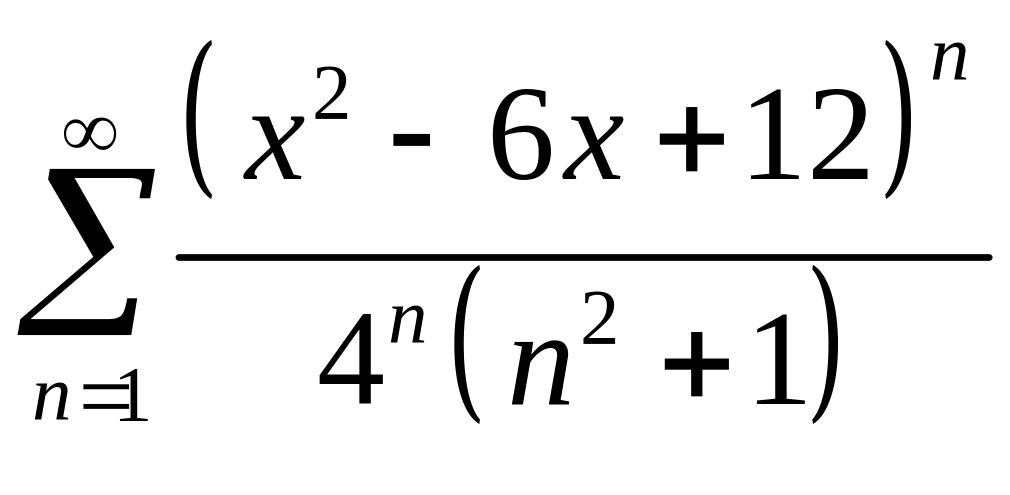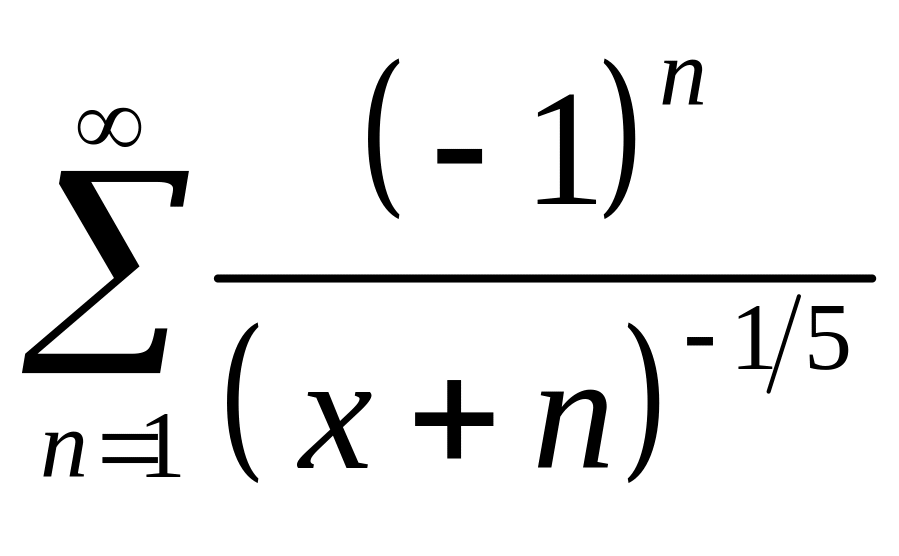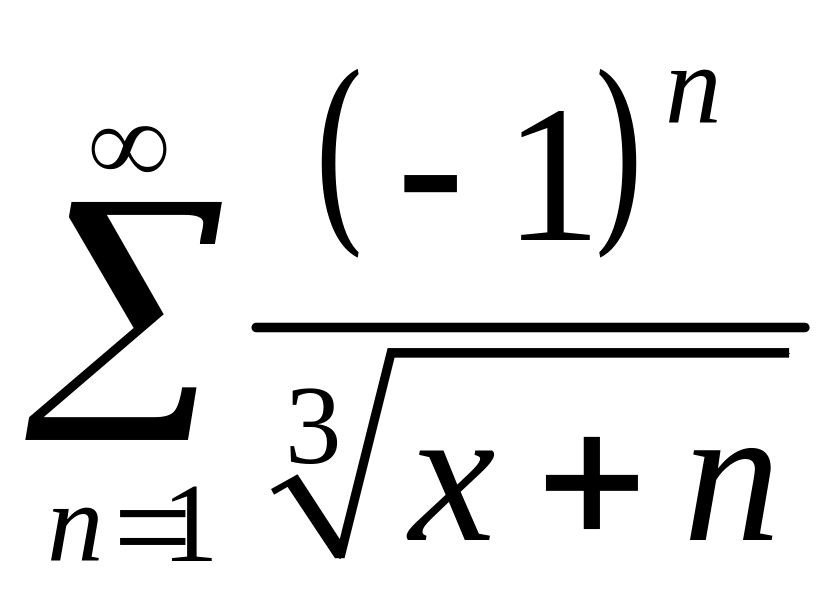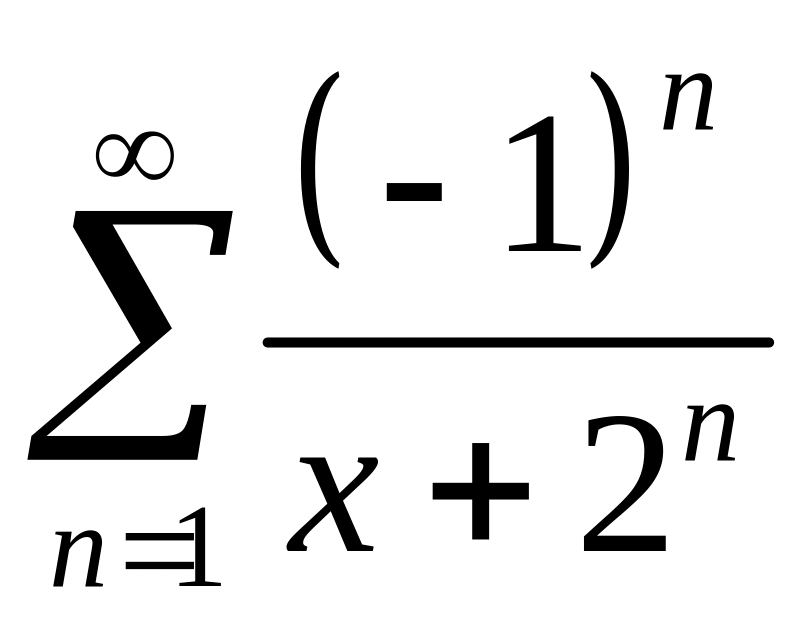