Вопрос №23: Действительная и фиктивная (приведенная) скорости потока в зернистом слое. Каково соотношение между ними?

Зернистый слой может быть монодисперсным – из частиц одинакового размера или полидисперсным – из частиц различных размеров. Режим движения потока через такие слои зависит от многих факторов. На распределение скоростей, прежде всего, влияют физические свойства потока и физические и геометрические характеристики слоя, т.е. его структура. Зернистый слой характеризуется:

- пористостью слоя, которая представляет собой отношение объема пустот в слое к общему объему слоя

,

где V – общий объем слоя; V_ч – объем, занимаемый частицами слоя; V_св – свободный объем слоя.

Отсюда, объем, занимаемый частицами и свободный и ;

- удельной поверхностью (м²/м³ или см²/г), т.е. отношением площади поверхности всех частиц к объему, занимаемому слоем или его массе;

- эквивалентным диаметром каналов d_э и их извилистостью α_к;

- скоростью витания частиц v_вит.

Потери давления при движении жидкости через зернистый слой могут быть подсчитаны по формуле, аналогичной потерям давления на трение в трубопроводах, т.е. по формуле Дарси-Вейсбаха:, (4.15)

где λ – коэффициент, отражающий влияние не только сопротивления трения, но и дополнительных местных сопротивлений межзерновых каналов, т.е. λ является общим коэффициентом сопротивления; d_э – эквивалентный диаметр каналов зернистого слоя; l_к – длина каналов.

Для определения эквивалентного диаметра необходимо знать площадь живого сечения потока жидкости и смоченный периметр.

Если поперечное сечение слоя (аппарата) S, а высота зернистого слоя h, то объем слоя V = S∙h, а объем каналов (свободный объем) .

Длина каналов с учетом их извилистости будет в α_к раз больше высоты слоя, т.е. l_к = α_к∙h. Тогда живое сечение потока, равное свободному сечению слоя, будет равно

.

Общая поверхность каналов равна произведению удельной поверхности частиц в м²/м³ на объем слоя V = S∙h

.

Периметр каналов (периметр свободного сечения) может быть вычислен делением общей поверхности каналов на их длину.

Тогда эквивалентный диаметр каналов зернистого слоя, (4.16) т.е. эквивалентный диаметр равен учетверенной порозности слоя, деленной на удельную поверхность.

Так как определить действительную скорость жидкости (газа) в каналах очень трудно, то в расчеты вводят так называемую фиктивную (среднюю) скорость v_о, равную отношению объемного расхода жидкости ко всей площади поперечного сечения слоя. При подсчете v_о пренебрегают кривизной каналов, т.е. полагают α_к = 1. Если извилистость каналов не учитывать, то их длина l_к будет равна высоте слоя l_к = h.

Тогда общее сечение каналов составит

и объемный расход жидкости будет равен , где v – действительная скорость.

Выразим объемный расход через фиктивную скорость жидкости. По определению фиктивной скорости объемный расход будет равен произведению всей площади поперечного сечения слоя S на v_о, т.е. V₀ = S· v_о. Приравнивая объемные расходы жидкости, выраженные через действительную и фиктивную скорости, получим

= , откуда , где v_о – фиктивная скорость.

Отсюда действительная скорость . (4.17)

ВОПРОС №24: Охарактеризовать состояние зернистого слоя в зависимости от скорости восходящего потока газа или жидкости. Сопроводите ответ графическими изображениями зависимостей потери давления и высоты слоя от скорости потока.

Установлено, что перевод зернистого слоя в псевдоожиженное (кипящее) состояние позволяет интенсифицировать многие процессы химической технологии (адсорбции, сушки, теплообмена и т.п.), а также создать условия для перемещения и смешивания сыпучих материалов. При этом размер частиц должен быть небольшим, что приводит к увеличению поверхности их контакта с жидкостью или газом (а это очень важно для ускорения процессов тепло- и массообмена) при сравнительно невысоком гидравлическом сопротивлении. Скорость процессов тепло- и массообмена повышается ещё и потому, что в условиях псевдоожижения практически вся поверхность всех частиц омывается потоком, причём при значительных скоростях. Рассмотрим три основных состояния слоя зернистого материала в зависимости от скорости жидкости или газа (рис. 6-16).

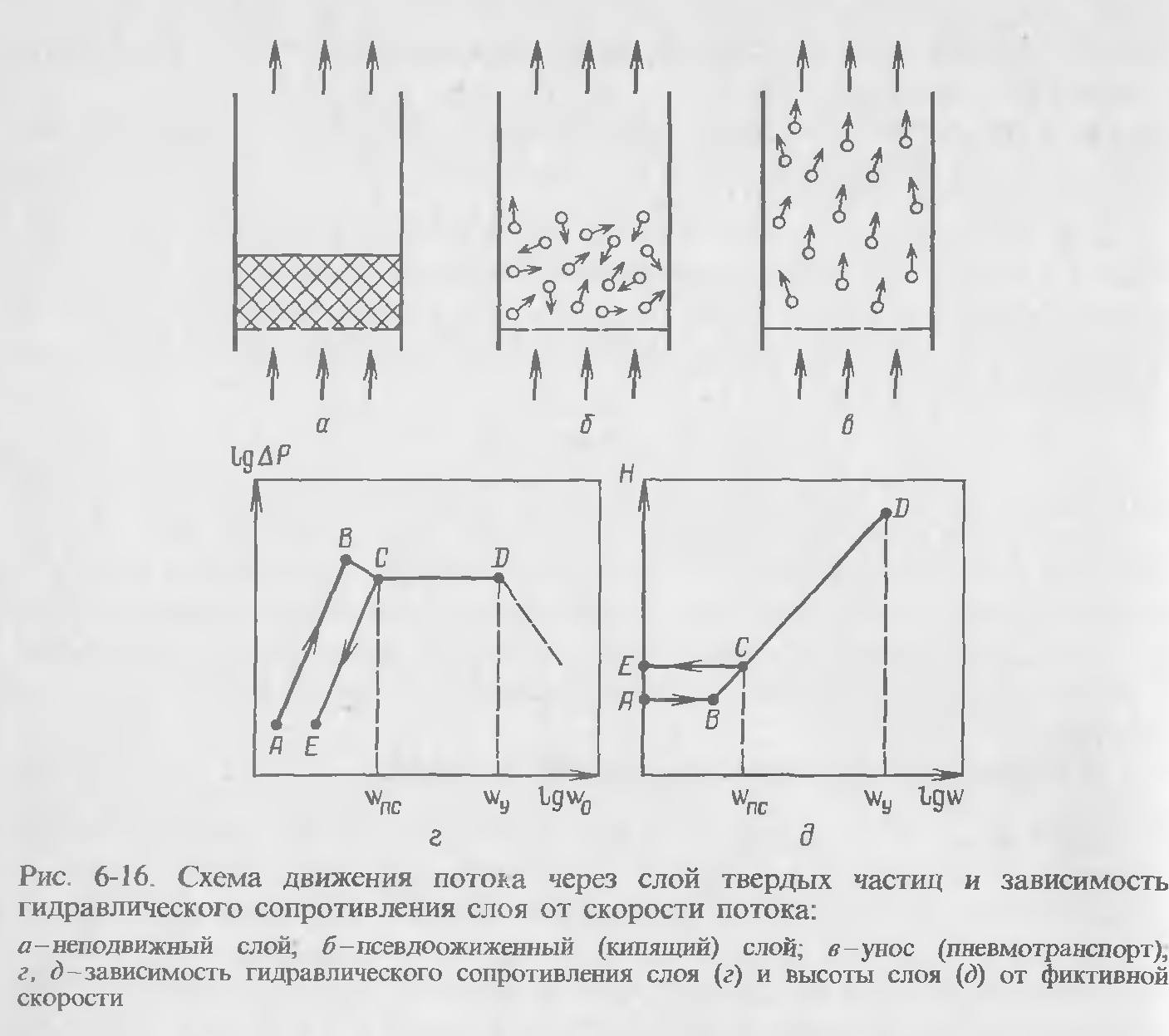
При скорости w₀ потока ниже некоторого критического значения w_пс (скорости псевдоожижения) слой зернистого материала (рис. 6-16, а) находится в неподвижном состоянии, его гидравлическое сопротивление увеличивается (линия ABC на рис. 6-16, г), а порозность ε и высота Н практически неизменны (линия ABC на рис. 6-16, д). По достижении некоторой критической скорости w_пс , соответствующей точке С на рис. 6-16, г, д, гидравлическое сопротивление зернистого слоя становится равным его весу G_т , отнесенному к площади сечения S аппарата, т.е.

∆р= G_т / S.

Но величину G_т можно выразить следующим образом: Gт = SH(1-ε)(ρ_т-ρ)g.

Тогда ∆р=H(1-ε)(ρ_т-ρ)g.

Слой приобретает текучесть, частицы слоя интенсивно перемещаются в потоке в различных направлениях (рис. 6-16, б), в нём наблюдается проскакивание газовых пузырей, а на его свободной поверхности появляются волны и всплески; порозность и высота слоя увеличиваются (рис. 6-16, д). В этом состоянии слой напоминает кипящую жидкость, благодаря чему он был назван псевдоожиженным (или кипящим). Скорость w_пс называют скоростью начала псевдоожижения. В этих условиях слой ещё имеет довольно четкую верхнюю границу раздела с потоком, прошедшим слой. Линия BC на рис. 6-16, г, д отражает влияние сил сцепления между частицами.

При дальнейшем увеличении скорости потока до некоторого критического значения w_у частицы перемещаются интенсивней, порозность и высота слоя продолжают возрастать при практически постоянном гидравлическом сопротивлении (линия CD на рис. 6-16, г, д). При скоростях, превышающих новую критическую скорость w_у , происходят разрушение псевдоожиженного слоя и вынос частиц потоком (рис. 6-16,в). Это явления массового уноса частиц называют гидро- или пневмотранспортом и используют в технике для перемещения сыпучих материалов. Скорость w_у , соответствующую началу массового уноса частиц, называют скоростью уноса, или скоростью свободного витания частиц. Последнее название обусловлено тем, что при w₀ = w_у порозность слоя настолько велика (ε≈1), что частицы движутся практически независимо друг от друга, свободно витают, не осаждаясь и не уносясь потоком, т.е. в этом случае (т. D на рис. 6-16, г, д) вес частицы уравновешивается силой сопротивления, возникающей при обтекании частицы потоком. Поэтому скорость w_у можно определить, так же как и скорость осаждения.

При снижении скорости потока после псевдоожижения слоя оказывается, что зависимость гидравлического сопротивления от скорости (рис. 6-16,г) выражается линией CE, а не BA. Этот гистерезис объясняется тем, что после псевдоожижения порозность слоя становится большей, чем до псевдоожижения, а значит, гидравлическое сопротивление неподвижного слоя в результате должно быть меньшим. Если после этого вновь начать псевдоожижение, то гистерезис уже не обнаруживается.

Таким образом, рабочая скорость w₀ потока в псевдоожиженном слое должна находиться в пределах w_пс < w₀< w_y . Отношение рабочей скорости к скорости начала псевдоожижения называют числом псевдоожижения К_п :

K_п= w₀ / w_пс .

Оно характеризует интенсивность перемешивания частиц. Для каждого конкретного процесса определяют оптимальное значение К_п , однако интенсивное перемешивание частиц обычно достигается уже при К_п=2.