3.4. Выпуклые множества и функции

Выпуклое множество. Подмножество Х векторного пространства У называется выпуклым, если для любых точек х , у  Х и числа  имеет место условие

Выпуклость множества имеет простую геометрическую интерпретацию: множество выпукло, если оно вместе с любыми двумя своими точками содержит и соединяющий их отрезок. Примерами выпуклых множеств являются евклидово пространство Е^п, любая гиперплоскость пространства Е^п, определяемая как

,

замкнутое полупространство в Е^п, определяемое как

,

и т.д. Если множества Х₁ и Х₂ выпуклы, то их пересечение Х₁  Х₂ и сумма Х₁ + Х₂ также выпуклы, однако их объединение Х₁  Х₂ может быть невыпуклым.

Пересечение конечного числа замкнутых полупространств есть выпуклое множество, называемое многогранным выпуклым множеством или выпуклым многогранником. Примером выпуклого многогранника (многогранного множества) является множество, определяемое как

,

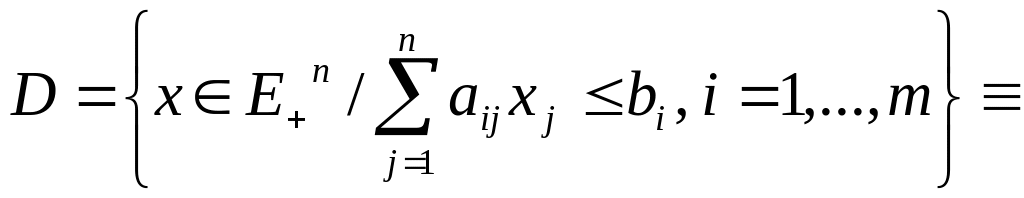
где А – (mxn) – матрица, содержащая коэффициенты {а_ij}, b – (mx1) - вектор, содержащий правые части {b_i}, Е₊^п – неотрицательный ортант пространства Е^п.

Многогранное множество (или многогранник) имеет вершины, боковые ребра, боковые грани. Когда оно неограниченно (по расстоянию), то имеет и экстремальные направления (боковые грани, уходящие в бесконечность). Количество вершин не превышает число C_n^m = n/m(n – m), а количество экстремальных направлений – число (n – m) C_n^m = n/m(n – m - 1).

Доказательство свойства выпуклости множества D весьма просто. Пусть . Рассмотрим точку Так как точки х¹ и х² неотрицательны и    , то х() Е₊^п, кроме того, она удовлетворяет условию

,

следовательно, точка х() удовлетворяет всем условиям, определяющим множество D, так что х()  D.

Весьма важным свойством многогранных множеств (многогранников) для современной теории оптимизации (теории экстремальных задач) является так называемая теорема о представлении. Ее сущность заключается в следующем. Пусть хⁱ, i = 1, …, k, - вершины D, а d ^j, j = 1, …, l, его экстремальные (или крайние) направления. Тогда любая точка х этого множества представляется в виде

х = ,

где _i   i, _i  1 _j  , j = 1, … , l. В частности, если множество D – ограниченное (по расстоянию) множество, тогда экстремальные направления отсутствуют, и условие представления приобретает форму х = Это условие означает, что любая точка ограниченного (по расстоянию) множества D единственным образом может быть представлена через его вершины. Согласно фундаментальной теореме математического программирования – теореме Вейерштрасса, - любая непрерывная функция достигает своего глобального максимума или минимума на ограниченном замкнутом множестве (в данном случае – выпуклом компакте).

Благодаря этому, любая линейная функция f(x) = с^Тх принимает свое наибольшее и наименьшее значения (свои максимумы и минимумы), по крайней мере в одной из вершин ограниченного многогранного множества, т.е.

f(xⁱ )  f(x)  f(x^j ),  x  D,

где xⁱ и x^j - вершины множества D. Именно на этом свойстве основано действие алгоритма симплекс - метода, который будет рассмотрен ниже в разделе линейного программирования.

Выпуклая комбинация. Выпуклой комбинацией точек (векторов) х¹, х², …, х^к называется точка (вектор) х, которую можно представить в виде

, , .

Крайняя точка. Крайней (или экстремальной) точкой выпуклого множества называется такой элемент этого множества, который не может быть представлен в виде выпуклой линейной комбинации двух различных его точек. У строго выпуклого множества все граничные точки являются крайними.

Выпуклая оболочка. Выпуклой оболочкой множества Х называется «наименьшее» выпуклое множество, содержащее Х, т.е. множество, являющееся пересечением всех выпуклых множеств, в которое входит Х. Выпуклое множество совпадает со своей выпуклой оболочкой.

Выпуклый многогранник. Выпуклая оболочка конечного числа точек в Е^п называется выпуклым многогранником – ограниченным многогранным выпуклым множеством. Выпуклый многогранник представляет собой множество всех выпуклых линейных комбинаций данных точек. Замкнутое ограниченное выпуклое множество есть выпуклая оболочка своих крайних точек.

Гиперплоскость. Если Х – выпуклое замкнутое множество в Е^п, а у - точка в Е^п, не принадлежащая Х, то существует ограничивающая гиперплоскость

H = {xEⁿ/ ,

содержащая у, такая, что все точки Х лежат в одном из замкнутых полупространств, определяемыми гиперплоскостью Н, т.е.

и либо ,

либо при любом z.

Выпуклая функция. Вещественная функция f(x), определенная на выпуклом множестве Х, называется выпуклой, если для любых двух различных точек x₁ , х₂ X и    имеет место условие

Если в этом определении неравенство выполняется как строгое, то функция называется строго выпуклой. Если функция f(x) выпуклая, то функция - f(x) является вогнутой. Аналогично определяется и строгая вогнутость функции. Ниже на рисунках приведено графическое изображение выпуклой и вогнутой функции скалярной переменной х. С геометрической точки зрения функция f(x), определенная на Е², выпукла, когда отрезок прямой, соединяющей любые две точки кривой ее графика, лежит не ниже данной кривой. Линейная функция является и выпуклой и вогнутой (но не в смысле строгой выпуклости или вогнутости).

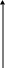а) график выпуклой функции б) вогнутая функция

f(x)

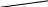
x₁

x₂

x

x₂

x₁

x

Рис.1.1. Графики выпуклой (слева) и

вогнутой (справа) функций.

Если вещественная функция f(x), определенная на выпуклом множестве Х, отвечает условию

, ,

при любых двух различных точках х и у из Х, то она называется квазивыпуклой, а функция - f(x) – квазивогнутой. При выполнении строгого неравенства говорят о строгой квазивыпуклости или квазивогнутости. Для квазивыпуклой функции характерно, что множество {x X / f(x)  b}, где b – любое вещественное число, является выпуклым.