
- •Теория вероятностей
- •§ 1. Предмет теории вероятностей
- •§ 2. Случайные события или исходы. Множество элементарных событий. Основные понятия
- •Примеры на построение множества ω.
- •Алгебраические операции над событиями
- •Диаграмма Венна.
- •Свойства операций
- •§ 3. Различные подходы к определению вероятности
- •П. 1. Аксиоматическое определение вероятности
- •П. 2. Классическое определение вероятности
- •Решение.
- •Решение.
- •Пп. 1. Комбинаторный метод вычисления вероятностей в классической схеме
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Пп. 2. Геометрические вероятности в классической схеме
- •Решение.
- •П. 3. Статистическое определение вероятности
- •§ 4. Основные теоремы теории вероятностей п.1. Теоремы сложения вероятностей
- •Доказательство.
- •Доказательство (методом математической индукции).
- •Доказательство.
- •Доказательство.
- •Решение.
- •Д оказательство (геометрическое)
- •П.2. Теоремы умножения вероятностей
- •Доказательство.
- •Решение.
- •Решение.
- •§ 5. Формулы полной вероятности и формула Байеса п. 1. Формула полной вероятности (следствие обеих основных теорем сложения и умножения)
- •Решение.
- •П. 2. Формула Байеса (Бейеса) (следствие теоремы умножения и формулы полной вероятности)
- •Решение.
- •§ 6. Последовательность независимых испытаний п. 1. Независимые испытания
- •П. 2. Формулы Бернулли.
- •Решение.
- •Решение.
- •Замечания.
- •Решение.
- •П. 3. Предельные теоремы в схеме Бернулли
- •Решение.
- •Решение.
- •Доказательство.
- •Решение.
- •П. 4. Наивероятнейшее число появления события в независимых испытаниях
- •Решение.
- •§ 7. Случайные величины п. 1. Основные определения
- •П. 2. Законы распределения случайных величин. Законы распределения дискретных случайных величин. Функция распределения
- •Формы закона распределения дсв.
- •Решение.
- •Решение.
- •3. Функция распределения – универсальный закон распределения (для дсв и нсв).
- •Свойства f(X).
- •Доказательство.
- •Графики функции распределения.
- •Решение.
- •Решение.
- •П. 3. Плотность распределения вероятностей нсв
- •Свойства плотности распределения
- •2. Условие нормировки: интеграл в бесконечных пределах от плотности распределения равен 1: . (4) Доказательство
- •Решение.
- •Решение.
- •П. 4. Числовые характеристики случайных величин, их роль и назначение
- •Пп 1. Характеристики положения (математическое ожидание, мода, медиана)
- •1. Математическое ожидание или среднее значение случайной величины
- •2. Мода случайной величины
- •3. Медиана случайной величины
- •Пп 2. Моменты
- •Доказательство.
- •И эксцесс
- •Решение.
- •Решение.
- •Решение.
- •П. 5. Законы распределения вероятностей дискретных случайных величин: биномиальный, Пуассона, гипергеометрический. Пп 1. Биномиальное распределение
- •Решение.
- •Пп 2. Распределение Пуассона
- •Решение.
- •Решение.
- •Пп 3. Гипергеометрическое распределение
- •Решение.
- •П. 6. Законы распределения вероятностей непрерывных случайных величин: равномерный, показательный, нормальный Пп 1. Равномерное распределение или закон равномерной плотности
- •Решение.
- •Пп 2. Показательное или экспоненциальное распределение
- •Решение.
- •Пп 3. Нормальный закон распределения
- •Смысл параметров m и σ
- •Решение.
- •§ 8. Системы случайных величин или случайные векторы п. 1. Основные понятия.
- •П. 2. Законы распределения свдт и свнт
- •Закон. Таблица распределения – закон распределения свдт.
- •Решение.
- •Решение.
- •Закон. Функция распределения – закон распределения свдт и свнт.
- •Решение.
- •3. Плотность распределения (для свнт)
- •Решение.
- •Решение.
- •П. 4. Плотности распределения отдельных величин, входящих в систему. Равномерное и нормальное распределения. Условные законы распределения
- •Решение.
- •Решение.
- •П. 5. Числовые характеристики системы. Корреляция. Линии регрессии
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •§ 9. Закон больших чисел. Предельные теоремы теории вероятностей
Решение.
Общее число исходов опыта – число всех
4-ех буквенных слов в данном опыте, а
именно:
![]() .
.
Событие А = {наудачу составленное слово из 4-х букв оканчивается на букву «а»}. Место буквы «а» - четвертое, оно занято, то есть число элементов множества А равно числу способов разместить на 3 оставшиеся первые места по одной букве из оставшихся 9. Следовательно, число исходов, благоприятствующих событию А, равно
![]()
Тогда вероятность события А равна
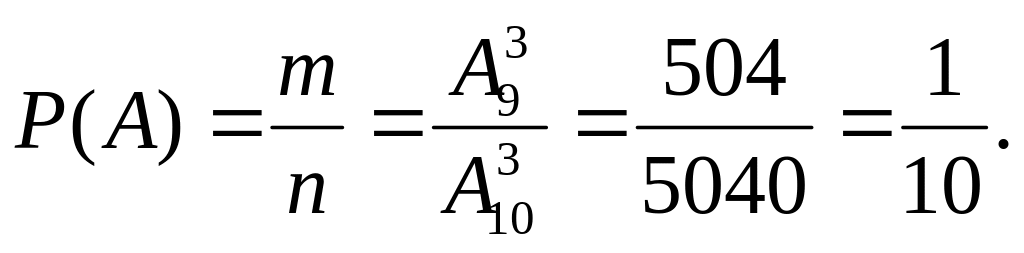
Пример 2. Из ящика, содержащего 10 перенумерованных изделий, наугад вынимают одно за другим все находящиеся в нем изделия. Найти вероятность того, что номера вынутых изделий будут идти по порядку: 1, 2,…, 10.
Решение.
Общее число исходов опыта – вариантов
расставить 10 изделий на 10 мест- равно
перестановке
![]()
Число исходов, благоприятствующих
событию В = {номера вынутых изделий
будут идти по порядку}, равно
![]()
Тогда вероятность события В равна
![]()
Пример 3 (на 1 и 2 схему). Из колоды из 36 карт вытащили наудачу 3 карты. Какова вероятность того, что они все будут тузы а) без учета порядка, б) с учетом порядка?
Решение.
а) Событие А = {вытащили 3 туза
без учета порядка}. Общее число исходов
опыта равно n
=![]() Число исходов, благоприятствующих
событию А, равно
Число исходов, благоприятствующих
событию А, равно
![]() Вероятность события
Вероятность события

б) Событие В = {вытащили 3 туза с
учетом порядка}. Общее число исходов
опыта равно n
=![]() Число исходов, благоприятствующих
событию В, равно
Число исходов, благоприятствующих
событию В, равно
![]() Вероятность события
Вероятность события
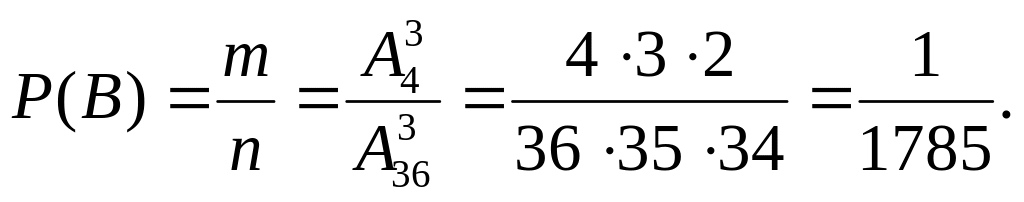
Схема выбора, приводящая к сочетаниям с повторениями
Пусть опыт состоит в выборке m неразличимых элементов из n наудачу с возвращением, но без последующего упорядочивания. Различными исходами опыта будут всевозможные m – элементные наборы, отличающиеся составом. При этом отдельные наборы могут содержать повторяющиеся элементы. Например, если m =4, то наборы ω1 = {l1, l2, l1, l1} и ω2 = {l2, l1, l1, l1} для эксперимента неразличимы, а набор ω3 = {l1, l3, l1, l1}- отличен от предыдущих.
Комбинации, получающиеся в результате
опыта, называются сочетаниями с
повторениями. Их общее число определяется
по комбинаторной формуле
![]() .
.
Пример. В библиотеке имеются книги по 16 разделам науки. Поступили 4 заказа на литературу. Считая, что любой состав литературы равновозможен, найти вероятности событий: а) А = {заказаны книги из разных разделов науки}, б) В = {заказаны книги из одного и того же раздела}.
Решение.
Число всех исходов равно числу сочетаний
с повторениями из 16 элементов по 4:
![]() .
.
а) Число исходов, благоприятствующих
событию А, равно числу способов
отобрать без возвращения 4 элемента из
16:
![]() Тогда вероятность события А равна
Тогда вероятность события А равна
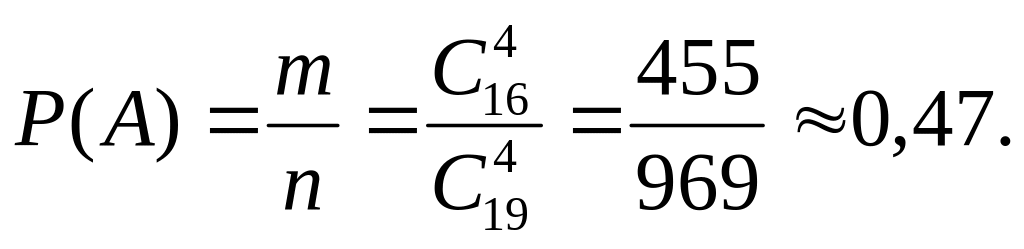
б) Число исходов, благоприятствующих
событию В, равно числу способов
отобрать без возвращения 1 элемент из
16:
![]() Тогда вероятность события В равна
Тогда вероятность события В равна
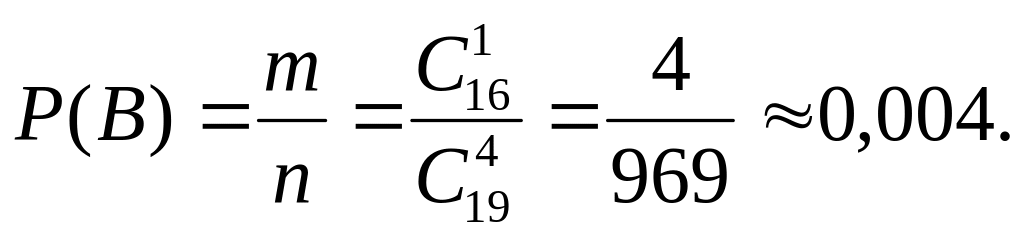
Схема выбора, приводящая к размещениям с повторениями
Пусть опыт состоит в выборке m элементов из n наудачу с возвращением и с упорядочиванием их в последовательную цепочку. Различными исходами будут всевозможные m – элементные наборы с повторениями, отличающиеся либо составом элементов, либо порядком их следования. Например, если m =4, то наборы ω1 = {l1, l2, l1, l1} и ω2 = {l2, l1, l1, l1} для эксперимента различимы. На одно место может претендовать несколько элементов.
Получаемые комбинации называются
размещениями с повторениями. Их общее
число определяется по комбинаторной
формуле
![]() .
.
Замечание.
а) Эту схему называют размещением по ячейкам: m различных элементов размещаются по n различным ячейкам.
б) Если в ячейку с номером i
попадают ровно mi
элементов, где i = 1,
2,…, n; m1
+ m2 +… +mn
= m, то число всех
размещений равно
![]() .
.
в) Бывают комбинации элементов из
различных групп. Пусть имеется m
групп элементов. Первая группа содержит
n1 различных
элементов, вторая - n2
элементов, …., последняя m-ая
- nm
элементов. Составляются комбинации
из m элементов
таким образом, что в каждую комбинацию
входит лишь по одному элементу из каждой
группы. Число всех комбинаций такого
типа равно
![]() .
.
Пример 1. Из ящика, содержащего 10 перенумерованных изделий, наугад вынимают одно за другим все находящиеся в нем изделия, записывают его номер, а затем выкладывают обратно и перемешивают с другими. Найти вероятность того, что записанные номера будут идти по порядку.
