
- •Теория вероятностей
- •§ 1. Предмет теории вероятностей
- •§ 2. Случайные события или исходы. Множество элементарных событий. Основные понятия
- •Примеры на построение множества ω.
- •Алгебраические операции над событиями
- •Диаграмма Венна.
- •Свойства операций
- •§ 3. Различные подходы к определению вероятности
- •П. 1. Аксиоматическое определение вероятности
- •П. 2. Классическое определение вероятности
- •Решение.
- •Решение.
- •Пп. 1. Комбинаторный метод вычисления вероятностей в классической схеме
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Пп. 2. Геометрические вероятности в классической схеме
- •Решение.
- •П. 3. Статистическое определение вероятности
- •§ 4. Основные теоремы теории вероятностей п.1. Теоремы сложения вероятностей
- •Доказательство.
- •Доказательство (методом математической индукции).
- •Доказательство.
- •Доказательство.
- •Решение.
- •Д оказательство (геометрическое)
- •П.2. Теоремы умножения вероятностей
- •Доказательство.
- •Решение.
- •Решение.
- •§ 5. Формулы полной вероятности и формула Байеса п. 1. Формула полной вероятности (следствие обеих основных теорем сложения и умножения)
- •Решение.
- •П. 2. Формула Байеса (Бейеса) (следствие теоремы умножения и формулы полной вероятности)
- •Решение.
- •§ 6. Последовательность независимых испытаний п. 1. Независимые испытания
- •П. 2. Формулы Бернулли.
- •Решение.
- •Решение.
- •Замечания.
- •Решение.
- •П. 3. Предельные теоремы в схеме Бернулли
- •Решение.
- •Решение.
- •Доказательство.
- •Решение.
- •П. 4. Наивероятнейшее число появления события в независимых испытаниях
- •Решение.
- •§ 7. Случайные величины п. 1. Основные определения
- •П. 2. Законы распределения случайных величин. Законы распределения дискретных случайных величин. Функция распределения
- •Формы закона распределения дсв.
- •Решение.
- •Решение.
- •3. Функция распределения – универсальный закон распределения (для дсв и нсв).
- •Свойства f(X).
- •Доказательство.
- •Графики функции распределения.
- •Решение.
- •Решение.
- •П. 3. Плотность распределения вероятностей нсв
- •Свойства плотности распределения
- •2. Условие нормировки: интеграл в бесконечных пределах от плотности распределения равен 1: . (4) Доказательство
- •Решение.
- •Решение.
- •П. 4. Числовые характеристики случайных величин, их роль и назначение
- •Пп 1. Характеристики положения (математическое ожидание, мода, медиана)
- •1. Математическое ожидание или среднее значение случайной величины
- •2. Мода случайной величины
- •3. Медиана случайной величины
- •Пп 2. Моменты
- •Доказательство.
- •И эксцесс
- •Решение.
- •Решение.
- •Решение.
- •П. 5. Законы распределения вероятностей дискретных случайных величин: биномиальный, Пуассона, гипергеометрический. Пп 1. Биномиальное распределение
- •Решение.
- •Пп 2. Распределение Пуассона
- •Решение.
- •Решение.
- •Пп 3. Гипергеометрическое распределение
- •Решение.
- •П. 6. Законы распределения вероятностей непрерывных случайных величин: равномерный, показательный, нормальный Пп 1. Равномерное распределение или закон равномерной плотности
- •Решение.
- •Пп 2. Показательное или экспоненциальное распределение
- •Решение.
- •Пп 3. Нормальный закон распределения
- •Смысл параметров m и σ
- •Решение.
- •§ 8. Системы случайных величин или случайные векторы п. 1. Основные понятия.
- •П. 2. Законы распределения свдт и свнт
- •Закон. Таблица распределения – закон распределения свдт.
- •Решение.
- •Решение.
- •Закон. Функция распределения – закон распределения свдт и свнт.
- •Решение.
- •3. Плотность распределения (для свнт)
- •Решение.
- •Решение.
- •П. 4. Плотности распределения отдельных величин, входящих в систему. Равномерное и нормальное распределения. Условные законы распределения
- •Решение.
- •Решение.
- •П. 5. Числовые характеристики системы. Корреляция. Линии регрессии
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •§ 9. Закон больших чисел. Предельные теоремы теории вероятностей
П. 2. Законы распределения случайных величин. Законы распределения дискретных случайных величин. Функция распределения
Для описания случайной величины (т.е. для возможности сказать, как часто следует ожидать появления тех или других возможных значений случайной величины в результате повторения опыта в одних и тех же условиях) необходимо знать закон распределения вероятностей случайной величины.
Определение 33. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Рассмотрим дискретную случайную величину (ДСВ) X с возможными значениями x1, x2, x3,…, xn. Каждое из этих значений возможно, но не достоверно, и X может принять каждое из них с некоторой вероятностью.
В результате опыта величина X примет одно из этих значений, т.е. произойдет одно из полной группы несовместных событий: X = х1 или X = х2 или … X = хn.
Обозначим Р(X = х1) = р1 , Р(X = х2) = р2 , …, Р( X = хn) = рn . Т.к. несовместные события образуют полную группу, то
![]() – сумма вероятностей всех возможных
значений ДСВ.
– сумма вероятностей всех возможных
значений ДСВ.
Эта суммарная вероятность каким-то образом распределена между отдельными значениями ДСВ. Задать это распределение, т.е. указать, какой вероятностью обладает каждое из событий, значит установить закон распределения СВ.
Говорят, что СВ подчинена данному закону распределения.
Формы закона распределения дсв.
1. Простейшей формой задания закона распределения является таблица, называемая рядом распределения ДСВ.
xi |
x1 |
x2 |
… |
xn |
pi |
р1 |
p2 |
… |
pn |
Для элементов нижней строки должно выполняться условие: .
2. Формой задания закона распределения является многоугольник распределения – фигура, получаемая при графическом изображении ряда распределения.
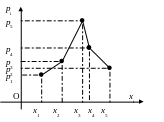
Возможные значения откладываются по оси (Ох). Вероятности возможных значений откладываются по оси (Oy).
Механическая интерпретация ряда распределения ДСВ: Распределение единичной массы в нескольких изолированных точках по оси (Ох). (В отдельных точках х1 , х2, …,хn сосредоточены соответственно массы р1, р2 , …, рn , сумма которых равна 1.)
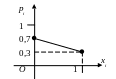
Пример 1. Рассмотрим опыт, в котором может появиться или не появиться событие А. Р(А) = 0,3. Рассмотрим случайную величину Х – число появлений события А в данном опыте, т.е. возможные значения данной величины: х1 = 0 (А не появится), х2 = 1 (А появится). Построить ряд распределения и многоугольник распределения случайной величины Х.
Решение.
Р(X = х1 = 0) = р1 =1 – 0,3 = 0,7, Р(X = х2 = 1) = р2 = 0,3.
xi |
0 |
1 |
pi |
0,7 |
0,3 |
Проверка:
![]() .
.
Пример 2. Стрелок производит 3 выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. За каждое попадание стрелку засчитывается 5 очков. Построить ряд и многоугольник распределения числа выбитых очков.
