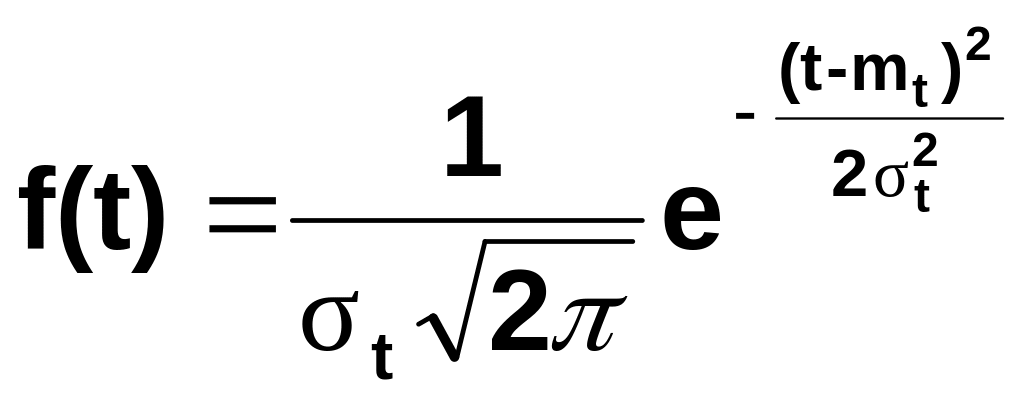3.2. Связь показателей надёжности с функциями распределения
Применительно к надёжности теплоэнергетических объектов в качестве СВ рассматривается время t. Соответственно вероятность отказа представляет собой вероятность того события, что фактическое время исправной работы объекта t' примет значение меньше заданного t, т.е. g(t) = P(t' < t). Это выражение является интегральной функцией распределения случайной величины t, что позволяет записать
g(t) = F(t). (37)
Соответственно, исходя из второго следствия теоремы сложения вероятностей противоположных событий ( p(t) + g(t) = 1) для вероятности безотказной работы объекта имеем
p(t) = 1- F(t). |
(37) |
Поскольку при неограниченном увеличении t функция вероятности отказа g(t) = F(t) стремится к 1, то обратная функция вероятности безотказной работы p(t) = 1 - F(t) стремится к 0, как это показано на рис 8.
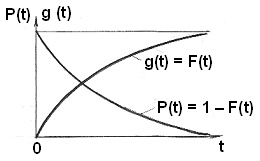
Рис.8. График зависимости вероятностей безотказной работы p(t) и отказа g(t) объекта от наработки t
Если закон распределения случайной величины t задан в виде дифференциальной функции распределения f(t), то вероятность отказа за наработку t находится интегрированием этой функции в интервале от 0 до t
|
(38) |
Поскольку пределами
изменения t являются 0 и ∞, то
.
Таким образом, зная конкретный вид и аналитическое выражение функции распределения исследуемой случайной величины t можно рассчитать вероятности g(t) и p(t) для любой требуемой наработки.
3.3.Сведения о законах распределения
Наиболее часто для характеристики надёжности теплоэнергетического оборудования и их систем используются экспоненциальный и нормальный законы распределения.
Экспоненциальный закон описывается дифференциальной функцией распределения вероятностей вида
|
(39) |
где mt - математическое ожидание; t - текущая переменная.
Среднеквадратичное отклонения СВ, распределяемой по этому закону, приблизительно равно её математическому ожиданию, т.е. σt ≈ mt.
Интегральная функция экспоненциального закона находится следующим образом
|
(40) |
.Нормальный закон описывается дифференциальной функцией распределения вероятностей вида
|
(41) |
Рабочую область функции принято ограничивать пределами t = mt ± 3σt, т.к. вероятность отклонения случайной величины t за эти пределы пренебрежительно мала.
Интегральная функция нормального закона распределения описывается формулой
F(t) = Фo(z1) + Ф(z2), |
(42) |
где z – интеграл вероятности Лапласа-Гаусса при z = (t – mt)/σt. Характерные виды кривых законов распределения CВ приведены на рис 9.
.
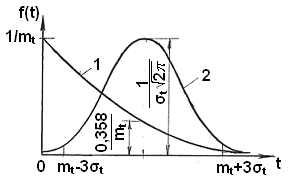
Рис. 9. Кривые дифференциальных функций при экспоненциальном (1) и нормальном (2) законах распределения
При оценках надёжности приведенные законы распределения применимы к конкретным техническим объектам. Так, экспоненциальному закону подчиняются объекты, для которых характерны внезапные отказы, а нормальному – объекты, теряющие работоспособность постепенно в результате износа. В качестве математического ожидания m при этом может служить наработка на отказ Тo.