Наибольший общий делитель. Наименьшее общее кратное.
1. Наибольший общий делитель (НОД) нескольких натуральных чисел - наибольшее натуральное число, на которое все эти числа делятся.
2. Наименьшее общее кратное (НОК) нескольких натуральных чисел - наименьшее натуральное число,кратное всем этим числам.
Вычисление НОК и НОД.
Ч
тобы
найти НОК (или НОД) нескольких чисел,
следует разложить на простые множители
каждое из чисел, затем вычислить
произведение
Н
общих
простых
множителей, взяв каждый из них с
наименьшим
показателем
степени, с которым он входит в данные
числа.
всех
простых
множителей, взяв каждый из них с
наибольшим
показателем
степени, с которым он входит в данные
числа.
ОК
Н
О Д
Пример
Найдем НОД и НОК чисел 720 и 1000
Р
720=2∙2∙2∙2∙3∙3∙5; 1000=2∙2∙2∙5∙5∙5.
азложим на простые множители каждое из чисел:
НОД(720;1000)=
2∙2∙2∙5=40.
НОК(720;1000)
= 2∙2∙2∙2∙ 3∙3∙ 5∙5∙5=73000
Взаимно простые числа.
Натуральные числа называются взаимно простыми, если их наибольший общий делитель равен 1.
НОК(а;в)∙НОД(а;в)=а∙в
Десятичные дроби.
Основные определения.
1.
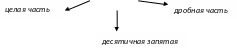2
3
,
56
Цифры дробной части называют десятичными знаками.
!!! Десятичная дробь не изменится, если в конце ее дописать или отбросить несколько нулей.
2. Чтобы записать десятичной дробью число, знаменатель дробной части которого есть разрядная единица, надо
записать целую часть числа и поставить запятую;
записать числитель дробной части, в которой предварительно количество цифр уравнено с количеством нулей в знаменателе.
Разрядный состав десятичных дробей:
Единицы миллионов |
Сотни тысяч |
Десятки тысяч |
Единицы тысяч |
Сотни |
Десятки |
Единицы |
Десятые |
Сотые |
Тысячные |
Десятитысячные |
Стотысячные |
Миллионные |
Десятимиллионные |
Стомиллионные |
Миллиардные |
Десятичная дробь |
|
|
|
|
|
1 |
2 |
4 |
2 |
|
|
|
|
|
|
|
12,42 |
|
|
|
|
7 |
- |
5 |
4 |
- |
2 |
|
|
|
|
|
|
705,402 |
|
|
|
6 |
8 |
- |
- |
- |
2 |
7 |
9 |
|
|
|
|
|
6800,0279 |
|
|
1 |
- |
- |
- |
1 |
4 |
- |
9 |
- |
3 |
2 |
|
|
|
10001,409032 |
|
3 |
5 |
- |
4 |
9 |
5 |
- |
- |
4 |
1 |
- |
4 |
7 |
|
|
350495,0041047 |
1 |
3 |
5 |
7 |
9 |
- |
2 |
4 |
6 |
8 |
- |
1 |
4 |
7 |
9 |
|
1357902,46801479 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9999999,999999999 |
3. Правило перевода обыкновенной дроби в десятичную.
1 способ
числитель обыкновенной дроби разделить на ее знаменатель
2 способ
используем основное свойство дроби, умножая числитель и знаменатель на одно и тоже число, чтобы в знаменателе получались числа кратные 10
3. !!! а) Если число умножается на неправильную дробь, результат больше множимого или равен ему;
б) Если число умножается на правильную дробь, результат меньше множимого.
п/п |
Название действия |
Что делаем? |
Примеры. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
сравнение десятичных дробей |
сравниваем поразрядно, начиная с наивысшего разряда. |
31,3494>31,34 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
сложение дробей |
|
1
13,83
14,15
27,98
2
)
4,3800
3,1472
7,5272
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
вычитание дробей |
|
1
13,80
4,15
9,65
2
)
345,8900
79,9002
265,9898 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 |
умножение дробей на 10, 100, 1000 и т.д. |
нужно перенести десятичную запятую вправо на столько знаков, сколько нулей имеется в записи числа, на которое умножаем |
56,7∙10=567 2,34∙1000=2340 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 |
умножение дробей на 0,1; 0,01; 0,001 и т.д. |
тоже, что и деление на 10, 100, 100 и т.д. (см п.7) |
5,67∙0,1=5,67:10=0,567 5,67∙0,01=5,67:100=0,0567 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6 |
умножение дробей |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7 |
деление дробей на 10, 100, 1000 и т.д. |
нужно перенести десятичную запятую влево на столько знаков, сколько нулей имеется в записи того числа, на которое делим |
56,7:100=0,567 56,7:10 000=0,00567 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8 |
деление дробей на 0,1; 0,01; 0,0001 и т.д. |
тоже, что и умножение на 10, 100, 100 и т.д. (см п.4 ) |
2,34:0,1=2,34∙10=23,4 2,34:0,001=2,34∙1000=2340 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9 |
деление дробей на натуральное число |
как деление натурального числа на натуральное, а десятичную запятую в частном ставят сразу, как только закончится деление целой части |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
10 |
деление дробей на десятичную дробь |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
)
)
0,579
,36154