Различные случаи ненормализованных мантисс

Разряды мантиссы	Величина мантиссы	Действия, выполняемые для нормализации результата
01, хх…х	Мантисса больше либо равна единице	Сдвиг мантиссы вправо на один разряд, увеличение порядка на единицу
10, хх…х
0 0,00…0хх…х k - разрядов	Модуль мантиссы меньше 1/2	Сдвиг мантиссы влево на k разрядов, уменьшение порядка на k единиц
1 1,11…1хх…х k – разрядов

Схема алгоритма сложения чисел с плавающей запятой представлена на рис. 4.2. В ней использованы обозначения: n – количество разрядов мантиссы, k – число разрядов порядка, М₁, М₂ – мантиссы и Р_1, Р₂ – порядки чисел.

Сложение мантисс выполняется на сумматоре мантисс SmM и возможно только при одинаковых порядках чисел. В связи с этим сначала нужно выровнять порядки, для чего на сумматоре порядков SmP определяется разность

Δ Р = Р₁ – Р₂. Если ΔР = 0, то порядки равны (P₁ = Р₂) и возможно сложение мантисс. При ΔР>0 первое число больше второго, и мантисса второго числа должна быть сдвинута на ΔР разрядов вправо. В случае ΔР<0 второе число больше первого. Следовательно, для выравнивания порядков необходимо сдвинуть на |ΔР| разрядов вправо мантиссу первого числа. Если |ΔР| превосходит количество цифровых разрядов, то в качестве результата операции сложения принимается большее число.

При нахождении разности порядков может иметь место переполнение результата (SmP). Если переполнение положительное, то в качестве результата сложения должен быть принят первый операнд. Отрицательное переполнение сумматора порядков свидетельствует о том, что в качестве результата сложения должен быть принят второй операнд.

Рис. 4.2. Схема алгоритма сложения чисел с плавающей запятой

Рис. 4.2. Схема алгоритма сложения чисел с плавающей запятой

(окончание)

После выполнения сложения мантисс может получиться денормализованный результат. При нормализации результата меняется величина порядка. Также может иметь место переполнение сумматора порядков. В случае положительного переполнения результат считается бесконечностью, знак которой определяется знаком мантиссы. При отрицательном переполнении сумматора порядков считается, что получен бесконечно малый результат, заведомо отличный от нуля, если мантисса не равна нулю.

Поскольку при выравнивании порядков мантисса меньшего из чисел сдвигается вправо, то имеет место потеря ее цифровых разрядов. В этом случае сумма чисел получается с недостатком, и для исключения накопления ошибок вычислений производится округление, для чего в сумматор вводится дополнительный младший разряд, к которому после выполнения операции сложения добавляется единица.

4.3. Проектирование алгоритма умножения чисел

Операция умножения чисел, представленных в форме с плавающей запятой, сводится к сложению их порядков, перемножению мантисс и, при необходимости, нормализации результата. При этом может иметь место денормализация результата не более чем на один разряд вправо. Нормализация производится по правилам табл. 4.1.

При сложении порядков операндов, а также при изменении порядка результата во время нормализации мантиссы произведения может произойти переполнение сумматора порядков, которое трактуется так же, как и при выполнении операции сложения.

Одним из распространенных способов перемножения мантисс чисел с плавающей запятой (или чисел с фиксированной запятой) является умножение младшими разрядами вперед. Для того чтобы автоматически получать правильный знак результата, удобно использовать дополнительные коды.

Структурная схема алгоритма умножения чисел с плавающей запятой, представленных модифицированным дополнительным кодом, младшими разрядами вперед приведена на рис. 4.3, где введены обозначения: М₁, Р₁ – мантисса и порядок множимого, М₂, Р₂ – мантисса и порядок множителя, n – число разрядов в множителе, два из которых в модифицированном коде являются знаковыми.

Для получения произведения мантисс выполняется (n-2) одинаковых цикла (по числу цифровых разрядов множителя), каждый из которых содержит два такта:

1) к содержимому сумматора прибавляется множимое, если младший разряд множителя равен единице;

2) содержимое регистра множителя и сумматора сдвигается вправо на один разряд (сдвиг выполняется модифицированный: в левом знаковом разряде значение сохраняется).

Поскольку перемножаются дополнительные коды, для получения правиль­ного результата при отрицательном множителе произведение должно быть скоррек­тировано. Это объясняется тем, что отрицательный множитель В^- в цифровых

Рис. 4.3. Схема алгоритма умножения чисел

разрядах содержит величину (1 – В^-). После выполнения (n-2) циклов на сумматоре будет получена величина

C = A × В^- = А (1 – В^-) = А – АВ^-,

в которой истинное произведение представлено слагаемым АВ^-. Следовательно, в ((n-2)+1)-м цикле к сумматору необходимо прибавить величину (-А). Далее производится округление результата путем добавления единицы к (n+1)-му разряду сумматора.

После округления выполняется сложение порядков. Примененные в алгоритме рис. 4.3 принципы нормализации мантиссы и анализа возможного переполнения сумматора порядков описаны выше.

4.4. Разработка алгоритма ускоренного умножения с обработкой

за один такт трех разрядов множителя

Получение произведения двух n-разрядных сомножителей традиционными алгоритмами, как правило, требует выполнения (n-2)+1 циклов (n-2 циклов для получения цифровой части произведения и один цикл для округления). В компьютерах, где преобладает выполнение операции умножения, целесообразно использовать ускоренные алгоритмы получения произведения чисел: с анализом групп нулей и единиц или с обработкой за один такт нескольких разрядов множителя.

Метод умножения с обработкой за один такт трех разрядов множителя является одним из самых быстрых логических методов ускорения выполнения операции умножения. Алгоритм (рис. 4.4) такого умножения чисел, представленных в форме с плавающей запятой, в данном случае будет отличаться от алгоритма, представленного в п. 4.3, только в той части, где производится умножение мантисс.

Как и любой из неускоренных алгоритмов, данный алгоритм (рис. 4.4) требует выполнения двух тактов в каждом цикле. В первом такте каждого цикла в зависимости от значений анализируемых разрядов множителя в сумматоре должна выполняться арифметическая операция в зависимости от сочетания очередной тройки разрядов (табл. 4.2). Во втором такте регистр множителя и сумматор сдвигаются на три разряда вправо. Количество выполняемых циклов равно (n-2)/3. Если в последнем цикле в знаковую пару разрядов множителя возник перенос, то нужен еще один цикл, в котором присутствует только первый такт, затем при необходимости вносится поправка в результат и производится округление.

Дальнейшие действия, связанные со сложением порядков и анализом переполнения сумматора порядков, идентичны соответствующим действиям алгоритма умножения п. 4.3.

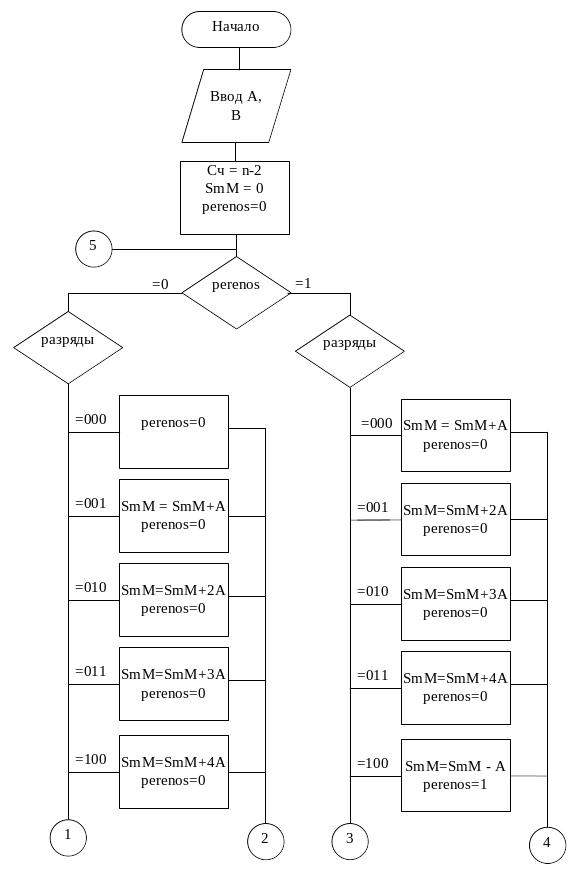
Рис. 4.4. Схема алгоритма ускоренного умножения с анализом за один такт трех разрядов множителя

Рис. 4.4. Схема алгоритма ускоренного умножения с анализом за один такт трех разрядов множителя (окончание)

Таблица 4.2

Зависимость выполняемой операции от разрядов множителя

Разряды множителя			Перенос из предыдущей пары разрядов	Перенос в следующую пару разрядов	Выполняемая операция
n-2	n-1	n
0	0	0	0	0	нет операции
0	0	1	0	0	+ А
0	1	0	0	0	+ 2А
0	1	1	0	0	+ 3А
1	0	0	0	0	+ 4А
1	0	1	0	1	- 3А
1	1	0	0	1	- 2А
1	1	1	0	1	- А
0	0	0	1	0	+ А
0	0	1	1	0	+ 2А
0	1	0	1	0	+ 3А
0	1	1	1	0	+ 4А
1	0	0	1	1	- 3А
1	0	1	1	1	- 2А
1	1	0	1	1	- А
1	1	1	1	1	нет операции

Проиллюстрируем примером выполнение операции ускоренного умножения чисел, представленных с плавающей запятой. Умножим младшими разрядами вперед числа А и В в дополнительных кодах методом ускоренного умножения с анализом за один такт трех разрядов множителя.

[М_А]_пр = 1,101101110 [P_A]_пр = 1,010

[М_В]_пр = 1,100010111 [P_В]_пр = 0,101

Так как производится операция умножения, то порядки чисел складываются.

[M_A]_доп = 11,010010010 = P₂ [P_A]_доп = 11,110

[M_B]_доп = 11,011101001 = P₁ [P_B]_доп = 00,101

[P_С]_доп = 00,011

Для выполнения ускоренного умножения нужно заранее подготовить значения 2*P₂, 3*P₂, 4*P₂, -P₂, -2*P₂, -3*P₂:

2P₂ = 10,100100100 - P₂ = 00,101101110

3P₂ = 01,110110110 - 2P₂ = 01,011011100

4P₂ = 01,001001000 - 3P₂ = 10,001001010

См = 000,000000000 0 P₁ = 11,011.101.001 перенос=0

⁺111,010010010 0

I 1) См=См+Р₂ = 111,010010010 0

2) См=См→³ = 111,111010010 0 перенос=0

⁺010,001001010 0

II 1) См=См-3P₂= 010,000011100 0

2) См=См→³ = 000,010000011 1 перенос=1

⁺101,001001000 0

III 1)См=См+4Р₂=101,011001011 1

2) См=См→³ = 111,101011001 0 перенос=0

⁺000,101101110 0

IV См=См – Р₂= 000,011000111 0 – поправка (так как В<0)

⁺000,000000000 1 – округление

[М_C]= 00,011000111

Ответ: С = 0,011000111 х 0,011.