Образец решения типового варианта

Задача 1. Предприятие производит продукцию трех видов и продает ее в трех регионах. Матрица задает цену реализации единицы продукции в i-том регионе по j-тому виду продукции. Матрица B – выручка предприятия в i-ом регионе по всем видам продукции (i = 1, 2, 3). Найти объем продаж по каждому виду продукции, если в каждый регион направляется одинаковое количество продукции каждого вида.

Указание: полученную систему линейных уравнений решить тремя способами:

1) по формулам Крамера;

2) матричным способом;

3) методом Гаусса.

Решение. Введем матрицу-столбец

,

где – объем продаж по i-тому виду продукции в каждом регионе (i = 1, 2, 3). Тогда для матриц А, В, Х справедливо соотношение

или

Это матричное уравнение равносильно системе линейных уравнений (СЛУ)

1 способ.

Решим эту СЛУ по формулам Крамера

.

Найдем

,

,

,

.

Тогда

,

,

.

Ответ: .

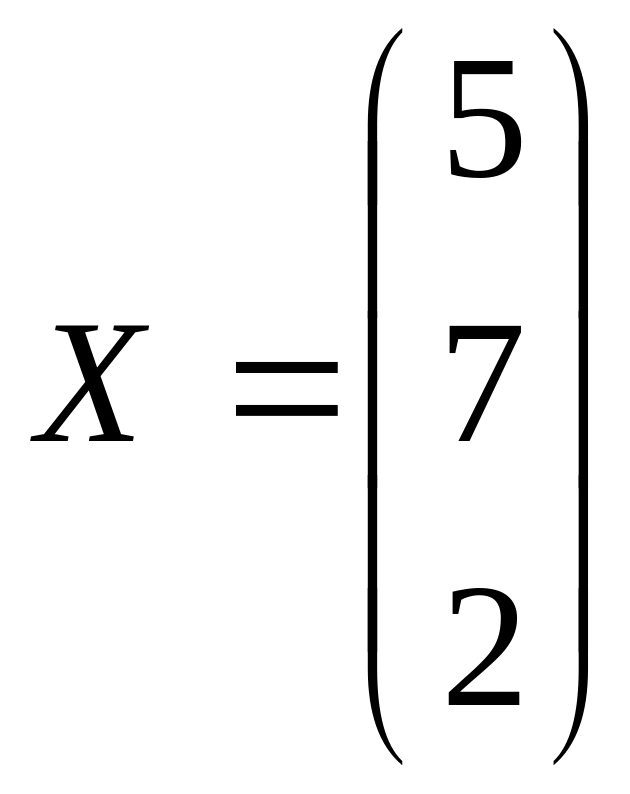2 способ.

Решим эту СЛУ матричным способом: .

Тогда

.

Найдем матрицу :

.

; ;

; ;

; ;

;

.

Матрица имеет вид:

.

Тогда решение СЛУ найдем по формуле

.

Ответ: .

3 способ.

Решим СЛУ методом Гаусса.

Ответ:

Как видим, ответы при решении СЛУ тремя способами совпали!

Задача 2. Некоторая кривая задана уравнением

.

Привести уравнение к каноническому виду, определить вид кривой и построить ее график.

Решение.

В левой части уравнения выделим полные квадраты по переменным х и у:

Разделим обе части уравнения на 4:

Полученное уравнение соответствует каноническому уравнению гиперболы с центром в точке :

.

У нас .

Ох – действительная ось, Оу – мнимая ось.

График гиперболы изображен на рисунке 1.

у

1

0. х

–2

Рисунок 1

Задача 3. Построить на плоскости ХОУ область решений системы линейных неравенств

Решение.

Построим прямые в системе ХОУ:

где числа в знаменателях дробей показывают отрезки, отсекаемые этими прямыми на соответствующих осях координат (рисунок 2).

у

10

х + у =10

3,75

х + 4у = 10

0 1,4 10 15 х

5х – 2у = 7

Рисунок 2

Задача 4. Провести полное исследование и построить график функции .

Решение.

1. ОДЗ: х ≠ 3, х (– ∞; 3) (3; +∞).

х = 3 – точка разрыва, значит х = 3 – вертикальная асимптота графика функции.

Исследуем поведение функции вблизи найденной асимптоты:

.

2. Четность, нечетность.

,

функция не является четной, функция

функция не является нечетной, общего вида.

3. Интервалы монотонности и точки экстремума.

Покажем на схеме (рисунок 3).

max min

+ – – +

0 3 6 x

Рисунок 3

4.Выпуклость, вогнутость, точки разрыва.

– +

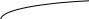
3 x

Рисунок 4

5. Асимптоты.

y = kx + b – уравнение наклонной асимптоты.

k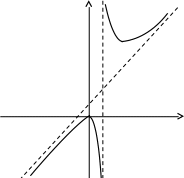 = = 1.

b = = = .

– наклонная асимптота.

6. Пересечение с осями координат: с осью Оу: x = 0, y = 0.

Значит, график функции проходит через начало координат.

Построим график заданной функции (рисунок 5).

у

–3 0 3 х

Рисунок 5

Задача 5. Дана функция: . Показать, что функция удовлетворяет уравнению:

. (*)

Решение.

1) Найдём частные производные первого порядка.

= = =

.

2) Найдём частные производные второго порядка.

3) Подставим частные производные второго порядка в уравнение (*).

.

Получили тождество, поэтому функция удовлетворяет заданному уравнению.

Задача 6. Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной заданными параболой , прямой и осью Ох.

Решение.

Найдем координаты точек пересечения параболы и прямой:

2 x² = –3x + 4,

2 x² + 3 x – 4 = 0,

x₁ = 1/2,

x₂ = –2.

Рисунок 6

Объем V_ox находим по формуле:

Ответ:

Задача 7. Вычислить несобственный интеграл или доказать его расходимость.

.

Решение.

По определению, получаем:

интеграл сходится.

Ответ: интеграл сходящийся.

Задача 8. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям:

Решение.

Покажем, что уравнение является линейным:

xy′ + 2y = 6x⁴ (: x)

y′ + 2 = 6x³,

т.е. соответствует y′ + P(x)y = Q(x) – линейное дифференциальное уравнение первого порядка.

Пусть y = u∙v,

y′ = u′∙v + u∙v′,

u′∙v + u∙v′ + 2 = 6x³,

v∙(u′ + ) + u∙v′ = 6x³.

Разобьем полученное уравнение на два:

1) u′ + = 0, 2) u∙v′ = 6x³,

u′ = – , ∙v′ = 6x³,

= – , v′ = 6x⁵,

= – , = 6x⁵,

ln = –2ln , = ,

u = . v = x⁶ + c.

y = u∙v = = x⁴ + – общее решение.

Начальные условия x = 1, y = 1. Подставим в общее решение.

1 = 1 + c c = 0. Это значение записываем в общее решение.

y = x⁴ – решение задачи Коши (частное решение).

Задание 9. Найти общее решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами:

y′′ – y′ = 9xe^2x.

Решение.

Составим однородное дифференциальное уравнение, отбросив правую часть:

y′′ – y′ = 0.

Составим характеристическое уравнение и найдем его корни:

k² – k = 0,

k (k – 1) = 0,

k₁ = 0 или k₂ = 1.

Тогда имеем решение:

y_одн.= С₁e^0x + С₂e^x = С₁ + С₂e^x.

Для нахождения y* выпишем правую часть заданного уравнения:

f(x) = 9xe^2x = P₁(x)∙ , = 2 ≠ k_1,2.

y* = e^2x(A₀ + A₁x), где A₀, A₁ – необходимо найти.

Т.к. y* – решение, предполагаемое для заданного дифференциального уравнения, то эта функция должна удовлетворять заданному дифференциальному уравнению:

(y*)′ = 2e^2x(A₀ + A₁x) + A₁e^2x,

(y*)′′ = 4e^2x(A₀ + A₁x) + 2A₁e^2x + 2A₁e^2x = 4e^2x(A₀ + A₁x) + 4A₁e^2x.

Подставим найденные производные в заданное уравнение:

4e^2x(A₀ + A₁x) + 4A₁e^2x – (2e^2x(A₀ + A₁x) + A₁e^2x) = 9xe^2x, (:e^2x)

4(A₀ + A₁x) + 4A₁ – (2(A₀ + A₁x) + A₁) = 9x,

2A₁x + 3A₁ + 2A₀ = 9x.

Многочлены в разных частях уравнения будут равны, если коэффициенты при одинаковых степенях x совпадут:

x: 2A₁ = 9, A₁ = ,

x⁰: 3A₁ + 2A₀ = 0, A₀ = .

Решение y* имеет вид:

y* = e^2x .

Общее решение заданного уравнения:

y = y_одн. + y* = С₁ + С₂e^x + e^2x .

Задание 10.ариант №30.ание 1: ____________________ Исследовать сходимость числового ряда . Решение.

– знакоположительный ряд.

Применяем интегральный признак сходимости (признак Коши). Пусть .

– несобственный интеграл с бесконечным верхним пределом (первого рода)

Несобственный интеграл является сходящимся.

– сходится.

Ответ: – сходится.

Задание 11. Найти область сходимости степенного ряда .

Решение.

Здесь общий член ; тогда ; .

Вычислим радиус сходимости:

Искомый степенной ряд сходится для . ;

;

.

Исследуем сходимость ряда на концах интервала сходимости. Пусть , тогда:

Ряд расходится, так как не имеет суммы. Следовательно, – точка расходимости.

Пусть , тогда:

Ряд расходится, так как не имеет суммы. Следовательно, – точка расходимости.

Ответ: заданный ряд сходится для .